coursera-斯坦福-机器学习-吴恩达-第1周笔记

coursera-斯坦福-机器学习-吴恩达-第1周笔记

0 前言

第一，这门课是最好的机器学习、深度学习入门教程之一，老师很有名气，是深度学习三驾马车之一的吴恩达，而且课程讲的很通俗易懂。

每堂课后面还有编程作业，一定要做。课程推荐使用Octave编程语言，只需要填写核心代码，很适合自学。这门语言很多人没有学过，有些排斥。但是学计算机的同志就是要保持对新事物新工具的热爱，更何况这门语言并不难。

第二，我发现网络上关于这门课的笔记有很多，但是质量参差不齐。有的虎头蛇尾甚至半途而废；有的几乎就是复制英文讲义，没有自己的理解。这也是我写笔记的目的，顺便强化自己的理解。

第三，这门课有官方笔记，自己下载下来，有条件的打印出来。用笔实际写写画画理解会更深刻，比如我的。

[外链图片转存失败(img-xQxVCtOZ-1566960874849)(http://oqy7bjehk.bkt.clouddn.com/17-12-6/86302226.jpg)]

1 Introduction介绍-对应笔记lectur

1 Introduction介绍-对应笔记lecture1

1.1 机器学习应用

这一章首先简单介绍了，机器学习在现实生活中用的应用例子。吹了一波机器学习未来应用宏伟蓝图，好像又回到大学教室听老师吹牛的感觉~

1.2 机器学习概念

介绍了机器学习的概念：A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

主要包括了几个名词：你要做的任务T；以往可以学习经验的数据记录E；和判别记录做对否的判别器P

1.3 机器学习分类

1. 监督学习 Supervised learning （已知经验数据E的对错标签“p”）

• 1.1 回归 regression（连续值）
• 1.2 分类 classification（离散值）

2. 非监督学习 Unsupervised learning（有以往数据，但不知道他们的分类）

• 2.1 聚类 clustering
• 2.2 非聚类 non-clustering

2 一个变量的线性回归 -对应lecture2

这一节对应官方笔记lecture2。

2.1 线性回归的表示

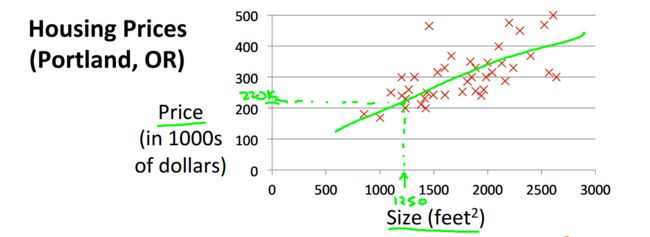
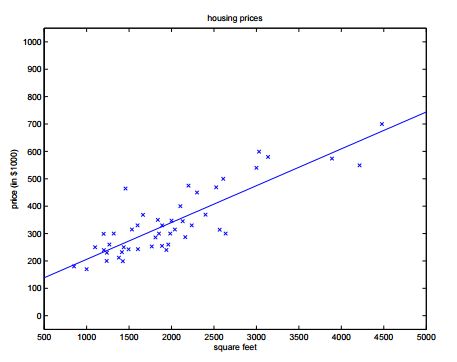
起始给出了预测房价的例子。 像这样用一条线来模拟房价走势，就叫做线性回归。

这个问题属于监督问题，每个样本都给出了准确的答案。
同时因为房价是连续值，所以这是一个回归问题，对给定值预测实际输出。

公式：

$h_{\theta }(x)={\theta }_0+{\theta }_1\ast x$

其中两个θ是位置参数，我们的目的是求出他俩的值。

2.2 Cost function 代价函数

我们取怎样的θ值可以使预测值更加准确呢？

想想看，我们应使得每一个预测值hθ和真实值y差别不大，可以定义代价函数如下

$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{\left({\hat{y}}_i-y_i\right)}^2=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x_i)-y_i\right)}^2$
这样，只需要通过使J值取最小，即可满足需求

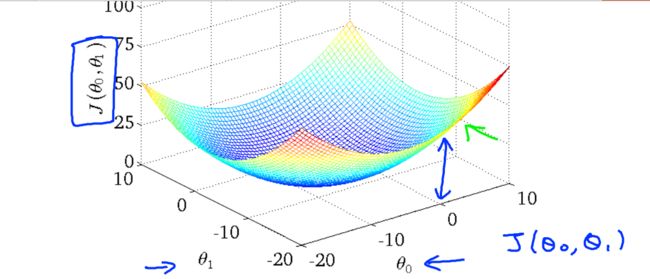
那么怎么使J最小化呢？看图：误差与两个参数的关系。

我们看到通过改变斜线的斜率 误差变得很小。也就是选择了右图的中心圈子里。

2.3 参数求解（❤梯度下降法❤）

从上图，我们直观的看到，圈子中心误差最小。那么怎样从数学的角度计算得到那个“中心点”呢？老师给的方法是“梯度下降”

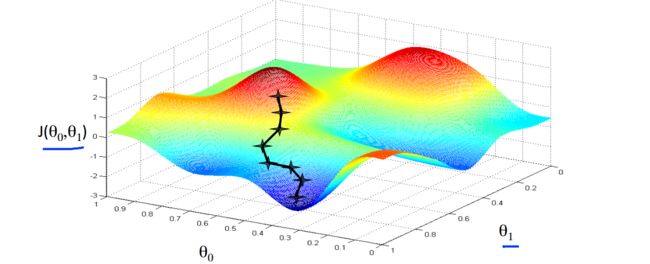
如图，当我们的成本函数处于图的坑底时，即当它的值是最小值时，我们将知道我们已经成功了。

红色箭头显示图中的最小点。我们这样做的方式是通过我们的成本函数的导数（函数的切线）。切线的斜率是那个点的导数，它会给我们一个走向的方向。我们降低成本功能的方向与最陡的下降。每一步的大小由参数α决定，称为学习率。

公式如下：

$\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0, \theta_1) $
重复计算这个公式，直到函数收敛。

注意更新theta值应同时更新

其中的α称之为步长，在最优化课中我们有好几种方法来确定这个α的值。

这个α如果过小，则收敛很慢；如果过大，则可能导致不收敛。

对于J(θ)的偏导数学推导过程如下：

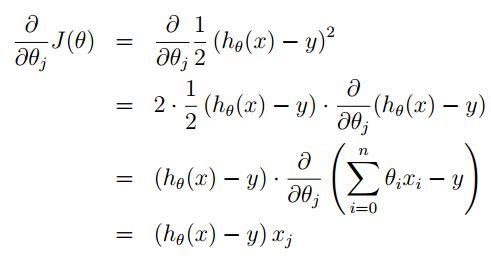
在这里你就看到，我们在构造J(θ)时1/2的出现就是为了与指数的在求导时抵消。 经过简单的替换之后我们就可以得到θ新的迭代公式：

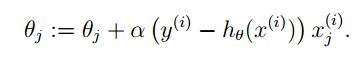
2.4 总结

到这里，我们就学习了一个最最简单的机器学习模型求解的全部内容。我们梳理一下，一共有三个层次 的 三个公式。

1. 第一层 模型函数
   $h_{\theta }(x)={\theta }_0+{\theta }_1\ast x$

2. 第二层 代价函数
   $J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x_i)-y_i\right)}^2$

3. 第三层 GD法求解参数
   $\theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0, \theta_1) $

就这么简单 ，就可以求出一个预测房价的线性回归模型。

3 线性代数知识复习 -对应lecture3

3.1 概念

线性代数知识，主要理解“向量”和“矩阵”两个概念即可。
[外链图片转存失败(img-THMjQzTn-1566960874858)(https://dn-anything-about-doc.qbox.me/document-uid49570labid2865timestamp1493280416377.png)]

a是一个3×2的矩阵，b是一个2×3的矩阵，c是一个3×1的矩阵，d是一个1×2的矩阵。

其中，c只有一列，我们也可以称c为列向量，d只有一行，我们也可以称d为行向量。本课程中，对于向量，默认都是指列向量。

3.2 矩阵运算

1. 矩阵的数乘运算

一个标量（你可以直接理解为一个数字）乘以矩阵，得到的结果为矩阵中的每个元素和该标量相乘，如下
[外链图片转存失败(img-1FNesTnp-1566960874859)(https://dn-anything-about-doc.qbox.me/document-uid49570labid2865timestamp1493281897854.png)]

2. 矩阵的转置运算

转置运算通过在矩阵右上角添加一“撇”表示。
[外链图片转存失败(img-0MLq1uTw-1566960874860)(https://dn-anything-about-doc.qbox.me/document-uid49570labid2865timestamp1493281947905.png)]

3. 矩阵之间的加减法

矩阵之间的加减法要求参与运算的两个矩阵尺寸相同，运算的结果等于两个矩阵对应元素相加
[外链图片转存失败(img-GL4FTnqR-1566960874860)(https://dn-anything-about-doc.qbox.me/document-uid49570labid2865timestamp1493282210391.png)]

4. 矩阵魔力的来源–矩阵之间的乘法

用第一个矩阵的行元素，乘第二个矩阵的列元素。所以矩阵乘法首先要求参与乘法运算的两个矩阵的尺寸能够“兼容”，具体的要求就是，第一个矩阵的列数与第二个矩阵的行数必须相同。

[外链图片转存失败(img-sYZdSCPo-1566960874861)(https://dn-anything-about-doc.qbox.me/document-uid49570labid2865timestamp1493282455569.png)]