数据结构之树和二叉树

树型结构是一类重要的非线性数据结构，树是以分支关系定义的层次结构。

树（Tree）

树是n（n>=0）个结点的有限集。

在任意一棵非空树中：

（1）有且仅有一个特定的根结点（Root）

（2）当n>1时，其余节点可分为m（m>0）个互不相交的有限集，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）

一些相关的基本术语：

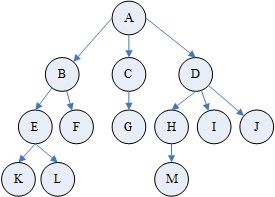
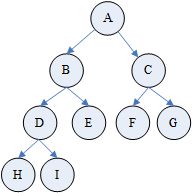
（1）度（Degree）：结点拥有的子树数称为结点的度。例如上图中A的度为3，C的度为1，F的度为0

（2）叶子（Leaf）或终端结点：度为0的结点。上图中的叶子结点有K,L,F,G,M,I,J

（3）树的度：树内各节点的度的最大值。上图中树的度为3

（4）孩子（Child）：结点的子树的根，相应的，该节点称为孩子的双亲（Parent）。

（5）兄弟（Sibling）：同一个双亲的孩子互称为兄弟。上图中的H,I,J互为兄弟。

（6）祖先：从根结点到该结点所经分支上的所有结点。例如M的祖先为A,D,H。反之，以某结点为根的子树中的任一结点都称为该结点的子孙。

（7）层次（Level）：从根开始定义，根为第一层，根的孩子为第二层。

（8）堂兄弟：双亲在同一层的结点。例如上图中的F,G

（9）树的深度（Depth）或高度：树中结点的最大层次称为树的深度。上图中树的深度为4

（10）森林（Forest）：是m（m>=0）棵互不相交的树的集合。

二叉树（Binary Tree）

二叉树是另一种树型结构，它的特点是每个节点至多只有两棵子树（即二叉树中不存在度大于2的结点）。

二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树的性质：

（1）在二叉树的第i层上，至多有个结点（i>=1）

（2）深度为k的二叉树至多有个结点（k>=1）

（3）对任何一棵二叉树T，如果其叶子结点树为，度为2的结点数为，则=+1

（4）具有n个结点的完全二叉树的深度为+1

（5）一棵有n个结点的完全二叉树的结点按层序编号，则对任一结点有：

（a）如果i=1，则结点i是二叉树的根，无双亲；若i>1，则其双亲是结点

（b）如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子为结点2i

（c）如果2i+1>n，则结点i无右孩子；否则其右孩子为结点2i+1

遍历二叉树（Traversing Binary Tree）

遍历二叉树即如何按某条搜索路径巡访树中每个结点，使得每个结点均被访问一次，而且仅被访问一次。

已知二叉树是由3个基本单元组成的：根结点，左子树，右子树。

假如以L,D,R分别表示遍历左子树，访问根结点和遍历右子树，若限定先左后右，则有3种情况：先序遍历、中序遍历、后序遍历

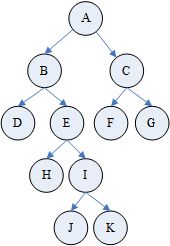
如上图的二叉树，其先序遍历结果为：ABDEHIJKCFG，中序遍历结果为：DBHEJIKAFCG，后序遍历结果为：DHJKIEBFGCA

线索二叉树（Threaded Binary Tree）

二叉链表作为存储结构时只能找到结点的左，又孩子信息，而不能直接得到结点在任一序列中的前驱和后继信息。为了保存这种信息，可以在二叉树节点上增加两个标志域。

其中：

指向结点前驱和后继的指针称为线索，加上线索的二叉树称之为线索二叉树。

对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。

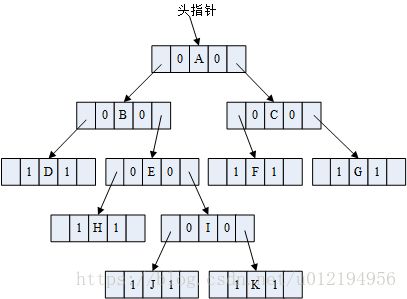
上图中的二叉树可以修改为以下线索链表：

二叉排序树（Binary Sort Tree）/二叉搜索树（Binary Search Tree,BST）/二叉查找树

二叉排序树或者是一棵空树，或者是具有以下性质的二叉树：

（1）若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值

（2）若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值

（3）它的左右子树也分别为二叉排序树

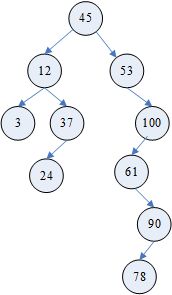
下图为一棵二叉排序树：

平衡二叉树（Balanced Binary Tree 或 Height-Balanced Tree）

平衡二叉树又称为AVL树。它或者为一棵空树，或者是具有以下性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

若将二叉树上结点的平衡因子BF（Balance Factor）定义为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有结点的平衡因子只可能是-1，0,1.

只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

完全二叉树（Complete Binary Tree）

若二叉树的深度为h，除第h层外，其他各层（1~h-1）的结点都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

假设是度为0的结点（叶子结点）总数，是度为1的结点总数，是度为2的结点总数，则这样的完全二叉树有如下性质：

（1）n=++

（2）n=1++2*

（3）=

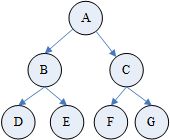
以下为一棵完全二叉树：

满二叉树（Full Binary Tree）

如果一棵二叉树的结点要么是叶子结点，要么有两个子结点，这样的树就是满二叉树。即一棵满二叉树的层数为k，且结点总数是-1.

下图为一棵满二叉树：