神奇的分形图像（一）-Fractal Image-Mandelbrot And Julia

• 分析学原理不做过多阐述：这里以举例子的方式加以阐述，更能通俗的理解其概念。

分形几何学是一门以不规则几何形态为研究对象的几何学

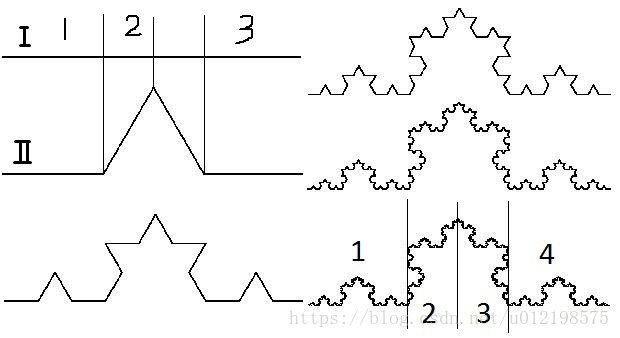
从上图，你能很清晰的回答出它们是直线、矩形、长方体、维度分别是1、2、3维

但是如下图形呢我们通常引入豪斯多夫维度来衡量该图像的维度

这张图像来源是：https://www.zhihu.com/question/19931652

可能你不好理解为什么是n^3 = 4，其实你可以想象成Ⅰ图变成Ⅱ图是

一、首先分割成均等的三分

二、将中间（1/3长度的直线）变成尖角（总长度2/3长度的直线）

所以3 * length（Ⅱ） = 4 * length（Ⅰ）

则 维度

• 今天要介绍的是Mandelbrot And Julia 曼德勃罗集 和 朱丽叶集 的代码实现

曼德勃罗集 和 朱丽叶集  都是利用 公式迭代

相同的是迭代初值均为 而不同的迭代的参数

曼德勃罗集选用继续迭代，而朱丽叶集采用固定参数迭代

其次需要理解一个知识点、迭代的条件是必须要收敛，否则结果无意义

这里参与迭代的参数是复数，如果对复数不了解请自行百度，复数表达方式为

定义迭代结束的条件是 等价于

其中flag = 0实现曼德勃罗集 flag = 1实现 朱丽叶集，参数c由滑条TrackBar调节。

#include 
#include 
#include 
using namespace cv;
using namespace std;
const int trackbar_val_max = 200;

class CMandelbrot
{
public:
	CMandelbrot(): x1(0), y1(), ScaleX(), ScaleY(),image(Mat()){}
	/*explicit CMandelbrot(int) : x1(0), y1(0), ScaleX(0), ScaleY(0)
	{}*/
	CMandelbrot(float x1,float y1,float ScaleX,float ScaleY, Mat image)
	{
		this->x1 = x1;
		this->y1 = y1;
		this->ScaleX = ScaleX;
		this->ScaleY = ScaleY;
		this->image = image;
	}
public:
	Mat   getImage(){return image;}
	float getX1(){return x1;}
	float getY1(){return y1;}
	float getScaleX(){return ScaleX;}
	float getScaleY(){return ScaleY;}
private:
	float x1;
	float y1;
	float ScaleX;
	float ScaleY;
	Mat image;
};
//逃逸时间算法实现
int mandelbrot(const complex &z0, const int max,const complex &z1)
{
	complex z = z0;

	for(int t = 0; t < max; t++)
	{
		if(z.real() * z.real() + z.imag() * z.imag()> 4.0f) return t;
		z = z * z + z1;
	}

	return max;
}
int mandelbrotFormula(const complex &z0,const complex &z1, const int maxIter=255) {
	int value = mandelbrot(z0, maxIter, z1);
	if(maxIter - value == 0)//if value == maxIter, set pixel = 0
	{
		return 0;
	}
	return cvRound(sqrt(value / (float) maxIter) * 255);// in order to overcome linear scaling is make no sense to change of gray
}
void sequentialManelbrot(Mat &img, const float x1, const float y1, const float scaleX, const float scaleY, complex & c = complex(0, 0) ,int flag = 0)
{
	if(flag == 0)
	{
		if(img.channels() == 1)
		{
			for(int i = 0; i < img.rows; i++)
			{
				for(int j = 0; j < img.cols; j++)
				{
					float x0 = j / scaleX + x1;//img x point convert to Mandelbrot set
					float y0 = i / scaleY + y1;//img y point convert to Mandelbrot set
					complex z0(x0,y0);
					uchar value = (uchar)mandelbrotFormula(z0,z0);
					img.ptr(i)[j] = value;

				}
			}
		}
		else
		{
			for(int i = 0; i < img.rows; i++)
			{
				for(int j = 0; j < img.cols; j++)
				{
					float x0 = j / scaleX + x1;//img x point convert to Mandelbrot set
					float y0 = i / scaleY + y1;//img y point convert to Mandelbrot set
					complex z0(x0,y0);
					uchar value = (uchar)mandelbrotFormula(z0,z0);
					if(value > 150)
						img.at(i, j) = Vec3b(0, 0, value);
					else if(value > 75)
						img.at(i, j) = Vec3b(0, saturate_cast(value + 75), saturate_cast(value+150));
					else if(value > 50)
						img.at(i, j) = Vec3b(0, value+50, 100);
					else if(value > 10)
						img.at(i, j) = Vec3b(value+25, value+50, 100);
					else if(value > 0)
						img.at(i, j) = Vec3b(value+25, 0, 100);
					else
						img.at(i, j) = Vec3b(0, 0, 0);
				}

			}
		}
	}
	else
	{
		if(img.channels() == 1)
		{
			for(int i = 0; i < img.rows; i++)
			{
				for(int j = 0; j < img.cols; j++)
				{
					float x0 = j / scaleX + x1;//img x point convert to Mandelbrot set
					float y0 = i / scaleY + y1;//img y point convert to Mandelbrot set
					complex z0(x0,y0);
					uchar value = (uchar)mandelbrotFormula(z0,c);
					img.ptr(i)[j] = value;

				}

			}
		}
		else
		{
			for(int i = 0; i < img.rows; i++)
			{
				for(int j = 0; j < img.cols; j++)
				{
					float x0 = j / scaleX + x1;//img x point convert to Mandelbrot set
					float y0 = i / scaleY + y1;//img y point convert to Mandelbrot set
					complex z0(x0,y0);
					uchar value = (uchar)mandelbrotFormula(z0,c);
					if(value > 150)
						img.at(i, j) = Vec3b(0, 0, value);
					else if(value > 75)
						img.at(i, j) = Vec3b(0, value, saturate_cast(value+150));
					else if(value > 50)
						img.at(i, j) = Vec3b(0, value, 50);
					else if(value > 10)
						img.at(i, j) = Vec3b(value+25, value, 50);
					else if(value > 0)
						img.at(i, j) = Vec3b(value+25, 0, 50);
					else
						img.at(i, j) = Vec3b(0, 0, 0);
				}

			}
		}

	}
	
}
static float CalibrateRate(int pos)
{
	float rate = pos * 1.0f /  trackbar_val_max;
	if(rate < 0.5)
		rate = -2 * rate;
	else
		rate = 2 * rate;
	return rate;
}
static void on_trackbar_Real(int pos, void * userdata)
{
	int im_pos = getTrackbarPos("imaginary", "fractal");
	CMandelbrot *mm = (CMandelbrot *)userdata;
	float re_rate = CalibrateRate(pos);
	float im_rate = CalibrateRate(im_pos);
#ifdef _DEBUG
	cout << "re_rate" << re_rate << endl;
	cout << "im_rate" << im_rate << endl;
#endif
	sequentialManelbrot(mm->getImage(),mm->getX1(),mm->getY1(),mm->getScaleX(),mm->getScaleY(),complex(re_rate,im_rate),1);
	imshow("fractal",mm->getImage());
}
static void on_trackbar_Imaginary(int pos , void * userdata)
{
	int re_pos = getTrackbarPos("real", "fractal");
	CMandelbrot *mm = (CMandelbrot *)userdata;
	float re_rate = CalibrateRate(re_pos);
	float im_rate = CalibrateRate(pos);
#ifdef _DEBUG
	cout << "re_rate" << re_rate << endl;
	cout << "im_rate" << im_rate << endl;
#endif
	
	sequentialManelbrot(mm->getImage(),mm->getX1(),mm->getY1(),mm->getScaleX(),mm->getScaleY(),complex(re_rate,im_rate),1);
	imshow("fractal",mm->getImage());
}
int main()
{
	namedWindow("fractal",1);
	Mat mandelbrotImg2(800,600,CV_8UC3);
	float x1 = -1.4f, x2 = 1.16f;
	float y1 = -1.2f, y2 = 1.2f;
	float scaleX = mandelbrotImg2.cols / (x2 - x1);
	float scaleY = mandelbrotImg2.rows / (y2 - y1);
	CMandelbrot mm(x1,y1,scaleX,scaleY,mandelbrotImg2);
	int re = 40,im = 40;
	createTrackbar("real","fractal",&re,trackbar_val_max,on_trackbar_Real,&mm);
	createTrackbar("imaginary","fractal",&im,trackbar_val_max,on_trackbar_Imaginary,&mm);
	waitKey();
}

实现结果

Re =  -0.4  Im = 0.65

调的颜色有点丑，大家请见谅。