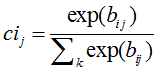Geoffrey Hinton《Dynamic Routing Between Capsules》阅读笔记
论文地址:https://arxiv.org/pdf/1710.09829v1.pdf
参考文章:
http://blog.csdn.net/uwr44uouqcnsuqb60zk2/article/details/78463687
(知乎)https://zhihu.com/question/67287444/answer/251460831
http://blog.csdn.net/zchang81/article/details/78382472
1 Capsule和Traditional Neuron的对比
首先,一张图展示Capsule和Traditional Neuron的异同:
论文使用了两层卷积神经网络,对原始黑白照片,也就是 28 * 28 * 8 的原始张量,用两层卷积,完成一系列张量变换,转变成新的张量 ( x_{attr, lon, lat, channel} ) ,attr = 0 ... 7, lon = 0 ... 5, lat = 0 ... 5, channel = 0 ... 31。
这个新张量中的 ( x_{attr} ) 是初级 capsule,表达原始图像中值得注意的特征。其中 attr 代表初级 capsule 的属性,维度为 8。
新张量中的 ( x_{lon, lat} ) 表示 capsule ( x_{attr} ) 在原始图像中的方位。经过张量变换后,28 * 28 的原始图像,被缩略为 6 * 6 个方位。( x_{channel} ) 是频道,类似于多机位拍摄同一个场景,全面表达 capsule 在原始图像中的视觉特点,总共有 32 个频道。
在新张量中,总共有 lon * lat * channel = 6 * 6 * 32 = 1152 个初级 capsule ( x_{attr} ) 。换句话说,经过一系列张量变换,从原始图像中,筛选出了 1152 个值得注意的图像特征,而每个特征是一个8维的向量。
高级 capsule 是前文说的十个手写体数字的 16 维属性向量,即 ( x_{attr, class} ), attr = 0 ... 15, class = 0 ... 9。
想识别原始图像中,是否包含手写体数字 3,也就是 class = 2,只需要把 1152 个初级 capsules,逐一与高级 capsule 向量 x_{*, 2} 做比对。
如何做比对呢?先做一次线性变换(仿射变换),把 8 维的初级 capsule,变换成 16 维的初级 capsule。然后计算 16 维的初级 capsule 与 16 维的高级 capsule 之间的余弦距离,也就是两个向量之间的点乘。
从每个高级 capsule 出发,在低级 capsules 中寻找它存在的证据,这个过程,就是 Dynamic Routing。
如果某一个高级 capsule 中每一个属性,都能在 1152 个初级 capsules 中,找到 “对应的” 一个或多个 capsules,那么就证实了高级 capsule 中的这个属性,确实在图像中存在。
如果某一个高级 capsule 中的全部 16 个属性,都能在 1152 个初级 capsules 中,找到存在的证据,那么就认定这个高级 capsule 在原始图像中存在。
如果有多个高级 capsules,都能在 1152 个初级 capsules 中,找到各自存在的证据,那么就认定在原始图像中存在多个高级 capsules,这也解释了Capsule对于识别重合的数字有较好效果的原因。
4 总结和展望
在过去30年的时间里,在语音识别方面最先进的方法一直使用具有高斯混合的隐马尔可夫模型作为输出分布。这种模型容易在小型计算机上学习,但它们有一个致命的缺陷:与使用分布式表示的循环神经网络相比,它们所使用的one-of-n表示策略是指数级低效率的。为了将隐马尔可夫可以记住的有关它所产生的字符串的信息量加倍,我们需要平方隐藏节点的数量;但对于循环(神经)网络,我们只需要将隐藏的神经元数量加倍即可。
当下,CNN网络在目标识别领域具有举足轻重的地位,所以探索算法中是否存在可能被替换的指数级低效率操作是有意义的。其中一个可能被替代的点就是卷积网络在泛化到新的图像视角(如仿射变换)下时具有难度。CNN应对图像平移的能力是内在的,但是对于放射变换中其它维度(放射变换包括平移、旋转、放大、缩小等维度)的变换,我们可以通过增加特征检测器(及卷积核个数)或者增加标注数据量的方式来解决这个问题,但这些方法都是指数级低效率的操作。Capsule通过将像素强度转换成已识别片段的实例化参数矢量,然后将转换矩阵应用于已识别片段以预测较大片段的实例化参数的方法避免了这些指数级的低效率操作。而学习编码部分和整体之间内在空间关系的变换矩阵构成了算法能自动推广到新视角的视角不变性知识。
Capsule做了非常强的代表性假设:在图像中的每个位置,最多只有一个Capsule代表的实体类型实例。这种由被称为“Crowding”的感知现象激发的假设消除了绑定问题,并允许Capsule使用分布式表示来编码该类型实体在给定位置的实例化参数。这种分布式表示比通过激活高维网格上的点来编码实例化参数指数地更高效,且该方法具有正确的分布式表示,然后Capsule就可以充分利用空间关系可以通过矩阵乘法来进行建模的事实来使算法对图像的仿射变换具有不变性。
Capsule使用随视点变化而变化的神经活动,而不是试图消除神经活动中的视点变化。这使得他们比等标准化方法更具有优势:它们可以同时处理不同对象或对象不同部分的多个不同仿射变换。
此外,Capsule在解决计算机视觉领域另一个困难问题——分割上表现良好,这是因为如我们在本文中所展示的那样,实例化参数的向量允许他们使用路由协议。Capsule的研究现状就类比于本世纪初递归神经网络在语音识别领域的应用研究阶段。目前已经有一些基本的实验表现表明这是一种更好的方法,但是在它能够超越目前已有高度发展的技术之前,还需要更多细微的洞察。
事实上,简单的Capsule系统在分割重叠数字方面已经取得了无可比拟的性能,这也是Capsule一个值得探索的方向的初期指引。