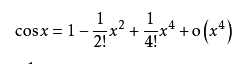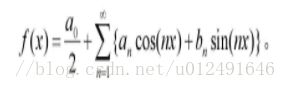高中数学角度看傅里叶变换
以下内容都是通过单维角度来看的
傅里叶公式推理
最初。认为任何一个周期函数都可以写成具有三角函数的形式
有段傅里叶在生前的故事,描述其猜想论文迟迟没有发表的过程。
直觉来说
函数可以展开泰勒公式
f(x) = 1 + f(x)'/1!*x + f(x)''/2!*x^2......
猜想
f(x) = 1+∑(a1*cos+a2*sin)
事实证明这是可以无限接近的一种表达方式
进入话题之前,我们还是需要有一定的三角式基础
例如 表达式
f = a sin(bx +c)
这里 a 代表的是三角函数的振幅(amplitude),b代表 频率 frequency ,c代表相位(相位就是水平平移的度量) ,为何不叫平量?
所以
sin(θ) 代表 振幅 为1 ,频率为1的三角函数
sin(2θ) ...频率为2的三角。
同时相位在傅里叶分析的作用并不是非常大,因为
f = a*sin(bx +c)= a*sin(bx) * cos(c)+a*cos(bx) * sin(c)
可以把a*cos(c) = a1 ,a*sin(c)= b1 为了求解,我们不必求出c是多少,a是多少,而只要
求出 a1,b1 就行 了,所以 f 也就直接写成
f = a1 * sin(bx) +b1 * cos(bx)
数学往往是用简单的代表复杂的事物,去理解事物
现在进入正题
傅里叶其实就是求解 振幅 频率的过程 (相位的作用不是很大,因为上面写到的公式,由一个正弦变成一个正弦加上一个余弦,余弦就是相位的另一种分解)
网上说傅里叶过程实质上是通过时域上的数据变成频域上的数据,这句话说得有些过于高大上,因为 时域是 啥,频域是啥,对于刚刚接触傅里叶信息处理的同学来说:相当于
让人解释 加法是什么的一个问题,很容易陷入自我解释并陷入死循环的过程。
其实用数学的语言,就是看上面的过程,f(x)就是所谓的时域数据,也就是这个f(x)是由时间组成的一连串时间序列数据列表
而频域数据就是 上式的右边式子中的 a0,a1.b1,a2,b2...... 对的这个就是振幅,换句话说频域就是代表了一种量的叠加,那么cos(nx),sin(nx)这些我们需要知道吗?其实,计算机
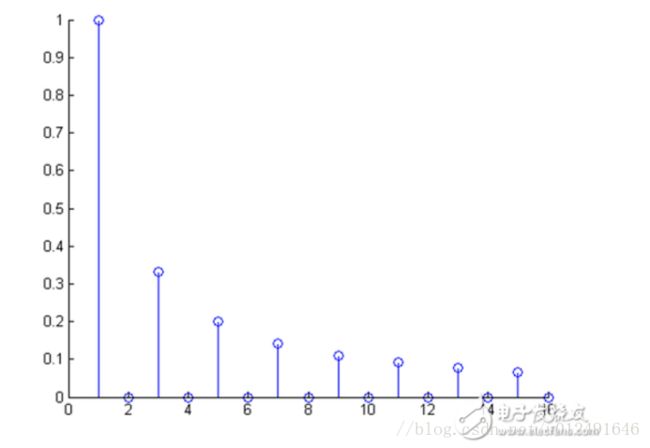
很喜欢做的就是枚举,在程序中 cos(nx),sin(nx) 中的 n 是从 【1 , 序列(长度)/2+1】这个长度变化的,当然你也可以扩大n的范围,但是理论上来说,n越大,相当于如下图
(窃取的图,。。。。)
圆圈越小,在数学上来说就是趋近于0,无穷小。所以,一般不考虑,我们只要找出能够近似的三角函数就算完成目标了。
一般算法最后会得到
一份频域图(知道这个频域指的是什么了吧)
上图
问题来了,傅里叶变换速度很慢,因为要遍历所有的数据集以及所有的频率n(1,n/2+1)
但是现实是残酷的,没那么多时间给你算,然后发明了fft (fast 傅里叶变换)
这个待看。
http://blog.csdn.net/linmingan/article/details/51194187
http://blog.csdn.net/u012363005/article/details/51868249
http://blog.sina.com.cn/s/blog_57ad1bd20100txgs.html
http://blog.csdn.net/It_BeeCoder/article/details/78565527
http://users.rowan.edu/~polikar/WAVELETS/WTpart1.html