数据结构之最小生成树
最小生成树: 一个连通图的生成树是一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的n-1条边。这种构造连通网的最小代价生成树称为最小生成树,详见数据结构之图(术语、存储结构、遍历)。
在所有u∈U、v∈V-U的边(u, v)∈E中找一条代价最小的边(u, vi)并入集合TE,同时将vi并入U,直至U=V为止。
此时TE中必有n-1条边,则T={V,{TE}}即为N的最小生成树。
需要用到两个辅助数组:
lowcost[MAX_VEM]:存储从U到V-U的具有最小代价边上的权——lowcost[i] = Min{w(u, vi)|u∈U,vi∈V-U}
adjvex[MAX_VEM]:存储从U到V-U的具有最小代价边(u,vi)依附在U中的顶点u的下标——adjvex[i] = {u|lowcost[i] }
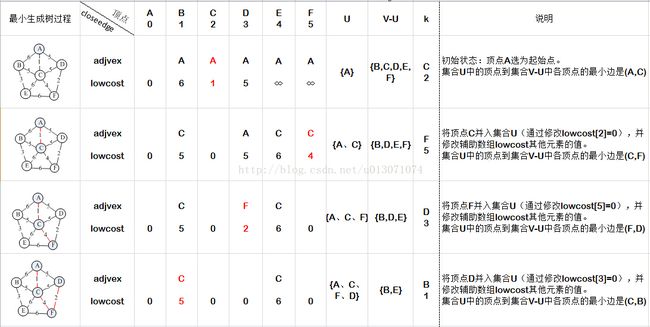
根据上述prime算法描述,求其最小生成树的过程如下:
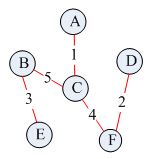
最后得到如下最小生成树:

数据结构(C语言版)
完整的测试代码:http://download.csdn.net/detail/u013071074/7467561
求连通网的最小生成树有两种经典方法:普里姆(Prime)算法和克鲁斯卡尔(Kruskal)算法。
1、Prime算法
(1)算法描述
假设N=(V,{E})是连通网,TE是N上最小生成树中边的集合。从V中任选一个顶点u0,算法从U={u0}(u0∈V),TE={}开始,重复执行以下步骤:在所有u∈U、v∈V-U的边(u, v)∈E中找一条代价最小的边(u, vi)并入集合TE,同时将vi并入U,直至U=V为止。
此时TE中必有n-1条边,则T={V,{TE}}即为N的最小生成树。
需要用到两个辅助数组:
lowcost[MAX_VEM]:存储从U到V-U的具有最小代价边上的权——lowcost[i] = Min{w(u, vi)|u∈U,vi∈V-U}
adjvex[MAX_VEM]:存储从U到V-U的具有最小代价边(u,vi)依附在U中的顶点u的下标——adjvex[i] = {u|lowcost[i] }
(2)实例
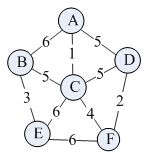
给定如下一个无向网:
根据上述prime算法描述,求其最小生成树的过程如下:
最后得到如下最小生成树:

(3)、算法代码
//普里姆(Prime)算法
void MiniSpanTree_Prime(Graph *g, VertexType u0)
{
int min, i, j, k, v0;
int adjvex[MAX_VEX]; //存储从U到V-U的具有最小代价边(u,vi)依附在U中的顶点u的下标
//adjvex[i] = {u|lowcost[i] = Min{w(u, vi)|u∈U,vi∈V-U}}
int lowcost[MAX_VEX]; //存储从U到V-U的具有最小代价边上的权——lowcost[i] = Min{w(u, vi)|u∈U,vi∈V-U}
v0 = k = LocateVex(g, u0); //定位开始的顶点u0在顶点数组中的下标号
assert(k != -1);
//adjvex[k] = k; //初始化第一个顶点下标为k
lowcost[k] = 0; //初始,U={u}
for (i = 0; i < g->vexNum; i++)
{
if (i != k) //初始化除下标为k的其余全部顶点
{
adjvex[i] = k; //初始化都为顶点u对应的下标k
lowcost[i] = g->arc[k][i]; //将顶点u与之有关的权值存入数组
}
}
for (i = 0; i < g->vexNum; i++)
{
if (i == v0)
{
continue;
}
min = INFINITY;
for (j = 0, k = 0; j < g->vexNum; j++)
{
if (lowcost[j] != 0 && lowcost[j] < min) //V-U中的全部顶点
{
min = lowcost[j];
k = j;
}
}
//printf("(%d,%d) ", adjvex[k], k); //打印当前顶点中权值最小的边:
//g->vexs[adjvex[k]]∈U,g->vexs[k]∈V-U
printf("(%c,%c) ", g->vexs[adjvex[k]], g->vexs[k]);
lowcost[k] = 0; //第k顶点并入U集
for (j = 0; j < g->vexNum; j++)
{
if (lowcost[j] != 0 && g->arc[k][j] < lowcost[j])
{
lowcost[j] = g->arc[k][j]; //新顶点并入U后重新选择最小边
adjvex[j] = k;
}
}
}
putchar('\n');
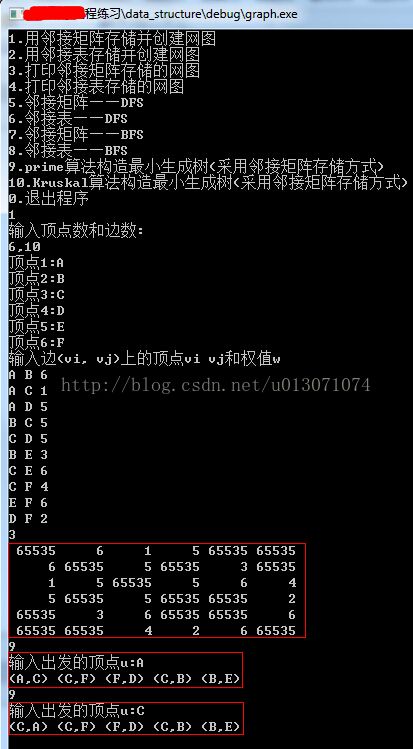
}运行截图:
分析:邻接矩阵实现的普里姆算法的时间复杂度为O(n^2),与网中的边数无关,适用于求边稠密的网的最小生成树。
2、Kruskal算法
(1)算法描述
假设连通网N={V,{E}},令最小生成树的初始状态为只有n个顶点而无边的非连通图T={V,{}},图中的每个顶点自成一个连通分量。在E中选择代价最小的边,若改边依附的顶点落在T中不同的连通分量上,则将次边加入到T中,否则舍去此边而选择下一条代价i最小的边。以此类推,直到T中所有顶点都在同一个连通分量上为止。Kruskal算法主要考虑是否会形成环路。在实际的代码编写中,一般采用边集数组这一数据结构:
//边集数组
#define MAX_EDGE 100 //最大边数
typedef struct
{
int begin;
int end;
EdgeType weight;
}Edge;我们可以通过程序将邻接矩阵通过程序转化为边集数组,并且对它们的按权值从小到大排序。如下图所示。
(2)算法代码
//将邻接矩阵结构转化成边集
void Convert(Graph *g, Edge edge[])
{
int i, j, k = 0;
for (i = 0; i < g->vexNum; i++)
for (j = i; j < g->vexNum; j++) //无向图的邻接矩阵是对称的
if (g->arc[i][j] < INFINITY)
{
edge[k].begin = i;
edge[k].end = j;
edge[k].weight = g->arc[i][j];
k++;
}
#if 0
printf("排序前:\n");
printf(" \tbeign\tend\tweight\n");
for(i = 0; i < k; i++)
{
printf("edge[%d]\t%d(%c)\t%d(%c)\t%d\n", i,
edge[i].begin, g->vexs[edge[i].begin],
edge[i].end, g->vexs[edge[i].end], edge[i].weight);
}
#endif
InsertSort(edge, k);
#if 1
printf("排序后:\n");
printf(" \tbeign\tend\tweight\n");
for(i = 0; i < k; i++)
{
printf("edge[%d]\t%d(%c)\t%d(%c)\t%d\n", i,
edge[i].begin, g->vexs[edge[i].begin],
edge[i].end, g->vexs[edge[i].end], edge[i].weight);
}
#endif
}
//按权值大小对边集数组edge从小至大排序
void InsertSort(Edge edge[], int k)
{
int i, j;
Edge tmp;
for (i = 1; i < k; i++)
{
if (edge[i].weight < edge[i - 1].weight)
{
tmp = edge[i];
for (j = i - 1; edge[j].weight > tmp.weight; j--)
{
edge[j + 1] = edge[j];
}
edge[j + 1] = tmp;
}
}
}
//查找连线顶点的尾部
int Find(int *parent, int f)
{
while(parent[f] > 0)
{
f = parent[f];
}
return f;
}
//克鲁斯卡尔算法实现
void MiniSpanTree_Kruskal(Graph *g)
{
int i, n, m;
Edge edges[MAX_EDGE]; //定义边集数组
int parent[MAX_EDGE]; //定义一数组用来判断边与边是否形成环
//将邻接矩阵转化为边集数组edges并按权值由小到大排序
Convert(g, edges);
for(i = 0; i < g->vexNum; i++)
{
parent[i] = 0; //初始化数组值为0
}
for(i = 0; i < g->arcNum; i++) //循环每一条边
{
n = Find(parent, edges[i].begin);
m = Find(parent, edges[i].end);
if(n != m) //假如n与m不等,说明此边没有与现有生成树形成环路
{
parent[n] = m; //将此边的结尾顶点放入下为起点的parent数组中
//表示此顶点已经在生成树集合中
//printf("(%d,%d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
printf("(%c,%c) ", g->vexs[edges[i].begin], g->vexs[edges[i].end]);
}
}
putchar('\n');
}运行截图:

不考虑邻接矩阵或邻接表转化为边集数组的时间开销,克鲁斯卡尔算法的Find函数由边数e决定,时间复杂度为O(loge),而外面有一个for循环e次,所以克鲁斯卡尔算法的时间复杂度为O(eloge),相对prime算法而言,适合于求边稀疏的网的最小生成树。
数据结构(C语言版)
完整的测试代码:http://download.csdn.net/detail/u013071074/7467561