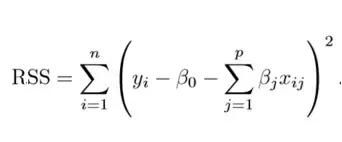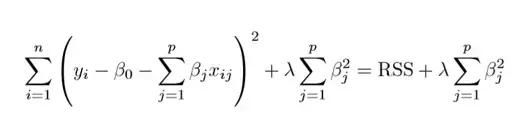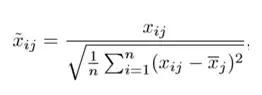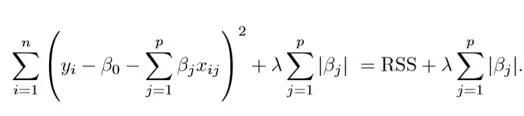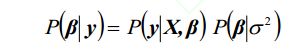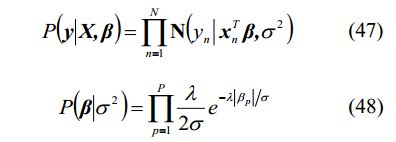Batch 、Batch_Size、weight decay、momentum、normalization和正则化的一些理解和借鉴

整理一下之前看过的内容，方便后面忘记时查询。

谈谈深度学习中的 Batch_Size

Batch_Size（批尺寸）是机器学习中一个重要参数，涉及诸多矛盾，下面逐一展开。

首先，为什么需要有 Batch_Size 这个参数？
Batch 的选择，首先决定的是下降的方向。如果数据集比较小，完全可以采用全数据集 （Full Batch Learning ）的形式，这样做至少有 2 个好处：其一，由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。其二，由于不同权重的梯度值差别巨大，因此选取一个全局的学习率很困难。 Full Batch Learning 可以使用Rprop 只基于梯度符号并且针对性单独更新各权值。

对于更大的数据集，以上 2 个好处又变成了 2 个坏处：其一，随着数据集的海量增长和内存限制，一次性载入所有的数据进来变得越来越不可行。其二，以 Rprop 的方式迭代，会由于各个 Batch 之间的采样差异性，各次梯度修正值相互抵消，无法修正。这才有了后来RMSProp 的妥协方案。

既然 Full Batch Learning 并不适用大数据集，那么走向另一个极端怎么样？
所谓另一个极端，就是每次只训练一个样本，即 Batch_Size = 1。这就是在线学习（Online Learning）。线性神经元在均方误差代价函数的错误面是一个抛物面，横截面是椭圆。对于多层神经元、非线性网络，在局部依然近似是抛物面。使用在线学习，每次修正方向以各自样本的梯度方向修正，横冲直撞各自为政，难以达到收敛。 

 

可不可以选择一个适中的 Batch_Size 值呢？
当然可以，这就是批梯度下降法（Mini-batches Learning）。因为如果数据集足够充分，那么用一半（甚至少得多）的数据训练算出来的梯度与用全部数据训练出来的梯度是几乎一样的。

批训练引入最大的好处是针对非凸损失函数（凸函数就是U型函数）来做的，毕竟非凸的情况下，全样本就算工程上的动，也会卡在局部最优上，批表示了全样本的部分抽样实现，相当于认为引入修正梯度上的采样噪声，使“一路不通找别路”更有可能的搜索最优值。

 

在合理范围内，增大 Batch_Size 有何好处？

• 内存利用率提高了，大矩阵乘法的并行化效率提高。
• 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
• 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。

盲目增大 Batch_Size 有何坏处？

• 内存利用率提高了，但是内存容量可能撑不住了。
• 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
• Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

训练：

若全集有502张图片，参数batch_size=30,则训练一次全集需要跑502/32=15次，epoch是训练全集的次数，epoch=100即训练100次全集。

调节 Batch_Size 对训练效果影响到底如何？
这里跑一个 LeNet 在 MNIST 数据集上的效果。MNIST 是一个手写体标准库，我使用的是 Theano 框架。这是一个 Python 的深度学习库。安装方便（几行命令而已），调试简单（自带 Profile），GPU / CPU 通吃，官方教程相当完备，支持模块十分丰富（除了 CNNs，更是支持 RBM / DBN / LSTM / RBM-RNN / SdA / MLPs）。在其上层有 Keras 封装，支持 GRU / JZS1, JZS2, JZS3 等较新结构，支持 Adagrad / Adadelta / RMSprop / Adam 等优化算法。 

运行结果如上图所示，其中绝对时间做了标幺化处理。运行结果与上文分析相印证：

• Batch_Size 太小，算法在 200 epoches 内不收敛。
• 随着 Batch_Size 增大，处理相同数据量的速度越快。
• 随着 Batch_Size 增大，达到相同精度所需要的 epoch 数量越来越多。
• 由于上述两种因素的矛盾， Batch_Size 增大到某个时候，达到时间上的最优。
• 由于最终收敛精度会陷入不同的局部极值，因此 Batch_Size 增大到某些时候，达到最终收敛精度上的最优。

       深度神经网络的优化是个nonconvex problem.所以基于SGD的训练batch size不能取过大。过大的batchsize的结果是网络很容易收敛到一些不好的局部最优点。。同样太小的batch也存在一些问题，比如训练速度很慢，训练不容易收敛等。。具体的batch size的选取和训练集的样本数目相关。。举个例子，比如在3小时的语音识别库（大约108万个样本）训练DNN,通常batch 取128..而在300小时的库上会取1024.

 

对weight decay、momentum和normalization的一些理解

一、weight decay（权值衰减）的使用既不是为了提高收敛精确度也不是为了提高收敛速度，其最终目的是防止过拟合。在损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大。

  这个式子在下面的正则化中会详细讲解，其中就是前面说的weight decay 

二、momentum是梯度下降法中一种常用的加速技术。

对于一般的SGD，其表达式为,沿负梯度方向下降。学习率

而带momentum项的SGD则写生如下形式：

其中即momentum系数，通俗的理解上面式子就是，如果上一次的momentum（即）与这一次的负梯度方向是相同的，那这次下降的幅度就会加大，所以这样做能够达到加速收敛的过程。

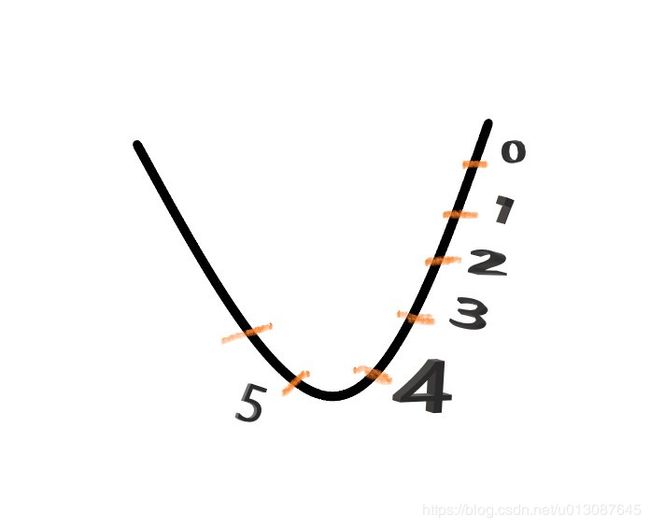
如上图所示，在刚开始的时候为0，也就是没有动量，从1到2时和从0到1的负梯度方向相同则这次的动量就会加大，就有可能到达3这样就会在下降方向加快收敛。若从4到5发现动量方向和从3到4不同则到达5的时候就会减弱梯度，减小摆动加快收敛。

三、batch normalization的是指在神经网络中激活函数的前面，将按照特征进行normalization，这样做的好处有三点：
1、提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。
2、提升学习速率。归一化后的数据能够快速的达到收敛。
3、减少模型训练对初始化的依赖。

 

L1和L2正则化

先看一下知乎的一段解答来了解一下基本的知识

r(d)可以理解为有d的参数进行约束，或者 D 向量有d个维度。
咱们将楼主的给的凸优化结构细化一点，别搞得那么抽象，不好解释；

, 其中，
咱们可以令: f() = .

ok，这个先介绍到这里，至于f(x)为什么用多项式的方式去模拟？相信也是很多人的疑问，很简单，大家看看高等数学当中的泰勒展开式就行了，任何函数都可以用多项式的方式去趋近，log x,lnx,等等都可以去趋近，而不同的函数曲线其实就是这些基础函数的组合，理所当然也可以用多项式去趋近，好了，这个就先解释到这里了。

接下来咱们看一下拟合的基础概念。
首先，用一个例子来理解什么是过拟合，假设我们要根据特征分类{男人X，女人O}。
请看下面三幅图，x1、x2、x3；

这三幅图很容易理解：
1、 图x1明显分类的有点欠缺，有很多的“男人”被分类成了“女人”。
2、 图x2虽然有两个点分类错误，但是能够理解，毕竟现实世界有噪音干扰，比如有些人男人留长发、化妆、人妖等等。
3、 图x3分类全部是正确的，但是看着这副图片，明显觉得过了，连人妖都区分的出来，可想而知，学习的时候需要更多的参数项，甚至将生殖器官的形状、喉结的大小、有没有胡须特征等都作为特征取用了，总而言之f(x)多项式的N特别的大，因为需要提供的特征多，或者提供的测试用例中我们使用到的特征非常多(一般而言，机器学习的过程中，很多特征是可以被丢弃掉的)。

 

好了，总结一下三幅图：
x1我们称之为【欠拟合】
x2我们称之为【分类正拟合】，随便取的名字，反正就是容错情况下刚好的意思。
x3我们称之为【过拟合】，这种情况是我们不希望出现的状况，为什么呢？很简单，它的分类只是适合于自己这个测试用例，对需要分类的真实样本而言，实用性可想而知的低。

恩，知道了过拟合是怎么回事之后，我们来看一下如何去规避这种风险。先不管什么书上说的、老师讲的、经验之说之类的文言文。咱们就站在第一次去接触这种分类模型的角度去看待这个问题，发散一下思维，我们应该如何去防止过拟合？
显而易见，我们应该从【过拟合】出现的特征去判别，才能规避吧？
显而易见，我们应该、而且只能去看【过拟合】的f(x)形式吧？
显而易见，我们从【过拟合】的图形可以看出f(x)的涉及到的特征项一定很多吧，即等等很多吧？
显而易见，N很大的时候，是等数量增长的吧？
显而易见，w系数都是学习来的吧？

So，现在知道这些信息之后，如何去防止过拟合，我们首先想到的就是控制N的数量吧，即让N最小化吧，而让N最小化，其实就是让W向量中项的个数最小化吧？
其中，W=()

PS: 可能有人会问，为什么是考虑W，而不是考虑X?很简单，你不知道下一个样本想x输入的是什么，所以你怎么知道如何去考虑x呢？相对而言，在下一次输入,即第k个样本之前，我们已经根据次测试样本的输入，计算(学习)出了W.就是这么个道理，很简单。

我们再来思考，如何求解“让W向量中项的个数最小化”这个问题，学过数学的人是不是看到这个问题有点感觉？对，没错，这就是0范数的概念！什么是范数，我在这里只是给出个0-2范数定义，不做深究，以后有时间在给大家写点文章去分析范数的有趣玩法；
0范数，向量中非零元素的个数。
1范数，为绝对值之和。
2范数，就是通常意义上的模。

PS，貌似有人又会问，上面不是说求解“让W向量中项的个数最小化”吗？怎么与0范数的定义有点不一样，一句话，向量中0元素，对应的x样本中的项我们是不需要考虑的，可以砍掉。因为没有啥意义，说明项没有任何权重。so，一个意思啦。

 

r(d) = “让W向量中项的个数最小化” =

所以为了防止过拟合，咱们除了需要前面的相加项最小，即楼主公式当中的
=  （支出向量机的目标函数）最小，我们还需要让r(d)=最小，所以，为了同时满足两项都最小化，咱们可以求解让和r(d)之和最小，这样不就同时满足两者了吗？如果r(d) 过大，再小也没用；相反r(d)再小，太大也失去了问题的意义。
说到这里我觉得楼主的问题我已经回答了，那就是为什么需要有个r(d)项，为什么r(d)能够防止过拟合原因了。

 

书本中，或者很多机器学习的资料中，为了让全球的机器学习人员有个通用的术语，同时让大家便于死记硬本，给我上一段黑体字的部分的内容加上了一坨定义，例如：
我们管叫做经验风险，管上面我们思维导图的过程叫做正则化，所以顺其自然的管r(d)叫做正则化项，然后管+r(d) 叫做结构风险，所以顺其自然的正则化就是我们将结构风险最小化的过程，它们是等价的。
By the way，各位计算机界的叔叔、阿姨、伯伯、婶婶，经过不懈的努力，发现了这个公式很多有意思的地方，它们发现0范数比较恶心，很难求，求解的难度是个NP完全问题。然后很多脑袋瓜子聪明的叔叔、阿姨、伯伯、婶婶就想啊，0范数难求，咱们就求1范数呗，然后就研究出了下面的等式：

一定的条件我就不解释了，这里有一堆算法，例如主成分KPCA等等，例子我就不在举了，还是原话，以后我会尽量多写点这些算法生动点的推到过程，很简单，注重过程，不要死记硬背书本上的结果就好。
上面概括而言就是一句话总结：1范数和0范数可以实现稀疏，1因具有比L0更好的优化求解特性而被广泛应用。然后L2范数，是下面这么理解的，我就直接查别人给的解释好了，反正简单，就不自己动脑子解释了：
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的正则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦；所以大家比起1范数，更钟爱2范数。
所以我们就看到书籍中，一来就是，r(d)= 或者r(d)= 这种结构了，然后在机器学习当中还能看到下面的结构：
min{ } ，>=0
都是这么来的啦，万变不离其中。

 

 

接下来看另一段解答：

噪声，是指那些不能代表数据真实特性的数据点，它们的生成是随机的。学习和捕捉这些数据点让你的模型复杂度增大，有过拟合的风险。

避免过拟合的方式之一是使用交叉验证（cross validation），这有利于估计测试集中的错误，同时有利于确定对模型最有效的参数。本文将重点介绍一种方法，它有助于避免过拟合并提高模型的可解释性。

                                                             正则化

正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。

一个简单的线性回归关系如下式。其中 Y 代表学习关系，β 代表对不同变量或预测因子 X 的系数估计。

Y ≈ β0 + β1X1 + β2X2 + …+ βpXp

拟合过程涉及损失函数，称为残差平方和（RSS）。系数选择要使得它们能最小化损失函数。

  就是上面的预测Y

这个式子可以根据你的训练数据调整系数。但如果训练数据中存在噪声，则估计的系数就不能很好地泛化到未来数据中。这正是正则化要解决的问题，它能将学习后的参数估计朝零缩小调整。

 

岭回归

上图展示了岭回归（Ridge Regression）。这一方法通过添加收缩量调整残差平方和。现在，系数要朝最小化上述函数的方向进行调整和估计。其中，λ 是调整因子，它决定了我们要如何对模型的复杂度进行「惩罚」。模型复杂度是由系数的增大来表现的。我们如果想最小化上述函数，这些系数就应该变小。这也就是岭回归避免系数过大的方法。同时，注意我们缩小了每个变量和响应之间的估计关联，除了截距 β0 之外——这是因为，截距是当 xi1 = xi2 = …= xip = 0 时对平均值的度量。

当 λ=0 时，惩罚项没有作用，岭回归所产生的参数估计将与最小二乘法相同。但是当 λ→∞ 时，惩罚项的收缩作用就增大了，导致岭回归下的系数估计会接近于零。可以看出，选择一个恰当的 λ 值至关重要。为此，交叉验证派上用场了。由这种方法产生的系数估计也被称为 L2 范数（L2 norm）。

标准的最小二乘法产生的系数是随尺度等变的（scale equivariant）。即，如果我们将每个输入乘以 c，那么相应的系数需要乘以因子 1/c。因此，无论预测因子如何缩放，预测因子和系数的乘积（X{β}）保持不变。但是，岭回归当中却不是如此。因此，我们需要在使用岭回归之前，对预测因子进行标准化，即将预测因子转换到相同的尺度。用到的公式如下：

Lasso 回归

Lasso 是另一个变体，其中需要最小化上述函数。很明显，这种变体只有在惩罚高系数时才有别于岭回归。它使用 |β_j|（模数）代替 β 的平方作为惩罚项。在统计学中，这被称为 L1 范数。

让我们换个角度看看上述方法。岭回归可以被认为是求解一个方程，其中系数的平方和小于等于 s。而 Lasso 可以看作系数的模数之和小于等于 s 的方程。其中，s 是一个随收缩因子 λ 变化的常数。这些方程也被称为约束函数。

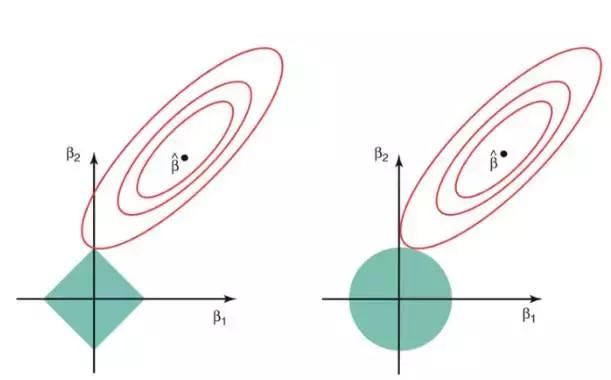
假定在给定的问题中有 2 个参数。那么根据上述公式，岭回归的表达式为 β1² + β2² ≤ s。这意味着，在由 β1² + β2² ≤ s 给出的圆的所有点当中，岭回归系数有着最小的 RSS（损失函数）。

同样地，对 Lasso 而言，方程变为 |β1|+|β2|≤ s。这意味着在由 |β1|+|β2|≤ s 给出的菱形当中，Lasso 系数有着最小的 RSS（损失函数）。

下图描述了这些方程。

上图的绿色区域代表约束函数域：左侧代表 Lasso，右侧代表岭回归。其中红色椭圆是 RSS 的等值线，即椭圆上的点有着相同的 RSS 值。对于一个非常大的 s 值，绿色区域将会包含椭圆的中心，使得两种回归方法的系数估计等于最小二乘估计。但是，上图的结果并不是这样。在上图中，Lasso 和岭回归系数估计是由椭圆和约束函数域的第一个交点给出的。因为岭回归的约束函数域没有尖角，所以这个交点一般不会产生在一个坐标轴上，也就是说岭回归的系数估计全都是非零的。然而，Lasso 约束函数域在每个轴上都有尖角，因此椭圆经常和约束函数域相交。发生这种情况时，其中一个系数就会等于 0。在高维度时（参数远大于 2），许多系数估计值可能同时为 0。

这说明了岭回归的一个明显缺点：模型的可解释性。它将把不重要的预测因子的系数缩小到趋近于 0，但永不达到 0。也就是说，最终的模型会包含所有的预测因子。但是，在 Lasso 中，如果将调整因子 λ 调整得足够大，L1 范数惩罚可以迫使一些系数估计值完全等于 0。因此，Lasso 可以进行变量选择，产生稀疏模型。

 

正则化有何效果？

标准的最小二乘模型常常产生方差。即对于与训练集不同的数据集，模型可能不能很好地泛化。正则化能在不显著增大偏差的的同时，显著减小模型的方差。因此，正则化技术中使用的调整因子 λ，能控制对方差和偏差的影响。当 λ 的值开始上升时，它减小了系数的值，从而降低了方差。直到上升到某个值之前，λ 的增大很有利，因为它只是减少方差（避免过拟合），而不会丢失数据的任何重要特性。但是在某个特定值之后，模型就会失去重要的性质，导致偏差上升产生欠拟合。因此，要仔细选择 λ 的值。

这就是你开始使用正则化之前所要掌握的全部基础，正则化技术能够帮助你提高回归模型的准确性。实现这些算法的一个很流行的库是 Scikit-Learn，它可以仅仅用 Python 中的几行代码运行你的模型。

 

正则化项即罚函数，该项对模型向量进行“惩罚”，从而避免单纯最小二乘问题的过拟合问题。正则化项本质上是一种先验信息，整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计的形式，如果你将这个贝叶斯最大后验估计的形式取对数，即进行极大似然估计，你就会发现问题立马变成了损失函数+正则化项的最优化问题形式。
好，接下来我来举个例子，就拿Lasso来说吧：Lasso中中的目标函数即相当于如下的后验概率：

其中

(47)是似然函数，对应于Lasso中的损失函数，(48)是先验概率，相当于Lasso中的正则化项。可以看出，Lasso的正则化项从贝叶斯观点来看就是以Laplace先验信息。
采用不同的先验信息，可得到不同的结果。因此，你可以设计其它的先验信息构成新的正则化项。