Suphx:微软麻将AI算法以及Q&A摘要
注:微软研究院的Suphx团队已经对论文进行了详细的解读,这里只是我自己读原论文算法部分的记录,以及对Suphx团队在4月9日的直播中的Q&A部分的摘要。
Suphx(Super Phoenix)是一个主攻4人日本麻将的AI,主要基于深度强化学习进行训练,除此之外还应用了全局奖励预测(global reward predictction)、先知教练(oracle guiding)以及运行时策略适应(run-time policy adaption)等新技术,在最大的日本麻将在线对战平台天凤(tenhou.net)上超过了99%的人类玩家。
目录
- 麻将的困难之处
- Suphx的决策流程
- 模型结构
- 算法
- 全局奖励预测(Global Reward Predictction)
- 先知教练(Oracle Guiding)
- 参数化蒙特卡洛策略适应(Parametric Monte-Carlo Policy Adaption)
- Q&A摘录
- Reference
麻将的困难之处
麻将是一个不完全信息多人游戏,它的复杂规则、计分方式和隐藏信息使它变成一个充满挑战的AI研究项目:
- 游戏规则:麻将有许多种动作(actions),包括立直、吃、碰、杠、舍牌等,而且这些动作之间的顺序会被鸣牌、抢杠等打断。因此构建一个游戏树非常复杂,而且就算构造出来,在同一个选手的两个连续动作之间会包含大量的路径,因此在过往类似项目中效果很好的蒙特卡洛树搜索(Monte-Carlo tree search,MCTS)以及Counterfactual Regret(CFR)最小化都很难直接应用在麻将中。
- 计分方式:一次麻将对战由许多局组成,比如日麻中最常见的半庄战通常由8-12局组成,最终排名由选手的累计分数决定,因此每局游戏的得失分数并不能反映选手打的好坏。比如最后一局中,分数最高的选手在领先优势较大的情况下可以选择给分数低的选手放铳来确保以一位结束比赛。另外麻将中和牌的大小跟概率通常负相关,因此分数和速度的取舍也是反应选手实力的重要部分。
- 隐藏信息:在麻将中每个选手有最多13张牌是别的选手看不到的,除此之外牌山中还有14张牌是摸不到的,摸得到的70张牌也只会在被人摸到并打出之后才可见。因此在每个决策点有 1 0 48 10^{48} 1048种隐藏状态需要考虑,比之前研究过的不完全信息游戏(比如德州扑克)要多许多,因此AI也更难把奖励跟观察到的信息联系起来。
Suphx的决策流程
为了解决这些问题,Suphx使用了5个深度卷积神经网络:舍牌模型(Discard model)、立直模型(Riichi model)、吃模型(Chow model)、碰模型(Pong model)和杠模型(Kong model),每个模型的功能如下表所示:
| 模型 | 功能 |
|---|---|
| 舍牌模型 | 在通常情况下决定要舍哪张牌 |
| 立直模型 | 决定是否立直 |
| 吃模型 | 决定是否吃以及怎么吃 |
| 碰模型 | 决定是否碰 |
| 杠模型 | 决定是否杠 |
这些网络先用专业选手的牌谱进行训练,然后被用在深度强化学习中作为策略进行自我对局(self-play)。除此之外还有一个基于规则的模型来决定是否和牌。完整的决策流程见下图:
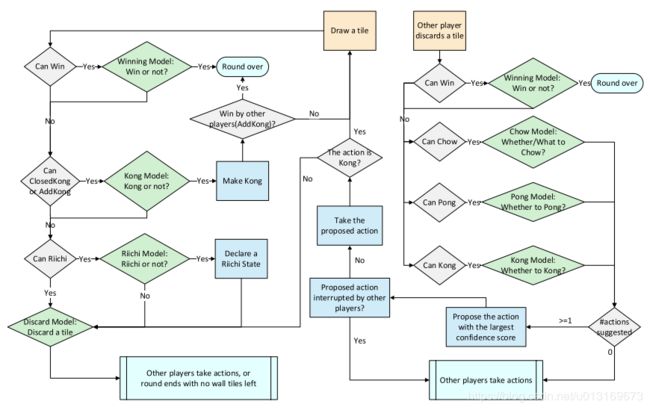
模型结构
日本麻将中总共有34张不同的牌,所以Suphx中使用多个 34 × 1 34 \times 1 34×1的通道来表示场上的状态,比如手牌可以用四个通道来编码,如下图所示:
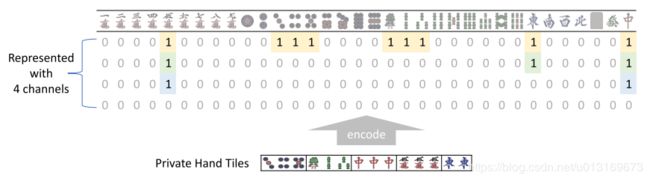
类似的,副露、宝牌以及舍牌顺序也通过这种方式进行编码。分类特征(categorical feature)用全为 0 0 0或 1 1 1的多个通道来编码。整数特征(integer feature)则会被区间化,然后每个区间用全为 0 0 0或 1 1 1的通道来编码。
除了这些直接可见的状态之外,作者还设计了look-ahead特征用来表示打出某一张牌后赢牌向听数和分数,例如使用一个特征来表示打出某张牌后能否在进3张牌后和出12000点。由于日麻中总共有89种面子和34种对子,能和的牌型数量非常多,所以作者没有考虑对手的行为(例如通过舍牌判断是否在做混一色/清一色),只是用深度优先搜索来计算自己和出各种牌型的概率。在这种简化之下,总共构建出100多种look-ahead特征,每种特征都用一个34维的向量来表示。
除了输入和输出维度之外,所有模型的网络结构都差不多,具体结构和维度如下图下表所示。在吃、碰、杠模型中,除了状态特征和look-ahead特征以外,还有对哪些牌吃、碰、杠的信息。另外,这些模型都是没有池化层的,因为每个通道中的每一列都有自己的含义,所以池化之后会导致信息损失。
各模型输入输出维度:
| 模型 | 输入维度 | 输出维度 |
|---|---|---|
| 舍牌模型 | 34 × 838 34 \times 838 34×838 | 34 34 34 |
| 立直模型 | 34 × 838 34 \times 838 34×838 | 2 2 2 |
| 吃模型 | 34 × 958 34 \times 958 34×958 | 2 2 2 |
| 碰模型 | 34 × 958 34 \times 958 34×958 | 2 2 2 |
| 杠模型 | 34 × 958 34 \times 958 34×958 | 2 2 2 |
算法
Suphx的学习过程分为三个阶段:
- 通过监督学习训练5个模型。训练用的 (state, action) 对来自天凤平台上的顶尖人类选手。
- 用训练过的模型作为策略来进行self-play,并通过熵正则化分布式强化学习(Distributed Reinforcement Learning with Entropy Regularization)来更新策略。在训练过程中使用了全局奖励预测(global reward predictction)和先知教练(oracle guiding)来处理麻将中特有的困难之处。
- 在online playing过程中使用了运行时策略适应(run-time policy adaption)来针对本局游戏的初始状态进行调整以获得更好的表现。
下面详细介绍Suphx中提出的几个算法。
全局奖励预测(Global Reward Predictction)
在麻将中,每一场游戏通常由许多局组成,比如天凤中的一场游戏包含8-12局。在每一局游戏的结束后,和牌的选手会获得正分,其他选手则为0分或负分,而在每一场游戏的最后,选手在这场游戏中的每一局的得分会被加起来得到最终得分,并以此计算排名。然而以每一局的得分或者游戏的最终得分来作为强化学习的训练信号都不太合适,因为:
- 如果用一场游戏的最终得分来训练,则每一局都会有一样的训练信号,那么就无法区分打得好跟打得不好的对局;
- 如果用每一局的得分来训练,则不一定能真实反映选手水平。比如在一场游戏的最后几局,有很大优势的一位选手会打得比较保守,可能会让三位或四位的选手的获得胜利来确保自己可以在这一场游戏结束时处于第一位。那么这几局里面的获得的负的分数并不能说明该选手的策略不好,相反这是一个好策略的体现。
因此为了给强化学习的训练提供一个更有效的训练信号,需要在每一局去估算这场游戏的最终得分。作者提出了一个全局奖励预测器 Φ \Phi Φ来通过这一局以及本场游戏之前所有局的信息来预测最终得分,以此作为强化学习训练信号。在Suphx中, Φ \Phi Φ是一个两层的门控循环单元( G R U \mathtt{GRU} GRU)接两层全连接层构成的循环神经网络,如下图所示:
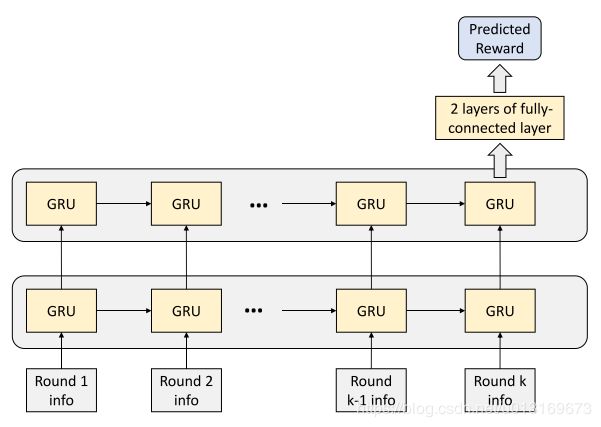
Φ \Phi Φ的训练数据来自天凤顶尖选手的对局记录,它的训练目标是最小化如下所示的均方误差:
min 1 N ∑ i = 1 N 1 K i ∑ j = 1 K i ( Φ ( x i 1 , x i 2 , ⋯ , x i j ) − R i ) 2 , \min\frac{1}{N}\sum^{N}_{i=1}\frac{1}{K_i}\sum^{K_i}_{j=1}\left(\Phi(x^1_i, x^2_i, \cdots, x^j_i)-R_i\right)^2, minN1i=1∑NKi1j=1∑Ki(Φ(xi1,xi2,⋯,xij)−Ri)2,
其中 N N N是训练数据中的游戏场数, R i R_i Ri是第 i i i场游戏的最终得分, K i K_i Ki是第 i i i场游戏的局数, x i k x_i^k xik是第 i i i场游戏的第 k k k局的特征,包括这一局的分数、此时的累积分数、庄家的位置、本场棒和立直棒。
当 Φ \Phi Φ训练好后,对于有 K K K局的self-play,第 k k k局就会用 Φ ( x k ) − Φ ( x k − 1 ) \Phi(x^k)-\Phi(x^{k-1}) Φ(xk)−Φ(xk−1)作为强化学习训练的奖励。
先知教练(Oracle Guiding)
在麻将中有非常多的隐藏信息,在这种情况下用强化学习来学习策略会非常慢。为了加速训练,作者使用了一个可以获取完全信息的先知智能体(oracle agent)。完全信息包括:
- 当前选手的手牌
- 所有选手的副露及弃牌
- 其他公开的信息比如累积分数、立直棒等
- 另外三名选手的手牌
- 牌山上的牌
对于一个通常智能体(normal agent,指没有完全信息的agent)来说,只有前三项是可见的。
由于拥有完全信息,oracle agent可以通过强化学习很快精通麻将,问题是怎么让oracle agent来加速normal agent的训练。在这里普通的知识蒸馏(knowledge distillation)的效果并不好,因为一个没有完全信息的normal agent很难去模仿oracle agent的行为。在Suphx中采用的方式是先用完全信息进行训练oracle agent,然后通过drop out的方式逐渐减少完全信息中的特征,慢慢地让oracle agent转变为normal agent。在oracle agent完全转变为normal agent后,还会进行一定轮次的训练。此时学习率会降到之前的 1 / 10 1/10 1/10,并且会拒绝重要性大于某个阈值的state-action对。如果不添加这两个限制,后续的训练就会不稳定,性能也不会获得提升。
参数化蒙特卡洛策略适应(Parametric Monte-Carlo Policy Adaption)
在麻将中,人类会在拿到不同的手牌的时候使用不同的策略,比如会在拿到好的起手的时候打得更激进来赢得更多分数,在拿到不太好的起手的时候打得保守一点来避免更大的损失。所以如果可以把离线训练的策略针对起手做一定的适应,那么就很可能可以获得更好的表现。跟围棋或星际争霸不同,蒙特卡洛树搜索(Monte-Carlo tree search,MCTS)在麻将上的表现并不好,因此作者提出了一种新的方法,名为参数化蒙特卡洛策略适应(parametric Monte-Carlo policy adaption,pMCPA)。
当一局麻将开始,agent摸了初始手牌之后,对离线训练的策略按以下方式进行调整:
- 模拟:固定自己的手牌,对另外三个选手的手牌及牌山的牌进行随机采样,然后用离线训练的策略来试运行游戏并记录出牌顺序。总共记录 K K K个出牌顺序。
- 适应:根据这 K K K个出牌顺序用策略梯度来微调离线训练的策略。
- 推理:用微调过的策略来进行本局游戏。
根据作者的研究, K K K不需要非常大, p M C P A \mathtt{pMCPA} pMCPA也不需要记录本局游戏的统计信息。因为 p M C P A \mathtt{pMCPA} pMCPA是参数化的方法,所以通过 K K K次模拟更新过的策略可以对未见过的状态进行估计,也就是说这种在线适应方法对模型在有限次模拟中学到的知识的泛化有帮助。
详细的训练过程、损失函数定义以及实验结果请参考原论文。
Q&A摘录
作者团队在4月9日的直播(https://www.bilibili.com/video/BV11z411b7jk )中对论文的技术细节进行了补充,下面是Q&A部分的摘要:
- 自适应算法在天凤对局中应用:因为天凤上的时间限制,自适应算法没有应用到天凤平台上的对局中。
- 用的显卡数量:训练时用了几十张基础显卡,论文中有详细说明。数量不多,可以考虑自行复现。
- 赤宝牌:有考虑赤宝牌,具体是用3个通道来表示三种赤宝牌。
- 为什么ResNet要用50层:是一个折中的选择,如果使用更多的层数,accuracy会有提高,但是也需要更多的算力;如果使用更少的层数,则可能会无法看到所有通道,会对性能造成影响。
- Suphx找到的是不是近似的纳什均衡:不能保证。第一是多人博弈很难找到纳什均衡,第二是就算找到了,由于是多人博弈,它的效果也不一定很好。
- 为什么用CNN:因为CNN可以学习复杂的手牌形状,比如混一色、三色同顺等。
- Policy Adaptation会不会过拟合:不会,因为在每一局开始policy都会重置为离线训练好的最佳policy。
- 从零开始RL会怎么样:会花比较长时间,但是最后胡牌率跟放铳率会变得跟正常人类玩家一样。
- 有没有训练过value function:在麻将中训练value function很难,比如就算听牌了,也不知道点炮跟和牌哪个来得更快。
- 对手的性格及牌风差异会不会影响策略:没有显式对对手进行建模,只是通过学习高手对局来隐式学习应对方法。
- 有没有用过transformer:正在尝试,但是前期还是从CNN开始。
- 有没有试着把CNN整合在一起:整合在一起从研究上来讲会更漂亮,但是需要对可能会引入的额外dependency进行trade-off,以及时间和资源的限制,所以暂时没有做。
- 有上线计划吗:正在跟天凤那边沟通,之后也会考虑提供一个service来供大家使用。
- 有没有用时间信息,比如别家思考时间等:没有使用。
- look-ahead feature:论文里面已经说的很详细了,这里面比较有趣的一个点就是其实和牌概率是可以显式算出来的,通过判断需要什么牌,场上还有多少张,是可以算出胡牌概率的。
- 训练RL的时候为什么只更新弃牌模型:更新别的模型也能提高性能,但是提高得没有弃牌模型那么多,所以为了跑更多iteration就只更新弃牌模型了。
- Reward Predictor是否用self-play进行训练:没有,只使用了人类的数据训练。
- Oracle guiding的mask理论上能不能保证收敛性:暂时没有进行证明,而且deep RL的理论很多都是不太清楚的。
- 打牌时的机器配置:50层的ResNet算力需求不高,比较强一点的CPU机器问题都不大。
- 模型输入:是通过模拟器导出的设计好的特征,不是图片。
Reference
Li, Junjie, et al. “Suphx: Mastering Mahjong with Deep Reinforcement Learning.” ArXiv Preprint ArXiv:2003.13590, 2020. https://arxiv.org/abs/2003.13590
微软中国视频中心, “4月9日直播丨揭秘微软超级麻将AI Suphx背后的技术!”, 2020. https://www.bilibili.com/video/BV11z411b7jk

