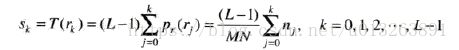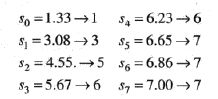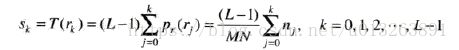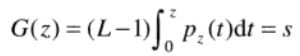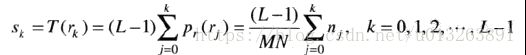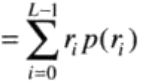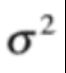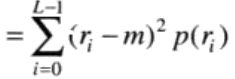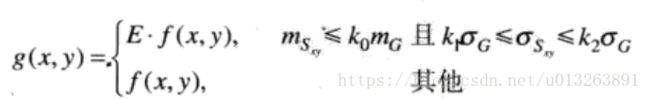直方图均衡化、规定化、局部直方图、直方图统计
一、直方图均衡
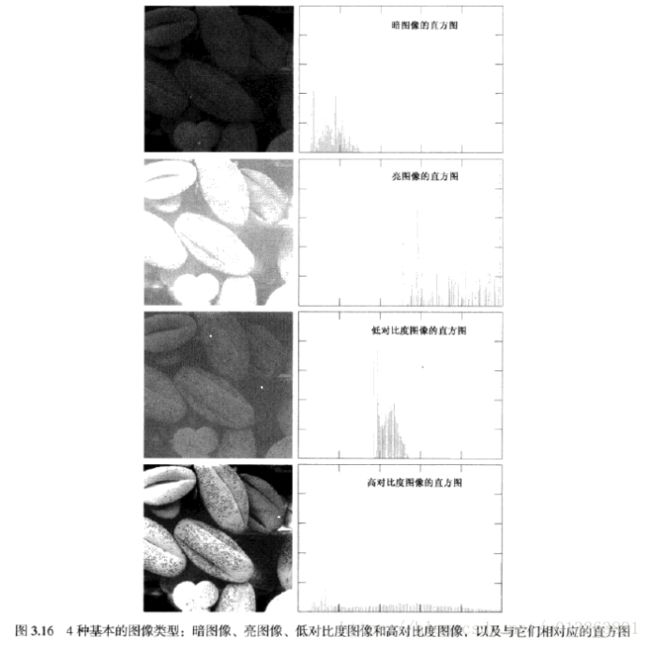
如图3.16所示,是4个基本灰度级为特征的花粉图像:暗图像、亮图像、低对比度图像和高对比度图像,右侧显示了与这些图像对应的直方图。
由四张图的对比我们可知,如一幅图像的像素倾向于占据整个可能的灰度级并分布均匀,则该图像会有高对比度的外观并展示灰色调的变换,最终效果将会是一幅灰度细节丰富且动态范围较大的图像。图像均衡化即是实现这种效果。2 直方图均衡化推导过程
1.1 连续灰度值的直方图均衡化推导过程
连续灰度值的情况下,一幅图像的灰度级可以看成【0,L-1】内的随机变量。随机变量的基本描绘子是其概率密度函数(PDF)。r表示输入图像的灰度值,s表示均衡化之后的图像的灰度值,pr(r)和ps(s)表示随机变量r和s的PDF,因为r为输入图像的像素,所有pr(r)可以求得,则变换之后的s的PDF:
令
由上式可以看出s的PDF始终是均匀的。
1.2 离散灰度值的直方图均衡化推导过程
对于离散值的灰度值,我们处理其概率与求和来代替PDF和积分。一幅图像中rk出现的概率近似为:
M表示行 N表示列 MN表示图像中像素的总数,nk表示灰度为rk的个数
1.3 直方图均衡使用举例
其他与s0,s1求法相同,把他们近似为最接近的整数。
这些是均衡化之后的直方图的值,r0映射为1,r1映射为3,r2映射为5,r3映射为6,r4映射为6,r5,r6,r7映射为7,根据r中对应的像素个数,
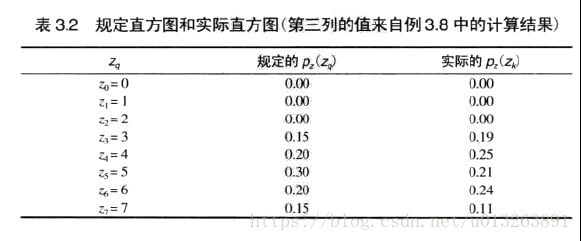
1对应的像素个数为790,概率为0.19,
3对应的像素个数为1023,对应的概率为0.25,
5对应的像素个数为850,对应的概率为0.21,
6对应的像素个数为985,对应的概率为0.24,
7对应的像素个数为448,对应的概率为0.11
下面第一张是原始的图像的直方图,第二张是均衡化之后的直方图
1.4 C++实现
- 求输入图像中每一个灰度级别的元素个数
- 根据每一个灰度级别的个数求该灰度级别所占的概率
- 根据下式求新的灰度级别
4.找到r和s的对应关系
5.根据对应关系为图像赋新的灰度值
#include
#include
int main() {
cv::Mat src=cv::imread("../1.jpg",0);
int gray[256]={0};//记录灰度级别下的像素个数
int mn=src.cols*src.rows;//像素总数
double r_prob[256]={0};//输入图像的概率
double pdf[256]={0};//累积概率密度
double r[256]={0};//r与s的映射
double s_prob[256]={0};//均衡化之后的概率
//统计每个灰度级别下的像素个数
cv::Mat dst=src.clone();
for(int row=0;row(row,col);
gray[g]++;
}
}
//计算每一个像素级别的概率
for(int i=0;i<256;i++){
r_prob[i]=((double)gray[i])/mn;
}
pdf[0]=r_prob[0];
for(int i=1;i<256;i++){
pdf[i]=pdf[i-1]+r_prob[i];
}
//每个输入的灰度级别对应的输出的灰度级别
for(int i=0;i<256;i++)
{
int c=cvRound(255*(pdf[i]));
r[i]=c;
}
for(int row=0;row(row,col);
dst.at(row,col)=r[g];//重新赋值新的灰度级别
}
}
cv::imshow("src",src);
cv::imshow("dst",dst);
int bins=256;
int hist_size[]={bins};
float range[]={0,256};
const float* ranges[]={range};
cv::Mat histsrc,histdst;
int channels[]={0};
cv::calcHist(&src,1,channels,cv::Mat(),histsrc,1,hist_size,ranges,true,false);
cv::calcHist(&dst,1,channels,cv::Mat(),histdst,1,hist_size,ranges);
std::cout<(0.9*256);
for(int i=0;i<256;i++){
float binValue=histsrc.at(i);
int realValue=cv::saturate_cast(binValue*hpt/maxValue);
cv::rectangle(srcImage,cv::Point(i*scale,255),cv::Point((i+1)*scale-1,256-realValue),
cv::Scalar(255));
}
cv::minMaxLoc(histdst,&minValue,&maxValue,0,0);
hpt=cv::saturate_cast(0.9*256);
for(int i=0;i<256;i++){
float binValue=histdst.at(i);
int realValue=cv::saturate_cast(binValue*hpt/maxValue);
cv::rectangle(dstImage,cv::Point(i*scale,255),cv::Point((i+1)*scale-1,256-realValue),
cv::Scalar(255));
}
cv::imshow("srcImage",srcImage);
cv::imshow("dstImage",dstImage);
cv::waitKey(0);
return 0;
} 1.5 直方图均衡化处理结果
上图左侧为原始图像,右侧为均衡化之后的结果,可以看出均衡化之后的图像对比度有明显的增强
二、 直方图规定化
用于产生处理之后有特殊的直方图的方法称为直方图匹配或直方图规定化。
2.1 连续直方图规定化的推导
假设连续灰度r和z分别表示输入图像和输出图像的灰度级,r和z看成连续随机分量,pr(r),pz(z)是我们希望输出图像所具有的指定概率密度函数。
令s:
随机变量z:
G(z)=T(r),因此
步骤:
- 由输入的图像得到pr(r),并可以由下式得到s的值
- 使用下式中指定的PDF求得变换函数G(z)
- 求得反变换函数z=G-1(s),因为z是由s得到的,所以该处理是s到z的映射,z是我们期望得到的值
2.2 连续灰度值直方图规定化的一个简单例子
由上面的例子我们可以得到结论,在连续灰度值时,pr(r)已知,如果我们想得到一个概率分布函数是pz(z)的图像,只需
即可得到r与z之间的映射关系
2.3 离散直方图均衡化的推导过程
![]()
得到q与k的对应关系
步骤:
- 计算给定的直方图的pr(r),使用它得到sk四舍五入到【0,L-1】的整数
- 对q=0,1,2,3...计算变换函数G的所有值,其中pz(zi)是规定的直方图的值,同样四舍五入为范围【0,L-1】内的整数,并将G存在一个表中
- 对于每一个值sk,使用G值寻找对应的zq,使得G(zq)最接近sk,并存储s到z的映射,当满足sk的zq多于一个时,选择最小的值
2.4 离散直方图均衡化的例子
希望将表3.1灰度灰度直方图值转换为表3.2第二列的灰度直方图值
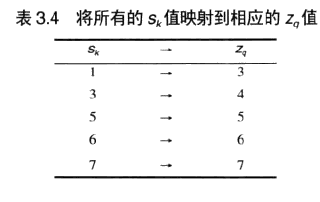
最终得到表3.4的映射表
z3对应的G(z3)=1,也就是sk=1,对应的是r0
z4对应的是G(z4)=3,sk=3,对应的是r1
z5对应的是G(z5)=5,sk=5,对应的是r2
z6对应的是G(z6)=6,sk=6,对应的是r3,r4
z7对应的是G(z7)=7,sk=7,对应的是r5,r6,r7
最后得到的图像是将输入图像为0的输出图像的灰度值变为3
输入图像为灰度值为1的变为输出图像灰度值为4
输入图像为灰度值为2的变为输出图像灰度值为5
输入图像为灰度值为3,4的变为输出图像灰度值为6
输入图像为灰度值为5,6,7的变为输出图像灰度值为7
2.5 C++实现
#include
#include
#define K1 0.002
#define A1 1
#define A2 0.07
#define U1 0.15
#define SIG1 0.05
#define U2 0.75
#define SIG2 0.05
#define pi 3.1415626535627
inline double twoModeGauss(double r){
double w=K1+(A1/sqrt(2*pi)*SIG1)*exp(-(pow((r-U1),2.0)
/(2*pow(SIG1,2.0))))+(A2/sqrt(2*pi)*SIG2)*exp(-(pow((r-U2),2.0)/(2*pow(SIG2,2.0))));
return w;
}
cv::Mat showHist(cv::Mat src)
{
int bins=256;
int hist_size[]={bins};
float range[]={0,256};
const float* ranges[]={range};
cv::Mat histsrc;
int channels[]={0};
cv::calcHist(&src,1,channels,cv::Mat(),histsrc,1,hist_size,ranges,true,false);
int scale=1;
cv::Mat srcImage(256*scale,256,CV_8U,cv::Scalar(0));
double maxValue=0;
double minValue=0;
cv::minMaxLoc(histsrc,&minValue,&maxValue,0,0);
int hpt=cv::saturate_cast(0.9*256);
for(int i=0;i<256;i++){
float binValue=histsrc.at(i);
int realValue=cv::saturate_cast(binValue*hpt/maxValue);
cv::rectangle(srcImage,cv::Point(i*scale,255),cv::Point((i+1)*scale-1,256-realValue),
cv::Scalar(255));
}
cv::imshow("src",srcImage);
}
int main() {
cv::Mat src=cv::imread("../2.png",0);
int gray[256]={0};//记录灰度级别下的像素个数
int mn=src.cols*src.rows;//像素总数
double r_pdf[256]={0};//输入图像的概率
double r_cdf[256]={0};//累积概率密度
double r[256]={0};//对应的s T(r)
int z[256]={0};//对应的G(z)
double z_pdf[256];//pz(z)
double z_cdf[256]={0};//z的累积分布概率
cv::Mat dst=src.clone();
cv::Mat spe=src.clone();
//记录灰度级别下的像素个数
for(int row=0;row(row,col);
gray[g]++;
}
}
z_pdf[0]=0;
double sum=0;
for(int i=0;i<256;i++){
double r=(double)i/256.0;
z_pdf[i+1]=twoModeGauss(r);
sum+=z_pdf[i+1];
}
//计算pr(r)和pz(z)
for(int i=0;i<256;i++){
r_pdf[i]=((double)gray[i])/mn;
z_pdf[i]=z_pdf[i]/sum;
}
//计算r和z的cdf
z_cdf[0]=z_pdf[0];
r_cdf[0]=r_pdf[0];
for(int i=1;i<256;i++){
r_cdf[i]=r_cdf[i-1]+r_pdf[i];
z_cdf[i]=z_cdf[i-1]+z_pdf[i];
}
//每个输入的灰度级别对应的输出的灰度级别
for(int i=0;i<256;i++)
{
int c=cvRound(255*(r_cdf[i]));
int d=cvRound(255*(z_cdf[i]));
z[i]=d;
r[i]=c;
}
//均衡化
for(int row=0;row(row,col);
dst.at(row,col)=r[g];//重新赋值新的灰度级别
}
}
//规定化
for(int row=0;row(row,col);
for(int i=0;i<256;i++)
{
if(r[g]==z[i])
spe.at(row,col)=i;//此处是为了满足当多个z满足s时按照惯例选择小的那个
}
}
}
//显示图片
cv::imshow("src",src);
cv::imshow("dst",dst);
cv::imshow("spe",spe);
//显示直方图
showHist(src);
showHist(dst);
showHist(spe);
cv::waitKey(0);
return 0;
} 三、局部直方图处理
前面讨论的均为对整张图像进行的直方图处理,直方图处理对于局部同样适用。直方图处理技术可以用于局部增强。过程是定义一个邻域,并把该区域的中心从一个像素移至另一个像素。在每个位置,计算领域中点的直方图,并且得到的不是直方图的均衡化就是规定化的变换函数,这个函数最终用于映射邻域中心像素的灰度。然后,领域的中心被移至一个相邻像素位置,重复该过程。当邻域进行逐像素平移时,由于只有邻域中的一行或一列改变,所以可以在移动一步中,以新数据更新前一个位置得到的直方图。
步骤:
1)求第一个邻域内的直方图
2)根据直方图均衡化将该邻域中心点的像素更新
3)将中心点移向下一个邻域,比如,此时中心点为(3,3)(第一个数为行,第二个值为列)先向下移动一个像素,中心点变为(4,3),假设Size=7,则此时得到的邻域与前一个邻域相比只有一行像素不同,即(0,0)(0,1)..(0,6),与(7,0)(7,1)..(7,6)可能不同,此时比较第0行和第7行相对应的元素是否相同来更新直方图,如果直方图有变化,则更新当前中心点的像素值
4)对所有的像素点执行第三歩
#include
#include
void getCDF(float *s,const float *const c){
for(size_t i = 1;i<256;i++){
s[i] = s[i-1]+c[i];
}
}
int dim=3;
inline void refresh(float *c,int sub,bool flag){
if(flag){
c[sub]+=1.0/(dim*dim);
}
else
{
c[sub]-=1.0/(dim*dim);
}
}
void localhist(cv::Mat &img) {
int width = img.cols;
int height = img.rows;
float count[256];
for (size_t t = 0; t < 256; t++) {
count[t] = 0;
}
int sub = 0;
//第一次得到的统计直方图
for (int m = 0; m < dim; m++) {
for (int n = 0; n < dim; n++) {
sub = img.at(m, n);
count[sub] += (1.0 / (dim*dim));
}
}
float s[256]={0};
s[0] = count[0];
getCDF(s, count);
sub = img.at(dim/2, dim/2);
int newvalue = (int) ((s[sub]) * 255 + 0.5);
img.at(dim/2, dim/2) = newvalue;
refresh(count, sub, false);
refresh(count, newvalue, true);
for (int i = dim/2; i < width - (dim/2-1);) {
if (i % 2 == 1) {
for (int j = dim/2+1; j < height - (dim/2-1); j++) {
bool dirty = true;
for (int p = 0; p < dim; p++) {
int old = img.at(j - (dim/2+1), i - dim/2 + p);
int add = img.at(j + dim/2, i - dim/2 + p);
if (old != add) {
refresh(count, old, false);
refresh(count, add, true);
dirty = false;
}
}
if (!dirty) {
getCDF(s, count);
sub = img.at(j, i);
refresh(count, sub, false);
img.at(j, i) = (int) (s[sub] * 255 + 0.5);
refresh(count, img.at(j, i), true);
}
if (j + dim/2 == width - 1) {
i = i + 1;
for (int p = 0; p < dim; p++) {
int old = img.at(j - dim/2 + p, i - (dim/2+1));
int add = img.at(j - dim/2 + p, i + dim/2);
if (old != add) {
refresh(count, old, false);
refresh(count, add, true);
dirty = false;
}
}
if (!dirty) {
getCDF(s, count);
sub = img.at(j, i);
refresh(count, sub, false);
img.at(j, i) = (int) (s[sub] * 255);
refresh(count, img.at(j, i), true);
}
}
}
} else {
for (int j = height -(dim/2+1); j > dim/2-1; j--) {
bool dirty = true;
for (int p = 0; p < dim; p++) {
int old = img.at(j - dim/2, i - dim/2 + p);
int add = img.at(j + (dim/2+1), i - dim/2 + p);
if (old != add) {
refresh(count, old, false);
refresh(count, add, true);
dirty = false;
}
}
if (!dirty) {
getCDF(s, count);
sub = img.at(j, i);
refresh(count, sub, false);
img.at(j, i) = (int) (s[sub] * 255);
refresh(count, img.at(j, i), true);
}
if (j - dim/2 == 0) {
i = i + 1;
if(i==width-(dim/2-1))break;
for (int p = 0; p < dim; p++) {
int old = img.at(j - dim/2 + p, i - (dim/2+1));
int add = img.at(j - dim/2 + p, i + dim/2);
if (old != add) {
refresh(count, old, false);
refresh(count, add, true);
dirty = false;
}
}
if (!dirty) {
getCDF(s, count);
sub = img.at(j, i);
refresh(count, sub, false);
img.at(j, i) = (int) (s[sub] * 255);
refresh(count, img.at(j, i), true);
}
}
}
}
}
}
int main(){
cv::Mat src=cv::imread("../1.png",0);
cv::Mat img=src.clone();
localhist(img);
cv::imshow("src",src);
cv::imshow("dst",img);
cv::imwrite("../3.png",img);
cv::waitKey(0);
return 0;
} 实现的效果并不好
4 在图像增强中使用直方图统计
4.1 图像增强中使用直方图统计步骤
使用直方图统计实现图像中的暗区域图像增强的具体步骤:
1根据下式取得输入图像的平均灰度
2根据下式取得输入图像的方差
3判断一个区域在点(x,y)的局部平均灰度mSxy,局部标准差为我们取k0,k1,k2,E
当
时,我们把当前点看做较暗的点,此时我们将该像素点乘以E达到增大其灰度值
对于亮区域暗化与此相反。
4.2 C++实现
#include
#include
double getMean(double*r_pdf){
double m=0;
for(int i=0;i<256;i++)
m+=i*r_pdf[i];
return m;
}
double getVariance(double *r_pdf,double m)
{
double delta=0;
for(int i=0;i<256;i++)
if(r_pdf[i]!=0)
delta+=(pow((i-m),2)*r_pdf[i]);
return delta;
}
void init(double *r_pdf){
for(int i=0;i<256;i++){
r_pdf[i]=0;
}
}
int histStatistic(cv::Mat &src,int dim,float k0,float k1,float k2,float E){
if(dim%2==0){
return -1;
}
int width=src.rows;
int height=src.cols;
int mn=width*height;
double r_pdf[256]={};
for(int row=0;row(row,col);
r_pdf[g]+=1.0/mn;
}
}
double mean=getMean(r_pdf);
double delta=getVariance(r_pdf,mean);
double delta1=std::sqrt(delta);
double mxy=0;
double deltaxy=0;
double local=dim*dim;
for(int i=dim/2;i(p,q);
r_pdf[g]+=1.0/local;
}
}
mxy=getMean(r_pdf);
deltaxy=getVariance(r_pdf,mxy);
double deltaxy1=sqrt(deltaxy);
if(mxy<=mean*k0&&deltaxy1<=k2*delta1&&deltaxy1>=k1*delta1){
src.at(j,i)=src.at(j,i)*E;
}
}
}
}
int main(){
cv::Mat src=cv::imread("../1.png",0);
cv::Mat dst;
dst=src.clone();
histStatistic(dst,7,0.4,0.02,0.4,10);
cv::imshow("src",src);
cv::imshow("dst",dst);
cv::waitKey(0);
} 4.3 实现结果
代码参考:ps://www.cnblogs.com/brucemu/archive/2013/10/17/3374558.html