眼底视网膜血管增强方法（二）Gabor滤波

眼底视网膜血管增强方法（二）Gabor滤波

傅里叶变换自提出后被广泛地运用于信号、图像领域，但傅里叶变换是在整个时域进行分析，其变换到频域后丢失了原来的时域信息。对一整副图像进行傅里叶变换后，我们只能得到整副图像的频率分布情况，但很多时候我们是关心图像的局部频率分布，像边缘部分，这时傅里叶就无能无力了。为了使傅里叶具有局部特性，D.Gabor在1946年提出窗口傅里叶变换，即gabor变换。

Gabor变换的定义

为了同时获取信号的频域和时域信息，一个直观的做法就是给信号加一个窗函数，则此时傅里叶变换只对窗函数覆盖下的部分信号起作用，由此即可获得了局部信号的频域信息。
设f为具体函数，并且f(x)∈L2(R)，则窗口傅里叶变换（WFT）定义为

WFTf(w,b)=∫∞∞f(t)W(t−b)¯¯¯¯¯¯¯¯¯¯¯¯¯e−jwtdt

式中，W(t)为某一选定的窗函数。当W(t)为高斯函数时，则此时WFT就称为Gabor变换

Gf(a;w,b)=∫∞∞f(t)g∗a(t−b)e−jwtdt

其中， ga(t)=12π√δe−t22δ2 为一高斯窗函数。
如果把Gf(a;,b,w)对b进行积分，则有

g(w)=∫∞∞Gf(a;w,b)db

g(w)相当于f(t)经高斯平滑后的傅里叶变换。
Gabor逆变换表述为

f(t)=∬∞∞Gf(a;w,b)g∗a(t−b)ejwtdbdw

Gabor变换对眼底图像的增强

为了把Gabor变换用于图像领域，人们把Gabor函数推广到二维形式，形成的二维Gabor滤波器。二维Gabor滤波器在频域和空间域都具有最优的局部特性，能够很好地描述空间频率、空间位置和方向选择性等局部信息，同时对光照不敏感。神经科学家还发现，Gabor滤波器的响应和脊椎动物大脑视觉皮层的简单细胞响应非常相似。正是Gabor滤波非常适合用于图像的边缘检测，Soares1 等人把它用在眼底图像中进行特征提取。
设 x=[x1,x2]T∈R2 ，则二维Gabor滤波器定义为

ΨG(x,a)=exp(−jka−1x)exp(−12|Axa|2)

式中，A=diag[ε-1/2,1],ε≥1是一个对角矩阵，代表一个各项异性的高斯窗口，当ε=1时，为二维高斯窗口；k=[k1,k2]为不同方向的调制频率；a为一尺度因子。Gabor滤波器的显示图如图 1所示。
Gabor滤波器同样为方向各异性滤波器，类似于匹配滤波，为了在二维空间能得到最优响应，则必须考虑其方向与血管方向的相一致。文献[7]给出的做法是同样用一系列不同方向的滤波器模板来进行滤波操作，然后选取最大的响应作为输出。我们选取ε=1，k=[0,3]，方向选择18个不同方向，得到血管的增强图如图 2所示。

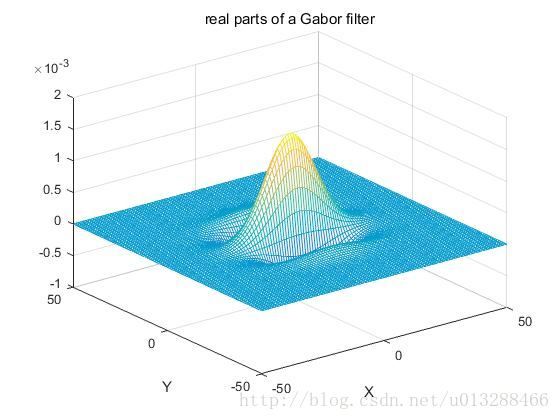
图1 Gabor滤波器的显示图

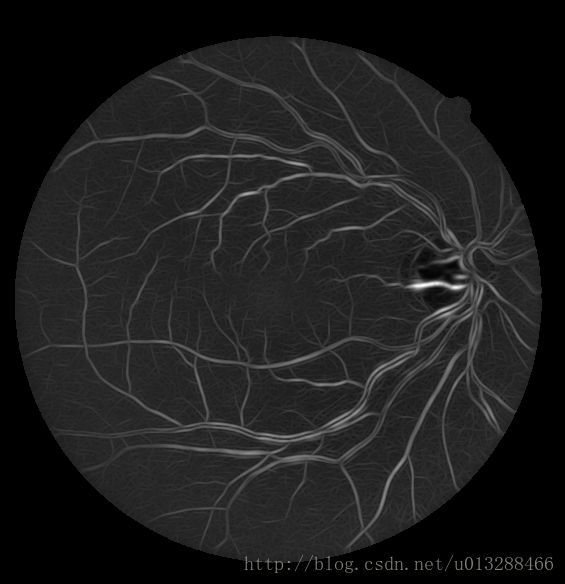
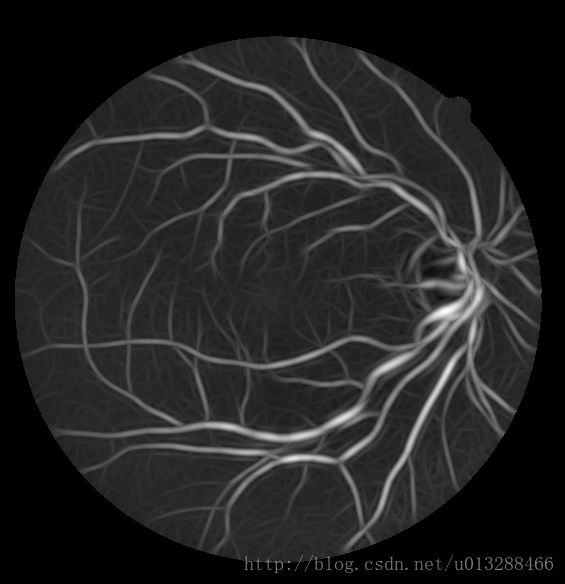
眼底血管Gabor滤波增强效果图, 左：尺度为2, 右：尺度为4

源码

    scales = [2,3,4,5];
    erosion = 5;
    [~, morlet] = generatemorletfeatures(img,mask,scales,erosion);
    morlet = morlet(:,:,2:end);
    for i=1:size(morlet,3)
        morlet(:,:,i) = normalize(morlet(:,:,i));
    end
    features = cat(3, features, morlet); 

完整代码包见http://download.csdn.net/detail/u013288466/9849447

---

1. Soares J V B, Leandro J J G, Cesar R M, et al. Retinal vessel segmentation using the 2-D Gabor wavelet and supervised classification[J]. IEEE Transactions on medical Imaging, 2006, 25(9): 1214-1222. ↩