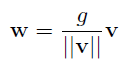关于深度网络中的Normalization:BN/RBN/WN/LN的记录
深度前馈网络中前层输入的变化往往会引起后面层的变化,后面的层需要不断地调整自己的参数去适应前层的输入变化,这被称为internal covariance shift。这不仅会使网络训练变得缓慢,同时会让一些非线性激活函数如sigmoid更容易进入饱和区。
传统的方法通过采用白化对样本进行预处理,让样本的特征之间独立同分布,来解决这个问题。如何对深度网络进行归一化?计算全部样本某个特征的均值与方差,对特征进行标准化。然而,这种做法往往计算量较大。有人提出了bacth normalization。首先,将每个batch的样本特征进行标准化。然而,通过简单的标准化,会导致改变原有参数的分布:网络后面的层努力调整自己的分布去适应前层的输入,标准化却让它丢失了自己的分布。因此,作者在标准化的基础上又提出了通过scale与bias两个参数将标准化后的数据还原成原来的分布。经过batch normalization,网络更加稳定。同时,batch normalization对每个batch样本进行相同的操作,使得网络不依赖于单个样本,因此也达到了一种正则化的效果。具体过程如下:
Batch normalization可以应用于卷积网络中。由于卷积网络中的每个feature map表示相同的特征,为了不改变卷积网络的原有性质,因此,在卷积网络中,每个feature map都有独立的scale与bias参数。
是否可以将batch normalization应用于rnn等循环神经网络呢。将rnn的每个时间步看成深度网络的每一层,即可以转化成前馈神经网络。那么,batch normalization也可以套用到rnn中了。然而,通过实验发现不同时间步之间共享均值与方差,效果并不是很好。在此基础上,有人提出了recurrent batch normalization。首先,既然时间步共享效果不好,那就不共享了,对每个时间步分别进行归一化。然而,测试时,万一训练集的最大时间步小于测试集的训练步呢。作者的方法也很简单,确定一个Tmax最大时间步,对超过最大时间步的测试集进行截断就可以了。同时,作者发现之前实验效果不行还存在另外一个原因,就是一般会将scale系数初始化为1。对于tanh激活函数,当输入的标准差越小,tanh的导数将会越接近于1。随着标准差增大,导数将会趋近于0,进入饱和区。因此,采用较小的scale参数,效果会更好。
深度网络往往是一个基于梯度下降的优化过程,优化的难易程度取决于海森矩阵的条件数,它反映了误差的曲面特征,如局部极小值、鞍点等,这样的网络往往受参数的影响较大。如何通过调整参数让网络更易训练?传统的做法在网络训练之前进行precondition,将梯度乘以一个fisher信息矩阵的逆,来模拟自然梯度,自然梯度可以让参数在变化相同的情况下,让目标值变化较大。类似的,batch normalization也是如此,它没有进行preondition,但它的过程可以类似于将fisher信息矩阵变为单位对角阵的过程。受到batch normalization的启发,同时为了解决batch normalization计算内存较大以及在rnn中不太适用的问题,有人提出了weight normalization。
Weight normalization也是一个将fisher信息矩阵对角化的重参数化的过程。Weight normalization将权重的更新分解为方向的更新与大小的更新,见公式2。它完成了两件事:1、对梯度的更新进行缩放,2、将梯度向量投影到权重向量之外。这样不仅可以使梯度的大小变化与权重的大小变化直接相关,同时由于投影,可以减少权重向量的噪声对梯度的影响。由于batch normalization能够固定每层网络输入特征的方差与均值,而weight normalization不可以,因此可以在初始化时将scale与bias参数初始为关于样本的方差与均值的函数。
同样为了解决rnn的正规化问题,有人提出了layer normalization。与之前的recurrent normalization对每个time step进行归一化不同的是,层归一化是对rnn纵向的归一化。与之前batch normalization或weight normalization不同的是,层归一化不是一个重新参数化的过程。 层归一化对每一层的输入的隐层单元进行标准化:同一层隐层单元采用相同的标准化,对于同一层的每个时间步采用相同的scale与bias参数,不同样本的隐层单元输入不同,因此进行不同的标准化,这样单个样本也可以进行标准化。
以上几种normalization,其实是互相联系的,它们都是对输入进行标准化,并进行scale与偏移,详见公式4。对于weight normalization,也是相同的形式,只是它的均值为0,方差为||V||。这几种normalization都有一定伸缩不变性,如权重伸缩不变性以及数据伸缩不变性,使网络训练更加迅速与稳定,减少对学习率的要求。
从参数空间的角度也可以理解这些normalization。模型学习到的参数可以形成一个光滑的流形空间,可以反映各种输入与输出的关系。如何衡量参数的变化引起输出分布的变化呢?将输出概率看作黎曼流形,通过参数变化前后输出概率的kl散度可以反映输出分布的变化。通过近似的泰勒展开式,可以得到当参数变化时,输出概率的分布变化近似于与fisher信息矩阵相关的参数变化。通过分析不同的normalization的fisher信息矩阵,其中normalize后的fisher信息矩阵由scale参数和方差变化控制。因此,当参数变化较大时,其输出的分布变化不会很大,训练会更加更稳定。同时,通过normalize,参数的变化主要由预测误差决定,而不经过normalize的网络训练主要由参数的范数决定。因此经过normalize后训练更加鲁棒。
[1] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
[2] RECURRENT BATCH NORMALIZATION
[3] Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks
[4] Layer Normalization
[5] https://zhuanlan.zhihu.com/p/33173246 详解深度学习中的Normalization,BN/LN/WN
[6] https://wenku.baidu.com/view/e050d42658fb770bf78a5525.html 自然梯度