多模式匹配算法-AC算法等
问题一:如果有一个关键词,然后让你在一段长文本中找出这些关键词,如何做?
问题二:如果有10K个关键词,然后让你在一段长文本中找出这些关键词,如何做?
如上问题一中,一段长文本中找一个关键词,那么就是单模式匹配。出了朴素算法(暴力算法)之外,还有一些经典的算法,例如KMP算法等。
问题二中,一段长文本中找N个关键词,那么就是多模式匹配,除了朴素算法外,也有一些经典的算法,例如AC算法、BM算法等。
这里主要讨论一下多模式匹配算法,也就是问题二。
模式匹配中,一般把原文本称为T(text,文本),关键词称为P(pattern,模式)。
1. 多模式匹配算法
1.1 AC算法
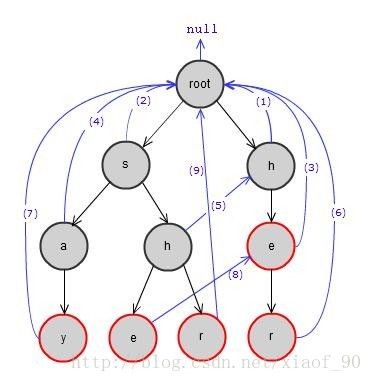
经典的AC算法,关键分为三个步骤:构成Trie树(生成goto表),构造失败指针(生成fail表),模式匹配(构造output表)。以下以模式串组为“say, she, shr, he, her”为例,做算法辅助说明。
构造Trie树
将每一个模式串逐字符添加进Trie树中。
Note:只考虑每一个词的跳转即可,从根起,合并相同的路径,直至出现同深度的不同字符为止。
结果如下图,红边框节点表示模式串结束节点:
节点的类如下:
class Node
{
Boolean isEnd;
short length;
Node fail;
Node[] next = new Node[27];
public Boolean IsEnd
{
get { return isEnd; }
set { isEnd = value; }
}
public short Length //计算column
{
get { return length; }
set { length = value; }
}
public Node Fail
{
get { return fail; }
set { fail = value; }
}
public Node[] Next
{
get { return next; }
set { next = value; }
}
}构造Trie树代码(只考虑小写字母和空格,理论上,ASCII码字符都支持):
static void Insert(string keyword, Node root)
{
Node p = root;
int index;
for (int i = 0; i < keyword.Length; i++)
{
if (keyword[i] == ' ')
{
index = keyword[i] - 6;
}
else
{
index = keyword[i] - 'a';
}
if (p.Next[index] == null)
{
p.Next[index] = new Node();
}
p = p.Next[index];
}
p.IsEnd = true;
p.Length = (short)keyword.Length;
}构造失败指针
对Trie树中每一个节点都生成Fail指针,表示从该节点开始出现不匹配的情况时,将按照Fail指针继续查找,保证搜索过的节点不会冗余搜索。对于某一个字母为A的节点(A1),沿着其父亲节点的Fail指针向上搜索,直到找到一个节点,它的子节点也包括字母为A(A2),就将A1的Fail指针指向A2。
Note:每一个节点都有Fail指针,root节点的Fail指针指向null,第1层节点(root节点属于第0层)的Fail指针指向root节点。
结果如下图,蓝实线表示Fail指针的指向:
构造失败指针的代码如下,其中:
static void BuildAutomation(Node root)
{
int head = 0;
int tail = 0;
List queue = new List();
queue.Add(root);
head++;
while (head != tail)
{
Node temp = queue[tail++];
Node p = new Node();
for (int i = 0; i < 27; i++)
{
if (temp.Next[i] != null)
{
if (temp == root)
{
temp.Next[i].Fail = root;
}
else
{
p = temp.Fail;
while (p != null)
{
if (p.Next[i] != null)
{
temp.Next[i].Fail = p.Next[i];
break;
}
p = p.Fail;
}
if (p == null)
{
temp.Next[i].Fail = root;
}
}
queue.Add(temp.Next[i]);
head++;
}
}
}
} 以图 - 1为基础,由图 - 2详细说明如何生成Fail指针:
- root节点的Fail指针指向null,入队,进入循环。
- 第1次循环,处理第1层的2个节点:root.Next[‘h’-‘a’]和root.Next[’s’-‘a’]。把2个节点的Fail指针指向root,并先后进入队列。得到的Fail指针指向为图 - 2中(1)(2)。
- 第2次循环,先从队列中取出h,然后p指向h节点的Fail指针所指向的节点,即root节点,此时temp为h节点,因为p.Next[‘e’-‘a’](即root.Next[‘e’-‘a’])为null,所以执行p = p.Fail。得到的Fail指针指向为图 - 2中(3),e节点进入队列。
- 第3次循环,从队列中取出s节点,与第2次循环类似,temp为s节点,得到的Fail指针如图 - 2中(4),a节点进入队列。接下来处理h节点时,因为temp.Fail为root,并且root.Next[‘h’-‘a’]不为null,所以把第2层的h节点的Fail指针指向第1层h节点,得到如图 - 2中(5),h节点进入队列。
- 以此类推,在循环结束后,所有Fail指针的指向如图 - 2所示。
模式匹配
匹配过程分两种情况:
(1) 当前字符匹配,表示从当前节点沿着树边有一条路径可以到达目标字符,此时只需沿该路径走向下一个节点继续匹配即可,目标字符串指针移向下个字符继续匹配;
(2) 当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,匹配过程随着指针指向root结束。重复这2个过程中的任意一个,直到匹配串走到结尾为止。
模式匹配代码如下:
static void Match(Node root)
{
int numReturn = 0;
int numCurrentLineChar = 0;
int index = 0;
Node p = root;
TestResult result = new TestResult();
for (int i = 0; i < content.Length; i++)
{
if (content[i] == '\n')
{
numReturn++;
numCurrentLineChar = 0;
p = root;
continue;
}
else if (content[i] == ' ')
{
index = content[i] - 6;
}
else if (content[i] >= 'a' && content[i] <= 'z')
{
index = content[i] - 'a';
}
else
{
continue;
}
numCurrentLineChar++;
while (p.Next[index] == null && p != root)
{
p = p.Fail;
}
p = p.Next[index];
p = (p == null) ? root : p;
Node temp = p;
while (temp != root && temp.IsEnd)
{
result.ResultList.Add(new TestResultUnit(numReturn, numCurrentLineChar - temp.Length));
temp = temp.Fail;
}
}
}算法的遗漏
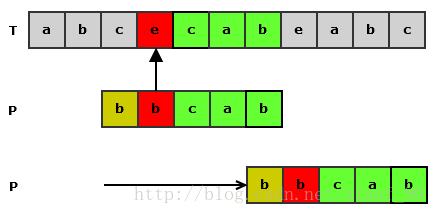
但是,经典的AC算法,并没有包括不断词的情况,例如,匹配串“abcdefg”,模式串组“abc, bc, b”,按照该AC自动机,当遇到abc模式串时,直接匹配成功,就不再匹配出bc和b。
针对此问题,在模式匹配步骤中,加入以下逻辑:若当下节点的Fail指针指向的是除root节点之外的节点(即第1层及以下层的节点),会从该节点开始,沿Fail节点向上搜索,直到找到root节点为止,记录所有找到某模式串结束字符的节点。
修正不断词情况的代码如下:
Node tmp = p;
while (tmp.Fail != root && tmp != root)
{
tmp = tmp.Fail;
if (tmp.IsEnd)
{
resultList.Add(new TestResultUnit(this.Id, numReturn, numCurrentLineChar - tmp.Length, resultType));
}
else
{
continue;
}
}以上面的例子为例,得到的带Fail指针的Trie树如下图:
按照模式匹配的规则,当匹配到第2层的b节点时,b.Fail!=root,所以从b节点开始,沿Fail节点向上找到root为止,其中第1层的b为模式串b的结束字符,所以匹配到匹配串b,之后,依次匹配出来的模式串为abc,bc。
1.2 BM算法
BM算法是一种单模式匹配算法,之所以在这里讨论它,是因为有一种对AC算法的改进算法,使用到了BM算法。
BM算法采用从右向左比较的方法,同时使用了两种启发式规则:坏字符规则和好后缀规则,来决定向右跳跃的距离。向右跳跃的距离为坏字符规则和好后缀规则计算结果的最大值。
设匹配串为T串,模式串为P串。
坏字符规则
从右到左的扫描过程中,发现 Ti 与 Pj 不同:
(1)如果P 中存在一个字符 Pk 与 Ti 相同,且 k
static void BadCharactor(int[] badCharactor, string pattern)
{
for (int i = 0; i < ALPHABET_LEN; i++)
{
badCharactor[i] = pattern.Length;
}
for (int i = 0; i < pattern.Length - 1; i++)
{
badCharactor[pattern[i]] = pattern.Length - 1 - i;
}
}好后缀规则
从右到左的扫描过程中,发现 Ti 与 Pj 不同,检查一下相同的部分 t 是否在 P 中的其他位置 t’ 出现:
(1) 如果 t 与 t’ 的前一个字母不相同,就将 P 向右移,使 t’ 与 T 中的 t 对齐。
(2) 如果 t’ 没有出现,则找到与 t 的后缀相同的 P 的最长前缀 x,向右移动P ,使 x 与 T 中 t 的后缀相对应。
Note:情况(1)中,t’与t的前一个字母必须不相同,不然t’不存在,属于情况(2)。
好后缀匹配代码如下:
static void GoodSuffix(List<int> goodSuffix, string pattern)
{
int lastPrefixIndex = pattern.Length - 1;
for (int i = pattern.Length - 1; i >= 0; i--)
{
if (Is_Prefix(pattern, i + 1))
{
lastPrefixIndex = i + 1;
}
goodSuffix[i] = lastPrefixIndex + (pattern.Length - 1 - i);
}
for (int i = 0; i < pattern.Length - 1; i++)
{
int sLen = SuffixLength(pattern, i);
if (pattern[i - sLen] != pattern[pattern.Length - 1 - sLen])
{
goodSuffix[pattern.Length - 1 - sLen] = pattern.Length - 1 - i + sLen;
}
}
}
static bool Is_Prefix(string word, int pos)
{
int suffixLen = word.Length - pos;
for (int i = 0; i < suffixLen; i++)
{
if (word[i] != word[pos + i])
{
return false;
}
}
return true;
}
static int SuffixLength(string word, int pos)
{
int i = 0;
for (i = 0; i < pos && word[pos - i] == word[word.Length - 1 - i]; i++) ;
return i;
}匹配过程的代码如下:
static List<int> BmSerach(string textString, string pattern)
{
List<int> resultList = new List<int>();
int i = 0;
int[] badCharactor = new int[255];
List<int> goodSuffix = new List<int>();
for (i = 0; i < pattern.Length; i++)
{
goodSuffix.Add(0);
}
BadCharactor(badCharactor, pattern);
GoodSuffix(goodSuffix, pattern);
i = pattern.Length - 1;
while (i < textString.Length)
{
int j = pattern.Length - 1;
while (j >= 0 && textString[i] == pattern[j])
{
i--;
j--;
}
if (j < 0)
{
resultList.Add(i + 1);
i += pattern.Length + 1;
continue;
}
i += (badCharactor[textString[i]] < goodSuffix[j] ? goodSuffix[j] : badCharactor[textString[i]]);
}
return resultList;
}以下还有一些多模式匹配算法,有些只知其名,没有细究,顺便把这些也都一并列举出来吧
1.3 改进的AC-BM算法
AC-BM算法将待匹配的字符串集合转换为一个类似于AC算法的树状有限状态机,但构建时不是基于字符串的后缀而是前缀。匹配时,采用自后向前的方法,并借用BM算法的坏字符规则和好后缀规则。
1.4 AC和QS结合的反向自动机
反向自动机多模式匹配算法,且针对纯中文的处理算法。
1.5 DAWG-MATCH
是一种后缀自动机,是建立在模式集P上,能够辨认出模式集P上所有关键字后缀的确定型自动机。主要是AC和RF的结合结果。
1.6 SumKim99
一种使用HashTable和Bit-Parallel的算法。他的处理过程比较特别,先对模式数值化压缩存储,然后使用HashTable直接定位出当前读入的字符将可能匹配上的关键字的范围,接着再用位运算对可能匹配上的关键字逐个比较,判定文本中是否有关键字出现。
1.7 MAC算法
2. 适用于大规模的多关键字匹配的多模匹配算法
2.1 agrep
对处理大规模的多关键字匹配问题有高效。多模式中最著名的快速匹配算法之一。
2.2 MultiBDM
基于AC和DAWG两种自动机扫描思想的多模匹配算法。根据匹配过程中使用时可的不同,作者提出了两种改进。