【论文】A Comprehensive Survey on Graph Neural Networks

Qustion：The data in these tasks are typically represented in the
Euclidean space. However, there is an increasing number of applications where data are generated from non-Euclidean domains and are represented as graphs with complex relationships and interdependency between objects. The complexity of graph data has
imposed significant challenges on existing machine learning algorithms.

Solution：Recently, many studies on extending deep learning
approaches for graph data have emerged.

Contribution：

1. We provide a comprehensive overview of graph neural networks (GNNs) in data mining and machine learning fields.
2. We propose a new taxonomy to divide the state-of-the-art graph neural networks into different categories.
3. With a focus on graph convolutional networks, we alternative architectures that have recently been developed; these learning paradigms include graph attention networks, graph autoencoders, graph generative networks, and graph spatial-temporal networks.
4. We further discuss the applications of graph neural networks across various domains and summarize the open source codes and benchmarks of the existing algorithms on different learning tasks.
5. Finally, we propose potential research directions in this fast-growing field.

问题：图数据包含真实世界的复杂关系和相互依赖。传统的机器学习方法不适合处理这类数据。

解决：近年来，对图数据深度学习方法的扩展研究越来越多。

贡献：

1. 图卷积网络（GNNs）的综述
2. GNNs的分类
3. 回顾GNNs和其他图网络架构（GAT，图自编码器，图生成网络，图时空网络）
4. 讨论GNNs在不同领域的应用
5. 未来有潜力的研究方向

1 Introduction

尽管深度学习在欧几里得数据上取得了巨大的成功，但越来越多的应用程序需要对非欧几里得域生成的数据进行有效的分析。每个图都有一个可变大小的无序节点，图中的每个节点都有不同数量的邻居，这就导致了一些重要的操作(如卷积)，这些操作在图像域中很容易计算，但不再直接适用于图域。

借鉴传统的卷积网络、循环网络、自编码器网络，针对图数据设计图神经网络的架构。

GNN历史

年份	主要作者	文章	备注
2005 IJCNN	Gori	A new model for learning in graph domains	First outline
2009 ITNN	Scarselli	The graph neural network model	Further elaborated
2015 ICLR	Li	Gated graph sequence neural networks	Computation Efficiency
2018 ICML	Dai	Learning steady-states of iterative algorithms over graphs	Computation Efficiency
2014 ICLR	Bruna	Spectral networks and locally connected networks on graphs	First prominent research on spectral-based GNNs
2016 NIPS	Defferrard	Convolutional neural networks on graphs with fast localized spectral filtering	Improvement on (2014 ICLR)
2017 ICLR	Kipf	Semi-supervised classification with graph convolutional networks	Improvement on (2014 ICLR)
2015 arXiv	Henaff	Deep convolutional networks on graph-structured data	Improvement on (2014 ICLR)
2018 AAAI	R. Li	Adaptive graph convolutional neural networks	Improvement on (2014 ICLR)
2017 arXiv	Levie	Cayleynets:Graph convolutional neural networks with complex rational spectral filters	Improvement on (2014 ICLR)
2017 NIPS	Hamilton	Inductive representation learning on large graphs	Spacial-based GNNs
2017 CVPR	Monti	Geometric deep learning on graphs and manifolds using mixture model cnns	Spacial-based GNNs
2016 ICML	Niepert	Learning convolutional neural networks for graphs	Spacial-based GNNs
2018 SIGKDD	Gao	Large-scale learnable graph convolutional networks	Spacial-based GNNs

图神经网络相关综述

年份	主要作者	文章	备注
2017 SPM	Bronstein	Geometric deep learning: going beyond euclidean data	第一篇GCN综述，但是缺少对一些spacial-based GCN和GCN之外的其他方法的描述。
2018 arXiv	Battaglia	Relational inductive biases, deep learning, and graph networks	使用building block统一地描述GNN，缺点是有点抽象
2018 arXiv	Lee	Attention models in graphs: A survey	图注意网络的综述
2018 arXiv	Zhang	Deep learning on graphs: A survey	缺少图生成网络（graph generative network）时空网络（spatial-temporal network）

Graph Nerual Network vs. Network Embedding

Network embedding：

1. aims to represent network vertices into a low-dimensional vector space,
2. by preserving both network topology structure and node content information,
3. so that any subsequent graph analytics tasks such as classification, clustering, and recommendation can be easily performed by using simple off-the-shelf learning machine algorithm.
4. Many network embedding algorithms are typically unsupervised algorithms and they can be broadly classified into three groups [32], i.e., matrix factorization [38], [39], random walks [40], and deep learning approaches.

贡献

1. New taxonomy（5 categories：GCNs, GATs, GAEs, GGNs, GSTNs）
2. Comprehensive review（description, comparison, summarization）
3. Abundant resources（algorithms, datasets, codes, applications）
4. Future directions

Section 2 defines a list of graph-related concepts.
Section 3 clarifies the categorization of graph neural networks.
Section 4 and Section 5 provides an overview of graph neural network models.
Section 6 presents a gallery of applications across various domains.
Section 7 discusses the current challenges and suggests future directions.
Section 8 summarizes the paper.

2 Definition

Graph：$G=(A,X),A\in R^{N\times N},X\in R^{N\times D}$
Directed Graph：$A_{ij}\ne A_{ji}$
Spatial-Temporal Graph：$G=(A,X),A\in R^{N\times N},X\in R^{T\times N\times D}$

3 Categorization

不同分类的代表著作：

GNN分类

GCN
关键是学习到一个函数f，f能够把每个节点及其相邻结点的特征聚集起来，目标输出是节点的真实标签。GCN是很多其他GNN的基础构件。

GAT
在GCN的基础上加上权重参数，使得更重要的node、walk、model有更大的权重。权重参数是和网络其他参数在同一个端到端模型下训练得到的。

GAE

aim to learn a low dimensional node vectors via an encoder
reconstruct the graph data via a decoder.

encoder: graph structure -> node vectors
decoder: node vectors -> graph structure

对于无属性图（plain graph），可以直接处理邻接矩阵，生成一个新的矩阵（pointwise mutual information matrix），或者把邻接矩阵输入一个autoencoder，获取第一序和第二序信息。

对于属性图（attributed graph）：把GCN作为building block构建encoder（为每个节点生成低维向量），使用连接预测作为decoder重构图的结构（为每一对节点重新生成边）

GGN

从数据中生成接近真实世界的（plausible）图。GGN需要给出一个图的经验分布，这是一个很有挑战的任务，因为图是复杂的数据结构。为了解决这一问题，提出了按节点生成图、按边生成图等方法。

一个应用是在化学分子领域，原子视为图的节点，化学键视为图的边，生成的图可以用于发现具有特定性质的新化学分子。

GSTN

aim to learn unseen patterns from spatial-temporal graphs（在交通预测、人体行为预测等方面有重要应用）

例如，道路交通网络是一个自然的图，其中每个关键位置是一个节点，其交通数据被连续监控。通过建立有效的图数据时空网络模型，可以准确预测整个交通系统的交通状态[70]，[71]。

图时空网络的关键思想是同时考虑空间依赖性和时间依赖性。目前的许多方法都是利用GCNs和一些RNN[70]或CNN[71]来捕获依赖关系，对时间依赖关系进行建模。

框架

图神经网络，特别是图卷积网络(GCNs)，试图通过图谱理论或空间局部性定义图卷积，复制CNN在图像数据方面的成功。以图结构和节点内容信息为输入，GCN有多种输出，分别对应不同的图分析任务：

• Node-Level：输出与节点回归和分类任务相关。由于图数据卷积模块直接给出了节点的潜在表示，因此GCN的最后一层是多感知器层或软最大值层。
• Edge-Level：输出与链接预测任务相关。为了预测边缘的标签/连接强度，一个额外的函数将从图卷积模块中获取两个节点的潜在表示作为输入。
• Graph-Level：输出与图分类任务相关。为了在图层次上获得紧凑表示，使用池模块将图粗化为子图，或对节点表示进行求和/平均。

根据at hand的学习任务和标签信息，使用一个端到端的框架，通过监督（半监督）甚至无监督的方式，对GCN进行训练。

• Semi-Supervised for node classification：图卷积网络可以学习一个有效的模型，识别未标记节点的类标签。为此，可以通过叠加几层图卷积层和一个多分类的softmax层来构建端到端框架。
• Supervised for graph classification：给定一个图数据集，图级分类旨在预测整个图的类标签。该任务的端到端学习可以使用一个框架来完成，该框架结合了图形卷积层和池化过程。具体来说，通过应用图卷积层，我们得到了每个图中每个节点维数固定的表示形式。然后，我们可以通过汇聚图中所有节点的表示向量，从而得到整个图的表示。最后，通过应用现有深度学习框架中常用的MLP层和softmax层，我们可以构建一个端到端的图分类框架。
• Unsupervised for graph embedding：当图中没有可用的类标签时，我们可以在端到端框架中以完全无监督的方式学习图嵌入。这些算法以两种方式处理边信息。一种简单的方法是采用一种自动编码器框架，其中编码器使用图形卷积层将图嵌入潜在表示中，然后使用解码器重构图结构[59]，[61]。另一种方法是采用负采样方法，即对节点对的一部分进行负采样，而对图中已有节点对的链接进行正采样。然后在卷积层之后应用逻辑回归层进行端到端学习[24]。

4 GCN

在这一节中，我们回顾图卷积网络(GCNs)，它是许多复杂的图神经网络模型的基础。GCNs方法分为两类，基于频谱的和基于空间的。基于频谱的方法通过从图信号处理的角度引入滤波器来定义图卷积[76]，其中图卷积运算被解释为从图信号中去除噪声。基于空间的方法将图卷积表示为邻居的特征信息聚合。虽然GCNs操作在节点级，但是图数据池模块可以与GCN层交错，从而将图数据粗化为高级的子结构。如图5a所示，这种架构设计可以用来提取图级表示，并执行图分类任务。接下来，我们将分别介绍基于频谱的GCNs、基于空间的GCNs和图池模块。

4.1 基于频谱的GCNs

基于频谱的方法在图信号处理方面具有坚实的基础[76]。首先介绍了图信号处理的基本知识背景，然后回顾了基于频谱的GCNs的代表性研究。

4.1.1 背景

图的一个健壮的数学表示是归一化图拉普拉斯矩阵（normalized graph Laplacian matrix）：
$$L=I_n-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$
其中D是节点度矩阵（对角矩阵）：
$$D_{ii}=\sum _j{A}_{i,j}$$

归一化图拉普拉斯矩阵具有实对称正半定的性质，因此可以被特征分解为：
$$L=U\Lambda U^T$$
其中$U$是特征向量组成的矩阵，$\Lambda$是特征值对角矩阵。

特征向量矩阵$U$构成了一个标准正交空间，用数学语言说就是：$U^{T}U=I$. 在图信号处理领域，一个图有$N$个节点，每个节点有一个值，$N$个值组成一个向量$x\in R^N$就称为一个图信号。对于图信号，我们可以在其上定义傅里叶变换和逆傅里叶变化：

$$\mathcal{F}(x)=U^{T}x=\hat{x}$$
$${\mathcal{F}}^{-1}(\hat{x})=\hat{x}U$$

为了理解图的傅里叶变换，从它的定义我们可以看到它确实将输入的图信号投射到正交空间中，在这个空间中基是由归一化图拉普拉斯变换的特征向量构成的。被转换后的信号$\hat{x}$就是图信号在新的特征向量空间$U$中的坐标，所以初始的图信号可以表示为$x={\sum }_i{\hat{x}}_i{u}_i$，这恰好就是逆傅里叶变换所做的事。

现在有了傅里叶变换$\mathcal{F}$和逆傅里叶变换${\mathcal{F}}^{-1}$，输入图信号$x\in R^N$，以及过滤器$g\in R^N$，我们可以定义图卷积操作 $\ast$：

$$x\ast g={\mathcal{F}}^{-1}(\mathcal{F}(x)\odot \mathcal{F}(g))=U{U}^{T}x\cdot diag(U^{T}g)$$

$\odot$表示按元素相乘（Hadamard product），其中$diag(U^{T}g)$和$g$存在一一对应关系，定义$g_{\theta }=diag(U^{T}g)$可以将公式简化为：

$$x\ast g=U{g}_{\theta }{U}^{T}x$$

基于频谱的图卷积都可以如此通用地表示，区别只在于$g_{\theta }$的选择。

4.1.2 方法

• Spectral CNN：
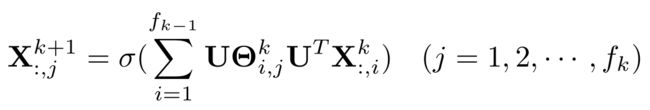
• ChebNet：
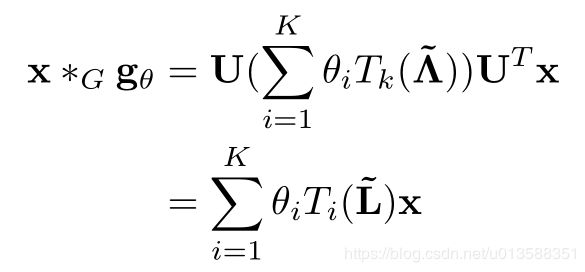
• First order of ChebNet：
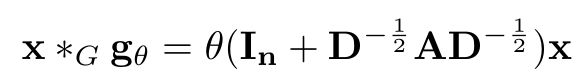
• Adaptive Graph Convolution Network (AGCN)：AGCN augments a graph with a so-called residual graph, which is constructed by computing a pairwise distance of nodes.

4.1.3 总结

频谱CNN[20]依赖于拉普拉斯矩阵的特征分解。它有三个影响。首先，对图的任何扰动都会导致特征基的改变。其次，所学习的过滤器是与域相关的，这意味着它们不能应用于具有不同结构的图。第三，特征分解需要O(n3)计算和O(n2)内存。由ChebNet[12]和1stChebNet[14]定义的过滤器定位在空间中。学习到的权重可以在图中的不同位置共享。然而，谱方法的一个常见缺点是需要将整个图加载到内存中进行图形卷积，在处理大的图时效率不高。

4.2 基于空间的GCNs

模拟传统的卷积神经网络对图像的卷积运算，基于空间的方法定义基于节点空间关系的图卷积。为了将图像与图联系起来，可以将图像看作一种特殊的图形式，每个像素代表一个节点。

在图像中，由于相邻节点的顺序是特定的，因此可以在不同的位置共享可训练的权重（过滤器）。类似地，对于一般图，基于空间的图卷积将中心节点表示及其邻居表示进行聚合，得到该节点的新表示。 为了探索节点的感受野的深度和广度，常见的做法是叠加多个图卷积层。根据叠加方法的不同，基于空间的GCN可以进一步分类为recurrent-based（使用同一个卷积层迭代更新得到隐藏表示）和composition-based（使用不同卷积层）方法。在下面,我们给出这两个分支的概述。

4.2.1 Recurrent-based Spatial GCNs

递归方法的主要思想是递归地更新一个节点的潜表示，直到达到一个稳定的不动点。这是通过对递归函数[17]施加约束、使用门递归单位结构（ gate recurrent unit）[18]、随机异步更新节点潜在表示[19]来实现的。下面，我们将介绍这三种方法。

• Graph Neural Networks(GNNs)：在图神经网络中，递归更新节点潜在表示直到收敛，是最早的方法之一。换句话说，从扩散过程来看，每个节点与相邻节点交换信息，直到达到均衡。为了保证收敛，递归函数f(·)必须是一个收缩映射，在映射后收缩两点之间的距离。如果f(·)是神经网络，则必须对参数的雅可比矩阵施加惩罚项。GNNs采用almeeda - pineda算法[77]、[78]训练其模型。其核心思想是运行传播过程以达到固定点，然后在给定收敛解的情况下执行反向过程。
• Gated Graph Neural Networks (GGNNs)：GGNNs采用门控递归单元(GRU)[79]作为递归函数，将递归减少到固定的步长。与GNNs不同，GGNNs使用时间反向传播(BPTT)来学习参数。它的优点是不再需要约束参数来保证收敛性。然而，BPTT训练的缺点是它牺牲了时间和记忆的效率。这对于大型图尤其有问题，因为GGNNs需要在所有节点上多次运行递归函数，要求所有节点的中间状态都存储在内存中。
• Stochastic Steady-state Embedding (SSE)：为了提高学习效率，SSE算法[19]以异步方式随机更新节点的潜在表示。如算法1所示，SSE递归估计节点潜在表示，并用采样的批处理数据更新参数。为了保证收敛到稳定状态，SSE的递归函数被定义为历史状态和新状态的加权平均值。虽然对邻域信息的求和隐含了节点度的概念，但是对邻域信息求和的规模是否会影响算法的稳定性还存在疑问。

4.2.2 Composition-Based Spatial GCNs
基于组合的方法通过叠加多个图卷积层来更新节点表示。

• Message Passing Neural Networks (MPNNs)：Gilmer等人[13]将现有的几个图卷积网络，包括[12]、[14]、[18]、[20]、[53]，[80]、[81]归纳为一个统一的框架，命名为消息传递神经网络(Message Passing Neural networks, MPNNs)。MPNNs由两个阶段组成，消息传递阶段和读出阶段。消息传递阶段实际上是基于T步空间的图卷积。通过消息函数$M_t(\cdot )$和更新函数$U_t(\cdot )$定义图的卷积运算。读出阶段实际上是一个池操作，它根据每个节点的隐藏表示生成整个图的表示。通过输出函数$R(\cdot )$，得到最终表示$\hat{y}$来执行图级预测任务。作者通过假设$U_t(\cdot )$和$M_t(\cdot )$的不同形式，提出了其他几个图卷积网络也属于它们的框架。
  
  

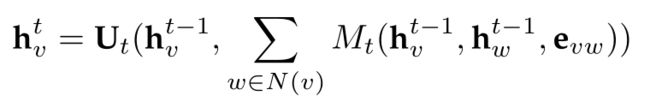
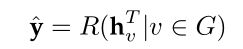
• GraphSage：引入聚合函数的概念来定义图卷积。聚合函数本质上是集合一个节点的邻域信息。它必须是一个节点序无关的函数（如均值、求和和最大函数）。图的卷积运算定义为：
  
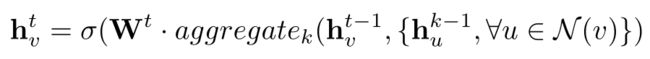
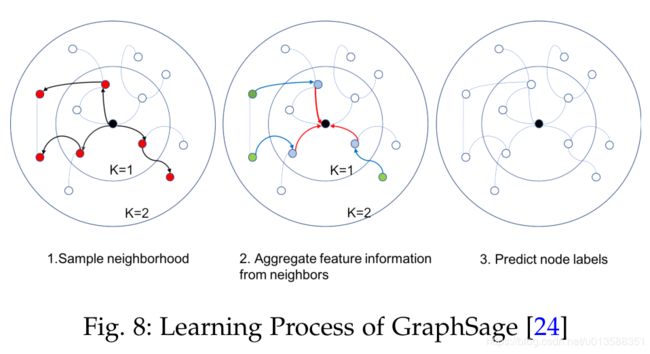
  GraphSage没有更新所有节点的状态，而是提出了一种批量训练算法，提高了大型图的可伸缩性。特征的学习过程包括三个步骤。首先，它对一个固定大小的节点的本地k-hop邻居进行采样。其次，通过聚集相邻节点的信息特征，得到中心节点的最终状态。最后，利用中心节点的最终状态进行预测和反向传播。这个过程如图8所示。
  

4.2.3 Miscellaneous Variants of Spatial GCNs

• Diffusion Convolution Neural Networks (DCNN)：扩大节点的邻居感受野，通过一个概率转移矩阵确定每个节点的转移概率。
• PATCHY-SAN：使用标准卷积神经网络(CNN)来解决图的分类任务。为此，它将图形结构的数据转换为网格结构的数据。
• Large-scale Graph Convolution Networks (LGCN)：对于每个节点，LGCN将其邻近域的特征矩阵集合起来，并沿着每一列对该特征矩阵进行排序。将排序后的特征矩阵的前k行作为目标节点的输入网格数据。最后，LGCN对合成的输入应用1D CNN，得到目标节点的隐藏表示。
• Mixture Model Network (MoNet)：MoNet引入伪坐标和权函数，通过节点与其邻居之间的相对位置(伪坐标)来确定节点邻居的权值。提出了一个具有可学习参数的高斯核函数来自由调整权函数。

4.2.4 总结

基于空间的方法通过聚集邻居的特征信息来定义图卷积。根据图形卷积层的不同叠加方式，将基于空间的方法分为两类:基于递归的方法和基于合成的方法。基于递归的方法试图获得节点的稳定状态，而基于组合的方法试图合并更高阶的邻域信息。在每个层中，两个组都必须在训练期间更新所有节点上的隐藏状态。然而，它不是有效的，因为它必须将所有中间状态存储到内存中。为了解决这个问题，提出了几种培训策略，包括针对基于组合的方法(如GraphSage[24])的子图训练，以及针对基于递归的方法(如SSE[19])的随机异步训练。

4.3 池模块

在将卷积神经网络推广到图数据结构时，另一个关键组件图池模块也至关重要，特别是对于图级分类任务[55]、[56][87]。Xu等人[88]认为，在区分图结构方面，有池模块的GCNs与weisfeler-lehman检验[82]一样强大。与CNNs自带的原始池化层类似，图池化模块通过对原始特征数据进行下采样，可以很容易地降低方差和计算复杂度。均值/最大值/和池是实现这一目标的最原始和最有效的方法，因为计算池窗口中的均值/最大值/和值非常迅速。

Henaff等人的[21]证明了在网络开始时执行一个简单的max/mean池对于降低图域的维数和降低昂贵的图的傅里叶变换操作的成本是非常重要的。

Defferrard等人在他们的方法ChebNet[12]中优化了最大/最小池和设备的有效池策略。输入图首先经过图5a所述的粗化处理。在粗化之后，将输入图的顶点及其粗化后的版本在一个平衡的二叉树中进行重构。在最粗的层次上对节点进行任意排序，然后将这种排序传播到平衡二叉树的较低层次上，最终会在最细的层次上产生一个规则的排序。汇集这样一个后置的一维信号比原来的信号要有效得多。

Zhang等人还提出了一个框架DGCNN[55]，该框架采用了一种类似的池策略，名为SortPooling，通过将顶点重新排列到有意义的顺序来执行池。与ChebNet[12]不同，DGCNN根据顶点在图中的结构角色对其进行排序。空间图卷积中的图的无序顶点特征被视为连续的WL颜色[82]，然后它们被用来对顶点排序。除了对顶点特征进行排序外，还通过聚合/扩展图s特征张量将图的大小统一到k。如果n > k，则删除最后的n k行，否则将添加k n 0行。该方法通过解决一个称为置换不变量的底层图结构任务，增强了池网络，提高了GCNs的性能。Verma和Zhang提出了图包网[89]，进一步探讨了图数据的排列不变式。

DIFFPOOL[56]通过使用两个gnn来聚簇节点，重新定义了图形池模块。任何标准的GCN模块都可以与DIFFPOOL相结合，不仅可以提高性能，还可以加速卷积运算。

4.4 频谱 vs. 空间

频谱模型作为最早的图形数据卷积网络，在许多图形分析任务中取得了令人瞩目的成绩。这些模型在图形信号处理方面具有一定的理论基础。通过设计新的图信号滤波器[23]，理论上可以设计出新的图卷积网络。然而，基于光谱的模型有几个缺点。我们从效率、通用性、灵活性三个方面进行了阐述。

在效率方面，基于频谱的模型的计算成本随着图的大小而急剧增加，因为它们要么需要执行特征向量计算[20]，要么需要同时处理整个图，这使得它们难以并行或扩展到大规模图。 基于空间的模型具有处理大型图的潜力，因为它们通过聚集邻居节点直接在图域中执行卷积。 可以在一批节点而不是整个图中执行计算。 当相邻节点的数量增加时，可以开发采样技术[24]，[27]以提高效率。

在通用性方面，基于频谱的模型假设了一个固定的图，这使得它们很难推广到新的或不同的图。另一方面，基于空间的模型在每个节点上局部地执行图卷积，在不同的位置和结构之间可以轻松地共享权重。

在灵活性方面，基于频谱的模型仅限于在无向图上工作。有向图上的拉普拉斯矩阵没有明确的定义，因此将基于频谱的模型应用于有向图的唯一方法是将有向图转换为无向图。基于空间的模型更灵活地处理多源输入，如边缘特征和边缘方向，因为这些输入可以合并到聚合函数中(如[13]、[17]、[51]、[52]、[53])。

因此，近年来空间模型受到越来越多的关注[25]。

5 Beyond GCN

在这一节中，我们回顾其他的图神经网络，包括图注意神经网络、图自动编码器、图生成网络和图时空网络。在表4中，我们对每个类别下的主要方法进行了总结。

5.1 Graph Attention Networks

注意机制几乎已经成为基于序列的任务的标准[90]。 注意机制的优点是它们专注于对象最重要部分的能力。 该专业已被证明可用于许多任务，例如机器翻译和自然语言理解。 由于注意力机制的模型容量增加，图神经网络还可以通过在聚合过程中使用注意力，集成多个模型的输出以及生成面向重要性的随机游走而从中受益。 在本节中，我们将讨论在图结构化数据中如何使用注意力机制。

5.1.1 方法

• Graph Attention Network (GAT)：
• Gated Attention Network (GAAN)：
• Graph Attention Model (GAM)：
• Attention Walks：

5.1.2 总结

注意机制对图神经网络的贡献有三种不同的方式，即在聚集特征信息时对不同的邻居分配注意权值，根据注意权值对多个模型进行集合，利用注意权值引导随机游动。尽管GAT[15]和GAAN[28]被归为图注意网络的范畴，但它们同时也可以被认为是基于空间的图卷积网络。GAT[15]和GAAN[28]的优点是可以很好的学习邻居的重要性权重，如图6所示。然而，由于必须计算每一对邻居之间的注意权值，计算成本和内存消耗迅速增加。

5.2 Graph Auto-encoders

图数据自动编码器是一种利用神经网络结构将网络顶点表示成低维向量空间的网络嵌入方法。典型的解决方案是利用多层感知器作为编码器来获得节点嵌入，其中解码器重构节点的邻域统计信息，如正点互信息(PPMI)[41]或一、二阶近似[42]。最近，研究人员探索了利用GCN[14]作为编码器，将GCN[14]与GAN结合[91]，或将LSTM[7]与GAN结合[91]来设计图形自动编码器。我们将首先审查基于GCN的自动编码器，然后总结其他变种在这个类别。

5.2.1 GCN Based Auto-encoders

• Graph Auto-encoder (GAE)：
• Adversarially Regularized Graph Autoencoder (ARGA)

5.2.2 Miscellaneous Variants of Graph Auto-encoders

• Network Representations with Adversarially Regularized Autoencoders (NetRA)：
• Deep Neural Networks for Graph Representations(DNGR)：
• Structural Deep Network Embedding (SDNE)：
• Deep Recursive Network Embedding (DRNE)：

5.2.3 总结

DNGR和SDNE仅在给出拓扑结构的情况下学习节点嵌入，而GAE，ARGA，NetRA，DRNE在拓扑信息和节点内容特征均可用时学习节点嵌入。 图自动编码器的一个挑战是邻接矩阵A的稀疏性，导致解码器的正项数量远远少于负数。 为解决此问题，DNGR重建了一个更密集的矩阵，即PPMI矩阵，SDNE对邻接矩阵的零项施加了惩罚，GAE对邻接矩阵中的项进行了加权，并且NetRA将图线性化为序列。

5.3 Graph Generative Networks

图生成网络的目标是给定一组观察到的图来生成图。 图形生成网络的许多方法都是特定于领域的。 例如，在分子图生成中，一些作品对称为SMILES [94]，[95]，[96]，[97]的分子图的字符串表示进行建模。 在自然语言处理中，通常以给定的句子为条件来生成语义图或知识图[98]，[99]。 最近，已经提出了几种通用方法。 一些工作将生成过程作为形成结点和边的替代因素[64]，[65]，而其他工作则采用生成对抗训练[66]，[67]。 此类别中的方法或者将GCN用作构建块，或者使用不同的体系结构。

5.3.1 GCN Based Graph Generative Networks

• Molecular Generative Adversarial Networks (MolGAN)：
• Deep Generative Models of Graphs (DGMG)：

5.3.2 Miscellaneous Graph Generative Networks

• GraphRNN：
• NetGAN：

5.3.3 总结

评估生成的图仍然是一个难题。与可以由人类专家直接评估的合成图像或音频不同，生成的图的质量很难通过视觉检查。 MolGAN和DGMG利用外部知识来评估生成的分子图的有效性。 GraphRNN和NetGAN通过图统计信息（例如节点度）评估生成的图形。 DGMG和GraphRNN依次生成节点和边，而MolGAN和NetGAN联合生成节点和边。根据[68]，前一种方法的缺点是当图变大时，对长序列建模是不现实的。后一种方法的挑战在于，图形的全局属性难以控制。最近的一种方法[68]采用变分自动编码器通过提出邻接矩阵，施加惩罚项来解决有效性约束来生成图。但是，由于具有n个节点的图的输出空间为n 2，因此这些方法都无法扩展到大图。

5.4 Graph Spatial-Temporal Networks

图时空网络同时捕获时空图的时空相关性。时空图具有全局图结构，每个节点的输入随时间变化。 例如，在交通网络中，作为节点的每个传感器连续记录某条道路的交通速度，其中交通网络的边缘由传感器对之间的距离确定。 图时空网络的目标可以是预测未来的节点值或标签，或预测时空图标签。 最近的研究已经探索了单独使用GCN [72]，将GCN与RNN [70]或CNN [71]结合使用，以及为图结构量身定制的循环架构[73]。 在下面，我们介绍这些方法。

5.4.1 GCN Based Graph Spatial-Temporal Networks

• Diffusion Convolutional Recurrent Neural Network(DCRNN)：
• CNN-GCN：
• Spatial Temporal GCN (ST-GCN)：

5.4.2 Miscellaneous Variants

• Structural-RNN：

5.4.3 总结

DCRNN的优点是由于循环网络架构的缘故，它能够处理长期依赖性。 尽管比DCRNN更简单，但由于快速实施一维CNN，CNN-GCN可以更有效地处理时空图。 ST-GCN将时间流视为图的边缘，从而导致邻接矩阵的大小平方增长。 一方面，这增加了图卷积层的计算成本。 另一方面，为了捕获长期依赖关系，图卷积层必须堆叠多次。 结构化RNN通过在同一语义组内共享同一RNN来提高模型效率。 但是，Structure-RNN需要人类先验知识来拆分语义组。

6 Applications

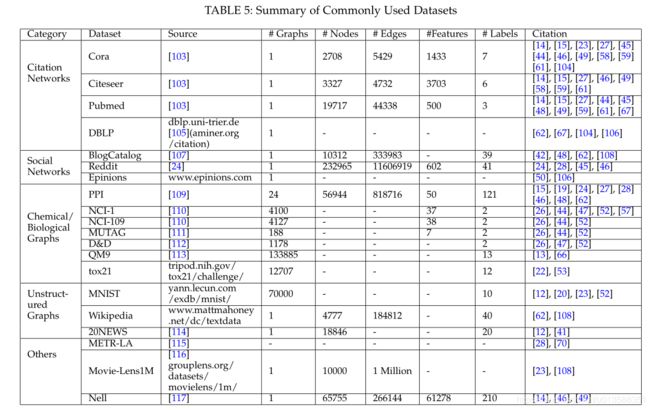
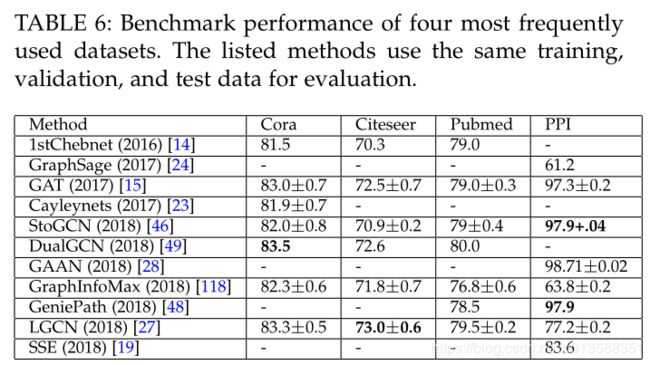
图神经网络具有广泛的应用。 在本节中，我们首先总结文献中经常使用的基准数据集。 然后，我们在四个常用数据集上报告基准性能，并列出图神经网络的可用开源实现。 最后，我们提供了图神经网络在各个领域中的实际应用。

6.1 Datasets

6.2 Benchmarks

6.3 Practical Applications

图神经网络在不同的任务和领域中具有广泛的应用。 尽管GNN的每个类别都有专门的常规任务，包括节点分类，节点表示学习，图分类，图生成和时空预测，但GNN还可应用于节点聚类，链接预测[119]和图分类 [120]。 在本节中，我们主要根据它们所属的一般领域介绍实际应用。

Computer Vision

Recommender Systems

Traffic

Chemistry

其他

GNNs在程序验证[18]、程序推理[139]、社会影响预测[140]、对抗攻击预防[141]、电子健康记录建模[142]、[143]、事件检测[144]、组合优化[145]等问题上的应用也有了初步的探索。

7 Future Directions

尽管图神经网络已经证明了其在学习图数据中的能力，但是由于图的复杂性，仍然存在挑战。 在本节中，我们提供了图神经网络的四个未来方向。

Go Deep

深度学习的成功在于深度神经体系结构。 例如，在图像分类中，名为ResNet [146]的杰出模型具有152层。 然而，关于图形，实验研究表明，随着层数的增加，模型的性能会急剧下降[147]。 根据[147]，这是由于图卷积的影响，因为它实际上将相邻节点的表示推向彼此更近的位置，因此，从理论上讲，在无限次卷积的情况下，所有节点表示都将收敛到一个点 。 这就提出了一个问题，即深度学习是否仍然是学习图结构数据的好策略。

Receptive Field

节点的感受野是指包括中心节点及其邻居的一组节点。 节点的邻居数遵循幂律分布。 一些节点可能只有一个邻居，而其他节点可能邻居多达数千个。 尽管已经采用了采样策略[24]，[26]，[27]，但是如何选择节点的代表性感受野仍有待探索。

Scalability

对于大型图，大多数图神经网络不能很好地缩放。 这样做的主要原因是，当堆叠图卷积的多层时，节点的最终状态涉及其大量邻居隐藏状态，从而导致反向传播的高度复杂性。 虽然几种方法试图通过快速采样[45]，[46]和子图训练[24]，[27]来提高其模型效率，但它们仍不足以扩展以处理具有大图的深度架构。

Dynamics and Heterogeneity

当前的大多数图神经网络都处理静态同构图。 一方面，假定图结构是固定的。 另一方面，假定图中的节点和边来自单个来源。 但是，这两个假设在许多情况下都不现实。 在社交网络中，新人可以随时进入网络，而现有人也可以退出网络。 在推荐系统中，产品可能具有不同的类型，其中产品的输入可能具有不同的形式，例如文本或图像。 因此，应开发新的方法来处理动态和异构图结构。

8 Conclusion

在这项调查中，我们对图神经网络进行了全面的概述。 我们提供了一个分类法，将图神经网络分为五类：图卷积网络，图注意力网络，图自动编码器和图生成网络。 我们对类别内或类别间的方法进行了全面的回顾，比较和总结。 然后，我们介绍图神经网络的广泛应用。 总结了图神经网络的数据集，开源代码和基准。 最后，我们提出了图神经网络的四个未来方向。