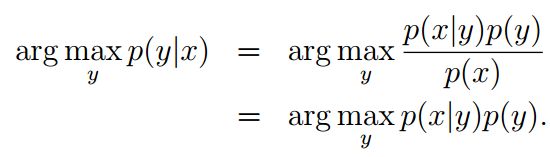《机器学习》(Machine Learning)——Andrew Ng 斯坦福大学公开课学习笔记(三)
第5集 生成学习算法
(一)生成学习模型:
例如:恶性和良性癌症的问题,分别对样本中恶性癌症和良性癌症的特征分别建模,当有新的样本需要判定时,看它是和哪个模型更像,进而预测该样本是良性还是恶性
学习p(x|y),p(y)(叫做class prior),通过贝叶斯推理后验概率:
因为p(x) = p(x|y = 1)p(y = 1) + p(x|y =0)p(y = 0)可以通过p(x|y)和p(y)表达,所以不用计算分母:
(二)判别学习算法:
直接学习 p(y|x),例如 逻辑回归直接学习输入空间到输出的映射关系
举例生成学习算法一:GDA(Gaussian discriminant analysis)
用高斯分布拟合两类样本的分布,当有新的样本需要判断时,通过贝叶斯计算后验概率,哪个更大,推理是哪一类
假设数据的分布:
y ∼ Bernoulli(φ)
x|y = 0 ∼ N (µ0, Σ)
x|y = 1 ∼ N (µ1, Σ)
最大似然求解参数:(似然的含义就是这些参数拟合的分布,训练集中的样本数据出现的概率最大,也就是说拟合的分布符合样本的分布)
GDA与逻辑回归的比较:如果样本实际(或近似)服从高斯分布,GDA假设样本符合高斯分布,分类效果会更好(原因是应用了数据的分布,使用了数据更多的信息)。但是如果分布不符合高斯分布,或者事先不知道数据的分布,逻辑回归更鲁棒。
举例生成学习算法二:Naive Bayes(垃圾邮件过滤)
Dictionary中包含m个词汇,指定x中x_i中的值(出现为1,否则为0)表示邮件内容,x的维度为字典中词汇的个数
要建模p(x|y),需要一个强假设,即Naive Bayes(NB)assumption,得到的结果即Naive Bayes classifier
条件独立假设:当邮件是垃圾邮件时,x_i出现的概率与x_j是否出现无关
即 p(x_2087|y) = p(x_2087|y, x_39831)(不等于说p(x_2087) = p(x_2087|x_39831)
对于两变量用 贝努力分布,多变量用多项式分布,对于连续变量可以离散化成set
Laplace smoothing:用于解决模型中没有学习到的word产生的概率为0的问题,分子分母加上一定数值
x1 = 1 (“a” is the first word in the dictionary)