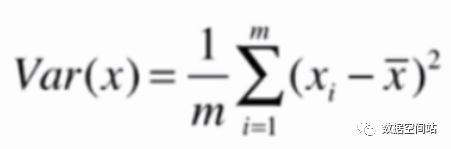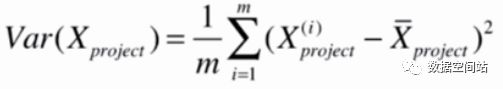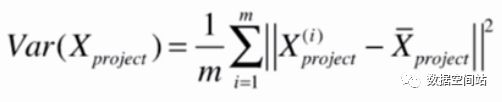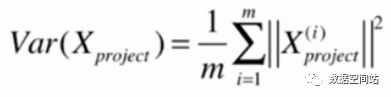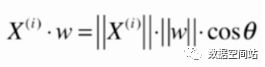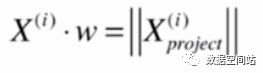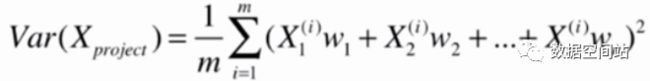机器学习入门系列之PCA降维

目录

 

前言

PCA降维原理

PCA如何降维

Sklearn实现

总结

---

前言

今天来说说机器学习中一个比较重要的概念——主成分分析(Principal Component Analysis)，简称PCA。根据字面意思强行解释一波，就是对主要的成分分析。专业一点就是：在减少样本维数的同时尽可能的保留原样本的信息，仅保留样本中所存在的主要特性，从而可以大大节省空间和数据量。

 

降维的好处：

1. 提升效率。我们往往面临成百上千的特征，如果对全部特征都处理，导致训练预测等处理特别慢

2. 不遗漏任何一个特征。以前特征数量过多时，会采用丢弃的策略，使用PCA可以将所有的特征映射到固定的数量维度上。

3. 将高维度的特征映射到低维度，便于理解以及可视化。

 

PCA降维原理

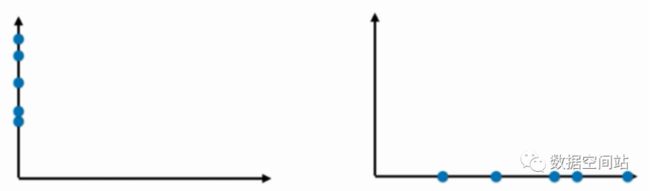
比如，我们有两个特征，如下图

 

现在需要对两个特征进行降维，降到一个维度。我们会想到可以将特征分别映射到X轴或Y轴，如下：

此时我们发现右边的降维效果似乎是更好一点，因为点和点之间的距离保持了原来的分布，更具有区分度。

但是如果这样降维，我们就会损失某个特征，而且有时候还不能最大程度的保持原分布。所以试想，在点之间是否可以找出一条直线，使得点映射到线上之后，可以最大的保持之前的分布与间距？

 

PCA如何降维

如何找一条直线，向量W=(W1，W2)，使得特征1和特征2映射到该直线后，样本点之间的间距是最大的？

掐指一算，此乃最优解问题。我们在前面讲了梯度下降法可以找到一个目标函数的最小值，同理我们只需要找到一个表示样本间距的目标函数，然后使用梯度上升法求得最大值即可。

在统计学中，一般用方差来定义样本的间距，方差公式如下：

对应的，样本如果有多个特征，X和均值X都为向量，那么公式就变为：

 

此时X都为矩阵，所以括号内部为向量，其实就是两个向量相减求模，所以可以写成以下公式：

此时就要进行PCA第一步，demean，即均值归零。所以原公式可以变为：

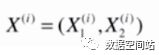如图，上面的线是我们要找的方向，下方的点是第i行的样本点，映射到w上，即对w做垂线，交点为。我们要求解的就是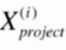的模的平方，即蓝色线的平方。

将向量映射到另一个向量上，求长度，其实就是向量的点乘。

由于向量w是方向向量，所以模为1

其实在直角三角形中， 就是。

所以就有

此时方差的公式可以变为

如果是n维数据，那么就有以下公式。

此时，我们就需要对以上函数求得最大值，可以利用梯度上升法/数学解法进行求取最优解，此处就不介绍了，可参考饼干大神的数据降维2：PCA算法的实现及使用

 

Sklearn实现

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
plt.scatter(X[:,0],X[:,1])
plt.show()

 

from sklearn.decomposition import PCA
#初始化实例对象，传入主成分个数，即降维后的维数
pca = PCA(n_components=1)
pca.fit(X)
# 对样本X进行降维
X_reduction = pca.transform(X)
X_reduction.shape
#OUT:(100,1) 可以看出X_reduction只有一个特征了。

​​​​​

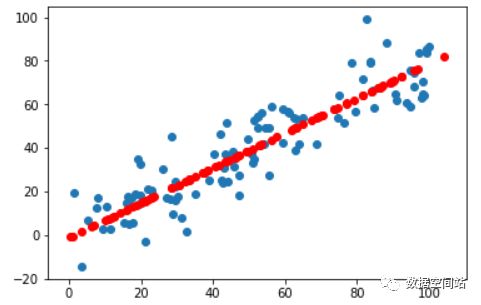
我们可以叠加到一张图上进行更清晰的查看

#对降维后的数据进行恢复成高维数据，但已经不是最原始的数据
X_restore = pca.inverse_transform(X_reduction)
plt.scatter(X[:,0],X[:,1])
plt.scatter(X_restore[:,0],X_restore[:,1],color='r')

 

 

总结

上面只是使用PCA进行简单数据的降维操作，PCA可以对更高维的数据进行特征抽取，使得算法更加精准，效率更高。

PCA对高维数据进行降维处理后，可以对降维后的数据再次进行恢复操作，使得转换到高维数据，但此时的高维数据已经不是最原始的数据了，而是经过PCA优化过后的数据（已经经过了demean处理），所以PCA往往也用来做降噪，人脸识别等等，后续会结合实际案例运用PCA大法，不要走开喔~

更多精彩：

机器学习入门系列之KNN

机器学习入门系列之线性回归

机器学习入门系列之评价模型的好坏

机器学习入门系列之特征处理

机器学习入门系列之梯度下降