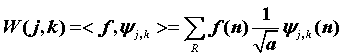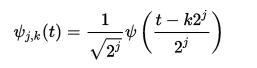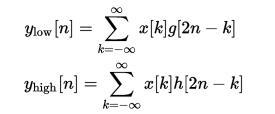图像压缩——小波变换（Wavelet Transform）从连续小波变换谈到离散小波变换

为什么会出现小波变换

窗口傅立叶变换（短时傅立叶变换）虽然可以部分定位时间，但由于窗口大小是固定的，只适用于频率波动小的平稳信号，不适用于频率波动大的非平稳信号。而小波变换可以根据频率的高低自动调节窗口大小，是一种自适应的时频分析方法，可以进行多分辨率分析。

从连续小波变换说起

连续小波变换（Continuous Wavelet Transform，CWT）的定义如下：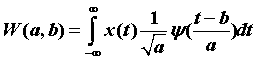

这里有两个变量——a，b，它们分别控制小波的两个变换。

scaling（或者叫dilation，延展）：stretching and shrinking the signal in time，完全由a控制，可以改变小波变换的中心频率（ center frequency）

设母小波的中心频率为Fc，那么子小波等效的信号频率（pseudo-frequency，伪频率）为：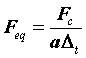
 （Fc是尺度为1的小波中心频率，a是尺度，delta t是采样间隔）或者写成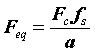（fs是采样频率）

在matlab中cwt将信号的采样频率归一化为1了.

可见，等效频率和尺度成反比关系。

中心频率指的是对小波进行傅立叶变换，最小的那个频率就是这个小波的频率，这个频率最能代表小波中间部分的频率和小波的能量。 the center frequency-based approximation captures the main wavelet oscillations. The center frequency is a convenient and simple characterization of the dominant frequency of the wavelet.

小波在时域上还是衰减的，且积分面积为0！

小波的中心频率和带宽 的计算公式如下：

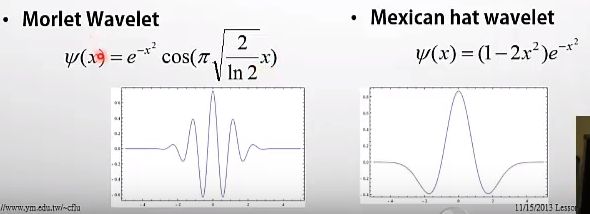
以Morlet wavelet为例，我们可以得到一些重要的结论：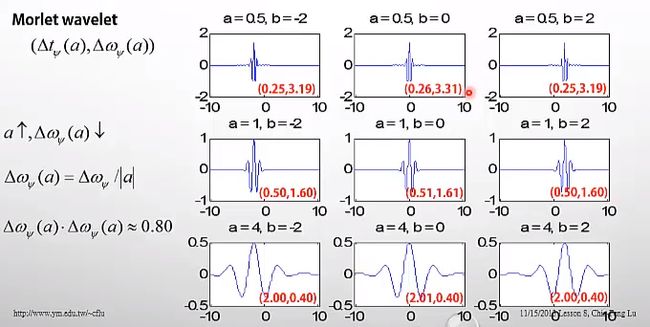

1.横着看，b不影响小波频率

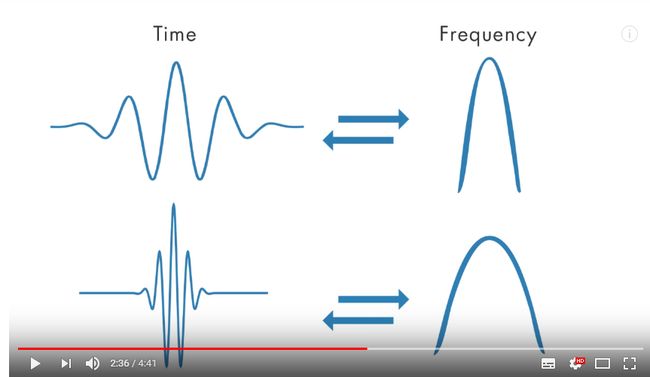
2.竖着看，a=1是基小波，当a<1时，时域压缩，带宽增大，频率增大；当a>1时，时域伸展，带宽减小，频率减小。

事实上，带宽只与a有关，而且时间宽度*频率宽度是一个常数。尺度越大，越低频，时间分辨率越高，频率分辨率越低；尺度越小，越高频，时间分辨率越低，频率分辨率越高。这一特性非常重要：

注：小波作用在信号上，具有带通特性：

shifting(或者叫translation，平移)：delaying or advancing the onset of the wavelet along the length of the signal，完全由b控制，控制小波基在时间轴上沿着信号滑动

举个例子：

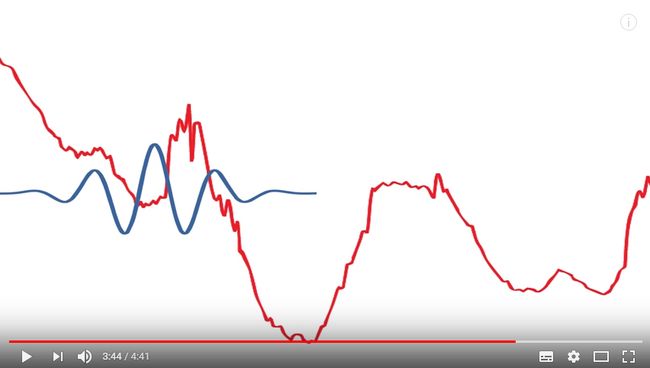
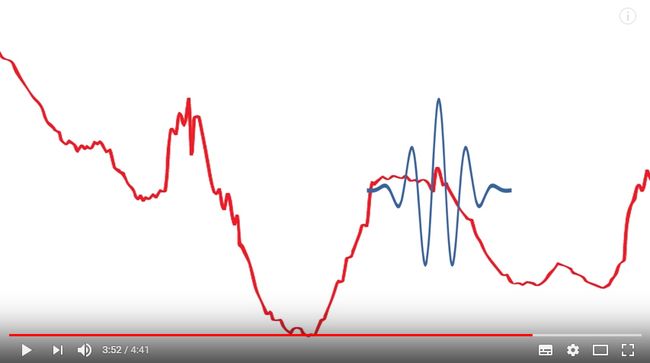
用小波刻画下面这个时间信号：

a stretched wavelet help capture the solely varying changes:

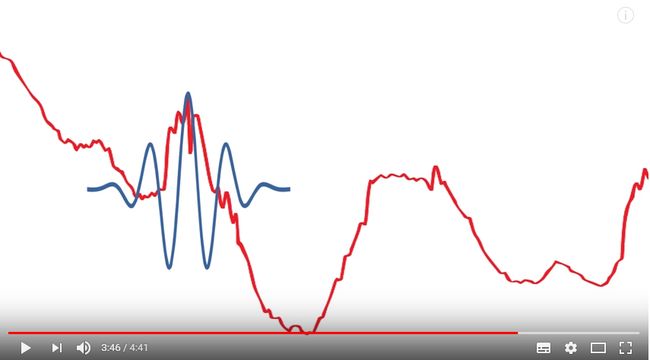
a compressed wavelet help capture the abrupt changes:

我们可以调整小波尺度构建出任意频率的子小波！！

连续小波变换的主要应用如下：time frequency analysis and filtering of time localized frequency components

常用的小波有：Morse Wavelets、Bump Wavelets、Analytic Morlet Wavelet

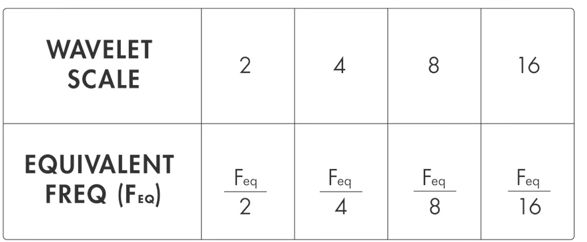
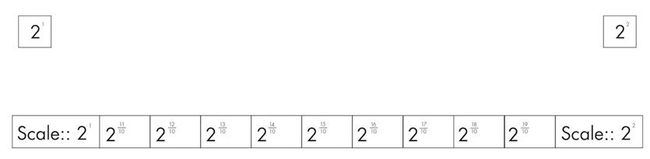
在实际应用时，将尺度以2为基底采样：

一般每一组的尺度个数选择：10 、12、16、32

将不同尺度的小波沿着信号移动，与信号比较得到一系列coefficients。例如1000 samples X 20 scales = 20,000 coefficients，以此刻画随时间振荡的信号

回到离散小波变换

离散小波变换（Discrete Wavelet Transform，DWT）定义如下，对连续小波的尺度和平移参数采样，一般是以2为底进行采样：

，

主要应用有：denoising and compression of signals and images 

由于内积运算太复杂，所以试图去找快速算法。

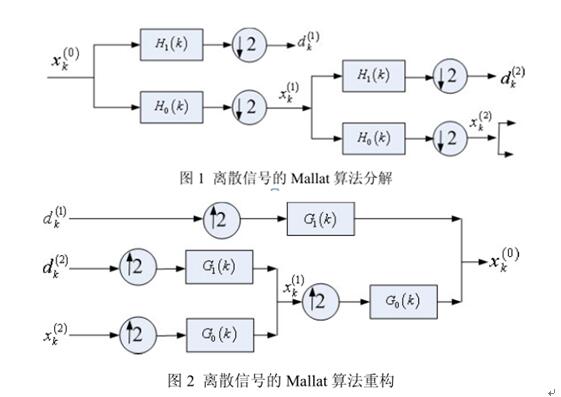
第一代小波：Mallat分解 1987

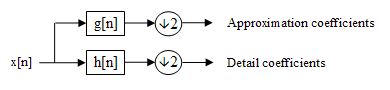
采用低通滤波器h(n)和高通滤波器g(n)，在行方向对图像滤波，并进行下2 采样；再在列方向滤波并进行下2 采样，可以进一步对低频部分进行多级小波金字塔分解。

First the samples are passed through a low pass filter with impulse response  g resulting in a convolution of the two.The signal is also decomposed simultaneously using a high-pass filter h. The outputs giving the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter.(正交镜像)

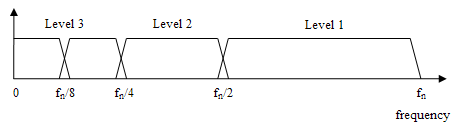
多次进行低通，高通滤波及将采样，可以得到如下滤波器组：

下面是3级变换后得到的4个输出的频率范围示意图：

分解后的序列是原序列与滤波器序列的卷积再进行隔点抽取而来。即分解抽取的结果长度为(srcLen+filterLen-1)/2。

分解与重构：

分解和重构滤波器的关系：

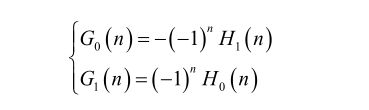
计算时边缘是要补0的，有如下方法：
1）零值填补
0 , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen -1
0 , srcLen -1< n≤srcLen+filterLen -2
举例说明：以“1 2 3 4 5 6 7 8”这个长度为8的信号为例，当滤波器的长度为4时，其具体的拓延长度为6（单边为3）：0 0 0 （1 2 3 4 5 6 7 8）0 0 0

2）周期拓延：
f(n+ srcLen) , -(filterLen -1)≤ n< 0
f′(n)= f(n) , 0≤ n≤ srcLen -1
f(n -srcLen) , srcLen -1< n≤srcLen+filterLen -2
举例说明：以“1 2 3 4 5 6 7 8”这个长度为8的信号为例，当滤波器的长度为4时，其具体的拓延长度为6（单边为3）：6 7 8 （1 2 3 4 5 6 7 8）1 2 3

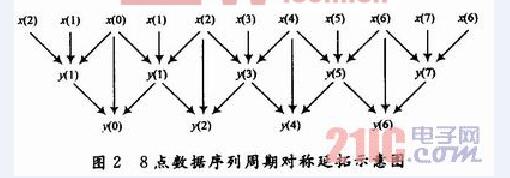
3）对称延拓（重点）
f(-n -1) , -(filterLen-1)≤ n< 0
f′(n)= f(n) , 0≤ n≤srcLen-1
f(2srcLen -n -1) , srcLen-1< n≤ srcLen+ filterLen-2
举例说明：以“1 2 3 4 5 6 7 8”这个长度为8的信号为例，当滤波器的长度为4时，其具体的拓延长度为6（单边为3）：3 2 1 （1 2 3 4 5 6 7 8）8 7 6

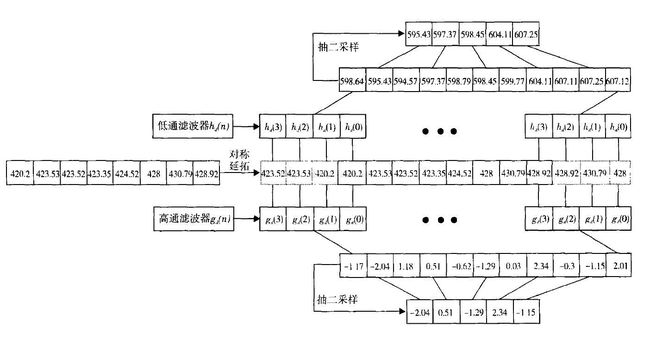
一个实例：

Mallat算法是基于卷积的，计算复杂度较高，存储空间要求较高。

第二代小波，提升格式（Sweldens和Daubechies等）1995

（1）分解。将输入信号s(i)分为2个较小的子集s(i-1)和d(i-1)。最简单的分解方法是按奇偶分为2 组，这种分裂所产生的小波称为懒小波（lazy wavelet）。
（2）预测。在基于原始数据相关性的基础上，用偶数序列s(i-1)的预测值P(s(i-1))去预测（或者内插）奇数序列d(i-1)，即将滤波器P对偶数信号作用以后作为奇数信号的预测值，奇数信号的实际值与预测值相减得到残差信号。实际中虽然不能从子集s(i-1)中准确地预测子集d(i-1)，但是P(s(i-1))有可能很接近d(i-1)，因此我们可以使用P(s(i-1))和d(i-1)的差值来代替原来的d(i-1)，这样产生的d(i-1)比原来的 d(i-1)包含更少的信息，于是得到d(i-1)=d(i-1)-P(s(i-1))，这里，已经可以用更小的子集s(i-1)和子集d(i-1)来代替原信号集s(i)。重复分解和预测过程，经过n步以后原信号集可用{s(n),d(n),s(n-1),d(n-2),.....,d(1)}来表示。
（3）更新。为 了使原始信号集的某些全局特性在其子集s(i-1)中继续保持，使得它保持原图的某一标量特性Q(x)（如均值、消失矩等不变），即有Q(s(i-1))=Q(s(i))。可能利用已经计算的小波子集d(i-1)对s(i-1)进行更新，从而使得后者保持特性Q(x)，即要构造一个算子U去更新 s(i-1)。定义如下：
s(i-1)=s(i-1)+U(d(i-1))
从上述分析可以知道，提升方法可以实现原位运算，即该方法不需要除了前级提升步骤的输出之外的数据，这样在每个点都可以运用新的数据流替换旧的数据流。

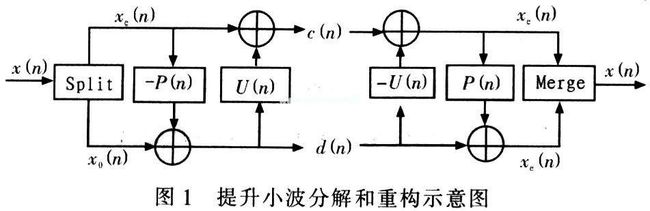
优点：速度是mallat分解的两倍，可以实现原位运算（同址运算，不需要额外的存储单元），可以实现整数小波变换，实现无损压缩。

JP2K里的小波压缩

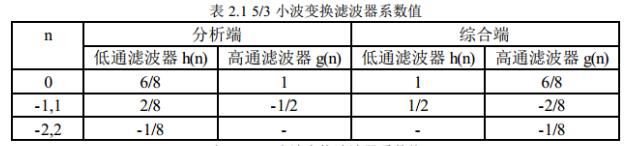
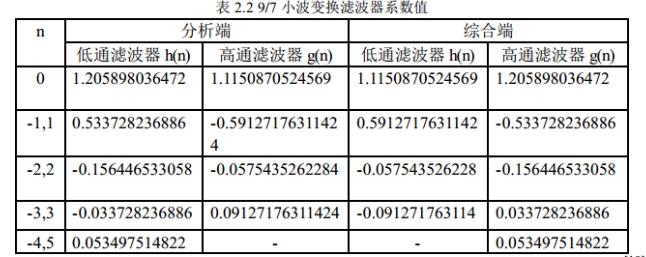
Le Gall 5/3小波变换，用于无损压缩

分解是将数据分为偶数序列和奇数序列2个部分，预测是用分解的偶数序列预测奇数序列，得到的预测误差为变换的高频分量，更新是由预测误差来更新偶数序列，得到变换的低频分量。

Daubechies 9/7小波变换，用于有损压缩

双正交小波基，具有线性相位，消失矩较大，能量集中性好等特性，在图像处理领域有广泛的应用。图像经过9 /7小波分解后的低频部分分辨率高，高频部分细节突出。

9 /7小波增加了一个预测和更新环节，可以防止图像重建误差的扩大，提高系统稳定性，同时也保留了原位计算的特性，运算所需内存少，变换速度快。

5/3的分解与重构matlab实现：5/3分解与重构

Verilog代码通用性不强，就不上了。

附上一个经典的小波教程(含中文翻译)：WaveletTutorial原文及其翻译