n |= n >>> 1——JDK10的HashMap原理 tableSizeFor(initialCapacity)方法

前言

今天我大儿子在我们房子罚款群里问了一个问题，问题如下：
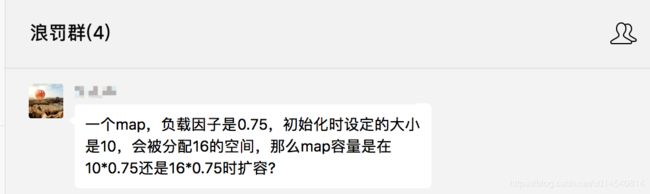这个问题的答案是16，hashmap具体的知识，自行百度，知道了hashmap的大概知识之后再看回来我下面说的。

为什么是16呢，因为在hashmap在扩容的时候会对threshold进行判断，size大于等于threshold就扩容。这个threshold就是2的次方数，2的次方数就是2的几次方的意思。threshold取得值，是你设定大小的下一个2的次方数。10的下一个2的次方数是16，所以答案是16。

这个答案是通过阅读源码得到的。是对的，不信你往下看。

源码在哪里？我们找一下。
这是map的put方法所调用的putval：我们只看最后的部分就好。

/**
     * Implements Map.put and related methods
     *
     * @param hash hash for key
     * @param key the key
     * @param value the value to put
     * @param onlyIfAbsent if true, don't change existing value
     * @param evict if false, the table is in creation mode.
     * @return previous value, or null if none
     */
    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node[] tab; Node p; int n, i;
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
            Node e; K k;
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            else if (p instanceof TreeNode)
                e = ((TreeNode)p).putTreeVal(this, tab, hash, key, value);
            else {
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

最后的关键部分：

if (++size > threshold)
            resize();

resize就是扩容方法。
那么threshold从哪里来？狗子方法中（打错了，应该是构造方法，哈哈哈，不过这样挺有意思，哈哈哈哈哈哈）最后一行进行了赋值：

/**
     * Constructs an empty HashMap with the specified initial
     * capacity and load factor.
     *
     * @param  initialCapacity the initial capacity
     * @param  loadFactor      the load factor
     * @throws IllegalArgumentException if the initial capacity is negative
     *         or the load factor is nonpositive
     */
    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                               initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                               loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }

构造方法中最后一行就是：
this.threshold = tableSizeFor(initialCapacity);

那么这个this.threshold = tableSizeFor(initialCapacity);是怎么回事呢？我们看他的源码：

/**
     * Returns a power of two size for the given target capacity.
     */
    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

这就是我们要找的部分了。

看到了这些代码，我一下就回想起了大学时，教我们逻辑电路那个老师了，什么短路与，运算或，与或非，异或，左移右移，这堆烂码七糟的东西。

我忘了这老师叫啥了，名字好像是仄仄平或者平仄平。

他的形象一直能想起来，中年，短粗胖，喝酒。哇啦哇啦的。

后来问了同学，知道了，他叫仄平仄。。。和我记得完全不一样。

那这段代码是什么意思呢，看到的时候我很懵，后来仔细看，照着算一下，也就明白了。

关键代码的问题解析

|

首先，什么是|。就是二进制运算时，有1就是1。
1|0=1，1|1=1，0|0=0。

>>>

右移几位。直接往右移就完了，0补位，很简单。
111>>>1=011。
111>>>2=001。

开始计算

这段代码到底咋回事？

		int n = cap - 1;
		n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;

他的意义就是找到比输入大的，并且与输入相邻的2的次方数。
比如输入3，输出4。输入5、6、7，输出8。

我们只要跟着算一下就会明白了。下面开始计算。以输入10为例。你也可以随便选择一个数，按照下面步骤进行。

比如输入10，10-1=9，9化成二进制就是：1001。
然后开始这步：

n |= n >>> 1;

此时n=1001,n先右移1位，变成0100。
然后0100再与之前的n做与运算，也就是0100|1001=1101。
此时n=1101。

然后是：

n |= n >>> 2;

1101>>>2=0011
0011|1101=1111
此时n=1111。

然后是：

 n |= n >>> 4;

聪明的人已经知道了，以后的结果都是1111，不信给你算。
1111>>>4=0000
0000|1111=1111
此时n=1111。

然后是

 n |= n >>> 8;

1111>>>8=0000 0000
0000 0000|1111也就是0000 0000|0000 1111 = 0000 1111
0000 1111也就是1111。
此时n=1111。

移16就不用算了，你得多笨。

这时候发现了啊，一直右移，做与运算，最后就变成了全是1的。然后再看tableSizeFor的代码最后一行，最后要得到n+1。

return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;

这段代码先是判断n是否小于0，这个防御判断就不用管了。大于0的时候，判断n和MAXIMUM_CAPACITY的大小，取值MAXIMUM_CAPACITY或者n+1。

这里可以这么理解：
n >= MAXIMUM_CAPACITY 可以写成n + 1 > MAXIMUM_CAPACITY
也就是：
(n + 1 > MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
然后就理解成，n+1和MAXIMUM_CAPACITY谁大就取谁。

我们输入的10，最后得出1111，1111+1之后是几？是10000，16，也就是2的4次方。

几个问题：

为什么取的是n+1呢？计算的结果都是1的，我们加了1之后就会进一位并且变成1000…000。变成2的次方数。

我们是怎么保证输出一定大于等于输入的呢？
1）我们输入的数，转为二进制之后，最大的情况也不过是，11111…111这样的，如果是这样，那么输出=输入。
2）如果我们的输入不是1…11111…111这种情况，也就是说，此时不是最大值，此时 必有的位为0，经过计算之后，位0的位变为1，必比变换之前大。

那有人说了，为什么这里我输入的数字，是位数很多的呢？位数多到，上述的最后一步>>>16都不能包括我所有的位数。那不是上述操作移完了之后还会有0存在吗，也就是得出的数不是2的次方数了。

不好意思，输入类型是int型。int型最大值是2的31次方。

而上述计算中。>>>1相当于除以2的1次方。
然后>>>2是除以2的2次方。
然后>>>4——2的4次方。
然后>>>8——2的8次方。加起来是15次方。
最后>>>16——2的16次方，加起来就是一共运算了2的31次方的数。所以你输入的int型，都可以移动的到。

你的担心不存在啊。

结论

多算几个数我们会发现规律：
设输入x，x的二进制数共有k位。
经计算之后，得出数y，y共有k+1位。
并且：y为大于x的，2的次方数的最小值。

我乍看有所疑惑的这段代码，原来就是这么回事。