坐标系变换

坐标系变换

Think an invertible matrix as a coordinate.

坐标系变换，例如，现在有一个点P，在A坐标系中的坐标为 (x,y) ，如何求出点P在其他坐标系下的坐标呢？比如，我们想知道P点在B坐标系中的坐标？

做个类比，如果两个讲不同母语的人想要交流，怎么办？这时，如果有一种世界通用语言就好了，例如汉语。这样，当说英语的人向说法语的人问候“你好”的时候，他知道要查字典先把英文 “hello”转换成中文“你好”，然后，说法语的人就可以将“你好”转换成法文“Bonjour”。

这里有两个过程：

• hello → 你好
• 你好 → Bonjour

这两个过程中有一个关键点：

你好 —汉语

是的，世界通用语言，我们的汉语，就是key point， 她在不同语系中充当了桥梁的角色。

回到坐标系的话题，使用不同的坐标系就像使用不同的语言，各说各话，相互之间是无法被理解的。如果想要被理解，那就的使用大家都认同的方式交流。这时候，如果引入一个参考坐标系，世界就和平了：

我们可以将P点的坐标先转化为一个参考坐标，然后再从参考坐标转换到B坐标系中的坐标。

• A → Global
• Global → B

现在，我们的问题变成了求某个坐标系X与参考坐标系Global之间的转换方法：

X ↔ Global

不考虑平移

如果考虑不同的坐标系共原点，就像下面这样：

选择坐标系A作为参考坐标系，如何表述：

B ↔ A

答案是：矩阵变换

矩阵变换就像词典翻译一样，将一个坐标系下的点转换成另一个坐标系中的点。

矩阵与线性变换中提到了在同一个坐标系中矩阵变换的作用，例如，将一个向量进行旋转。现在，矩阵变换被不可思议的用作了坐标系变换的工具。变换还是同样的变换，只是站在了不用的角度看待问题：

• 矩阵变换之于同一个坐标系，可以理解为坐标系不变，点的位置改变。
• 矩阵变换之于不同坐标系，可以理解为点的绝对位置不变，坐标系改变。

其实在矩阵与线性变换拓展一节中，我提到了一种转换关系，这里，我给出上图的对应表述：

(1) [x′y′] = B[xy] ⇒ [xy] = B−1[x′y′] ， B = [b1→b2→] ， 且 b1→，b2→ 是坐标系B的基向量

其中，矩阵 B 的各个列向量分别对应B坐标系的各个基向量， [xy] 是向量 OP→ 或者说点P在B坐标系的表示， [x′y′] 则是向量 OP→ 或者点P在A坐标系中的表示。求出矩阵 B ，我们就有了翻译用的字典。

这一切，在于矩阵 B 的各个列向量，在于B坐标系的基向量。

(1) 的转换关系之所以成立，是因为矩阵 B 的各个列向量是B坐标系的基向量，他们都是坐标系A中的向量。更明确的说，矩阵 B 的列向量由坐标系A的基向量通过一个线性变换得到，这个线性变换完全可以用矩阵 B 表示，详见矩阵与线性变换。

上图对应的矩阵B的两个列向量分别为 b1→ = [25√/55√/5] ， b2→ = [−5√/525√/5] 。

其实A、B可以是任何坐标系，式(1)仍然成立，只要满足：

• 坐标系A和坐标系B原点均为(0,0)
• 矩阵 B 的各个列向量分别对应B坐标系的各个基向量
• 矩阵 B 的各个列向量都是坐标系A中的向量

坐标系B的基向量是坐标系A的基向量的一个线性变换 ，这个线性变换可以用矩阵 B 表示( T(x⃗ )=Bx⃗  )，确定坐标系B的基向量在A坐标系中的表示的过程叫做B坐标系的定位(landed)。将B坐标系的基向量定位在A坐标系中确定了一种关系，我们暂且把这种关系称为追溯关系，把A坐标系称为B坐标系的上游坐标系。反过来，如果把坐标系A的基向量定位在B坐标系中，那么B坐标系就成了A坐标系的上游坐标系。

下面，用图说话：

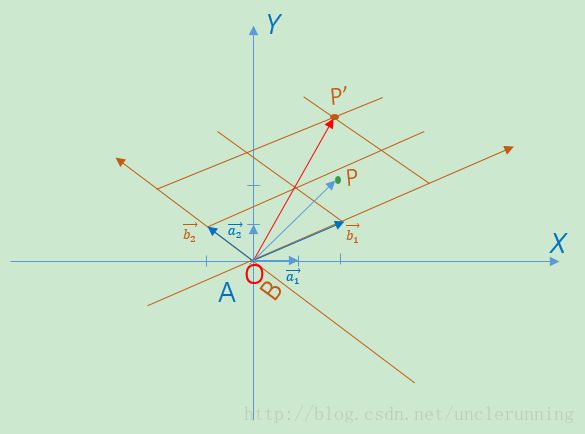
以图中的两个向量 b1→,b2→ 为基确定一个坐标系B，显然，在B坐标系中 b1B→=[10],b2B→=[01] ， 接下来，将 b1→,b2→ 定位到A坐标中，得到 b1A→=[21],b2A→=[−11] 。

∵ OP→ = 2 b1→ +2 b2→

∴ OP→ 在B坐标系中的表示为 [22] ，现在，将 OP→ 用A坐标系描叙：

OP→ = 2 b1→ +2 b2→ = 2b1A→+2b2A→ = [b1A→b2A→] [22] = [24]

现在，令矩阵 B = [b1A→b2A→] ，P点是用B坐标系表示的任意一点 (x,y) 。

于是 OP→ 在A坐标系中的表示 [x′y′] = B [xy] ，显然， B 是可逆的，于是就有了(1)式的结论。

虽然这里的讨论是基于二维的，但是，不难想象，这里得出的结论可以扩展到任意维度。

用一句话来阐述这个结论：

将B坐标系的基向量定位到A坐标系，然后将定位之后的基向量作为矩阵 B 的列向量，用矩阵 B 对B坐标系中的点P的坐标进行矩阵变换，将得到点P在A坐标系中的坐标。这个过程，就是从坐标系B到坐标系A的一个追溯过程。

加入平移

平移好像没什么好说的，不过就是在前面讨论的基础上引入一个偏移。

下面用图示说明：

上图引入了一个新的坐标系，取名为A’。将这个坐标系取名为A’是有原因的，因为他基本就是坐标系A的一个替身，他们之间除了坐标原点发生偏移之外，其他特征完全一致。

有了前面的基础，我们知道，将坐标系B中的坐标转换为坐标系A’中的坐标其实就是一个从B到A’的追溯过程。只要将坐标系B的基定位到A’坐标系中，以定位之后的基向量为列组成矩阵 B ，然后对坐标系中的坐标进行 B 矩阵转换就能得到其在A’坐标系中的坐标。反过来，求出矩阵 B 的逆，我们就能将A’坐标系中的坐标转化为B坐标系中的坐标。

也就是说，利用前面讨论的结论，我们能完成：

B↔A′

[x′y′] = B[xy] ⇒ [xy] = B−1[x′y′]

剩下的问题就是：

A′↔A

这个问题就是一个加减偏移量的问题，所以看图就一目了然了。

齐次坐标系与平移

引入齐次坐标的好处之一是可以使用矩阵表达平移：

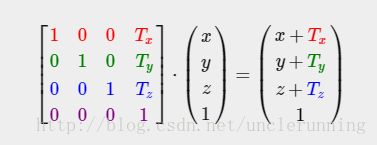
所以 A′↔A 之间的变换可以用这么一个矩阵变换来完成。

追溯过程

将坐标系B的基向量定位到坐标系A’中，得到向量 b1A′→,b2A′→ ，所以从坐标系B追溯到坐标系A’的矩阵 B = [b1A′→b2A′→] 。 A′→A 的平移矩阵 T 为 ⎡⎣⎢100010TxTy1⎤⎦⎥ 。

故，将坐标系B中的点 p(xB,yB) 追溯到坐标系A中可以用下面的矩阵变换表示：

1). 将坐标变换到坐标系A’：

[xA′yA′] = B [xByB]

2). 将坐标变换到坐标系A中：

[xAyA] = T [xA′yA′]

综合起来就是：

[xAyA] = T B [xByB]

反过来， A→A′ 的平移矩阵 T′ 为 ⎡⎣⎢100010−Tx−Ty1⎤⎦⎥ ，从坐标系A’追溯到坐标系B的矩阵 A′ = B−1

故，将坐标系A中的点 p(xA,yA) 追溯到坐标系中B中可以用下面的矩阵变换表示：

[xByB] = A′ T′ [xAyA] = (TB)−1 [xAyA]

矩阵变换：坐标系变换 or 位置变换

站在不同的角度看同一个矩阵变换 Bx⃗  ：

1). 位置变换：

A坐标系中：

向量 OP→=[22] ， 向量 b1→=[21] ， b2→=[−11] ， 令矩阵 B = [b1→b2→] ，则矩阵变换 Bx⃗  会将 OP→ 变到 OP′→ 。

2). 坐标系变换：

B坐标系中：

向量 OP′→=[22]

A坐标系中：

向量 b1→=[21] ， b2→=[−11] ， 令矩阵 B = [b1→b2→] ，则矩阵变换 Bx⃗  会将 OP′→ 从坐标系B变到坐标系A。

总结

于是，对任意坐标向量 x⃗  ，矩阵变换的组合 M1M22M3...Mn 作用于 x⃗  存在两种解释。

x′→ = M1M22M3...Mn x⃗  的两种解释：

1). 坐标系不变，位置变换：

将 M1M22M3...Mn 看作从右到左依次作用的矩阵变换。首先 Mn 变换， 将坐标向量 x⃗  变换到了 xn−1→ = Mn x⃗  ，接着是 Mn−1 变换，将坐标向量 xn−1→ 变换到了 xn−2→ = Mn−1 xn−1→ …。所有的中间结果都是同一个坐标系中的坐标向量，所有的变换都是针对同一个坐标系的变换。

2). 位置不变，坐标系变换：

将 M1M22M3...Mn 看作从左到右依次作用的矩阵变换。首先 M1 变换，将M1坐标系中的坐标向量 x1→ 转换为起始坐标系中的向量 x′→ ， x′→ = M1 x1→ ，然后是 M2 变换，将M2坐标系中的坐标向量 x2→ 转换成M1坐标系中的坐标向量 x1→ ， x1→ = M2 x2→ …最后是 Mn 变换，将Mn坐标系中的坐标向量 x⃗  转换成Mn-1坐标系中的坐标向量 xn−1→ ， xn−1→ = Mn x⃗  。所有的中间结果都是不同坐标系中的坐标向量，且坐标向量的绝对位置没有改变（想象该点被一个钉子钉住）。从Mn坐标系的坐标向量 x⃗  依次与 MnMn−1...M3M2M1 矩阵相乘最终转换到起始坐标系对应的坐标向量 x′→ 的过程就是一系列前面提到过的追溯过程。