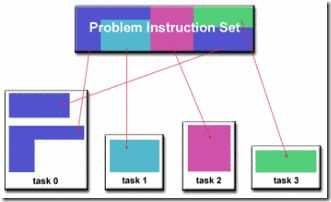
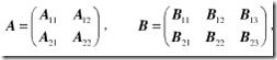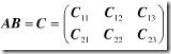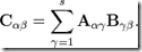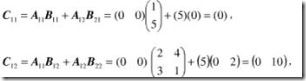并行编程中的设计模式
这篇文章是对这段时间学习并行编程中的设计模式的一个总结。有不当之处,希望得到大家的批评、指正。
首先,所谓“并行编程中的设计模式”(patterns in parallel programming)仍处于不断的被发现、发掘的阶段。当前已经有各路人马对这一领域进行了研究,但远远没有达到统一认识的高度。也没有一套业界普遍认同的体系或者描述。这就造成了当前这一领域的现状:从事研究的人有不同的背景,他们各自总结出的模式种类不尽相同。即使是同一个模式,不同的团队给它们取得名字也可能不一样。不过这并不妨碍我们对“并行编程中的设计模式”进行一定的了解,并在实际的软件开发工作中有所借鉴。
本文分两部分,第一部分会简单介绍这一领域的发展现状:首先是进行研究的主要团体及其代表人物,然后介绍一下他们各自总结的模式体系,最后着重介绍一下加州大学伯克利分校的体系,A pattern language for parallel programming。第二部分则从该体系中挑出八个常用的设计模式作稍微详细一点的介绍。每个设计模式都附有实际的应用例子来帮助理解。我始终相信,通过例子的学习是最容易理解的一种方式。
1. 并行编程模式的发展现状
在这一领域比较活跃的研究团体包括:
1. 加州大学伯克利分校。其代表人物是Kurt Keutzer教授,他曾是Synopsys公司的CTO。
2. Intel公司。代表人物是Tim Mattson,他是Intel的Principle Engineer和并行计算的布道师(evangelist),是“Patterns for Parallel Programming”一书的作者。
3. 伊利诺伊大学。代表人物是Ralph Johnson教授。他是著名的设计模式“Gang of Four”中的一员。
4. 其他团体:包括微软、麻省理工大学… 等等。
他们总结出的并行编程模式体系不尽相同,互相之间又有着紧密的联系。主要有:
1. 加州大学伯克利分校的 A Pattern Language for Parallel Programming ver2.0
2. 伊利诺伊大学的 Parallel Programming Patterns
3. Tim Mattson 的著作 Patterns for Parallel Programming
这其中,我最为喜欢加州大学伯克利分校的体系:
伯克利的研究人员认为,写出高质量并行软件的关键在于拥有好的软件设计:从软件的总体架构,一直到系统的底层实现。将这些“好的设计”以一种系统的方式描述出来,并在各个不同的软件项目当中重用是解决构建高质量并行软件问题的关键。这远比各种具体的编程模型以及其支撑环境来得重要。因为拥有了一个好的设计之后,我们可以很容易的在各种开发平台上编写源代码。
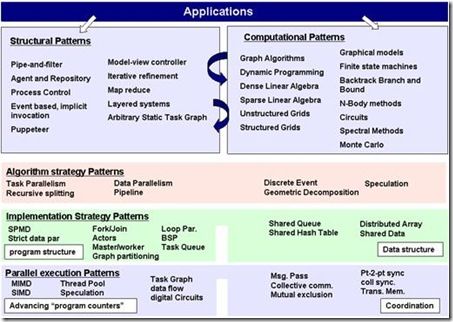
伯克利的模式体系包含了几个不同的层次,上自软件架构,下至程序指令执行的策略。最上面的两块分别是“架构模式”(Structural patterns) 和“计算模式”(Computational patterns)。这两块并不单单包括并行软件,也包括传统的串行软件模式。用我们常用来表达系统架构的线框图打比方,“架构模式”指的就是那些箭头和框框,它们表示的是程序总体的组织结构,以及各部分之间是怎么交互的。“计算模式”指的是框框里面的计算类型。例如,是基于图的算法,还是有限状态机,还是线性代数运算,等等。程序设计师通常需要在这两大类模式之间翻来覆去的进行选择。例如,我们可能先选择了一种架构模式,然后考虑使用某些合适的计算模式。但是选择的计算模式可能更适合于在另一种架构模式下运行,所以我们又得重新选择一种架构模式… …如此反复。上面这张图在“架构模式”和“计算模式”这两大块之间画了两个反复的箭头,表达的就是这个意思。
这张图下方的三大块就专指并行编程当中的模式了。它们包括“算法模式”(Algorithm strategy patterns),“实现模式”(Implementation strategy patterns)和“并行执行模式”(Parallel execution patterns)。顾名思义,“算法模式”指的是程序算法层面的模式。它们表达的是,为了解决某一类实际问题,怎么样在较高的算法层面实现并行。“实现模式”指的是我们在编写源代码的时候,利用什么样的一些程序控制结构和数据结构来实现并行。例如“parallel_for”,例如并行容器,等等。最后一个“并行执行模式”指的是为了在计算机中有效的执行一个并行程序,我们应该采取哪些方法。这包括指令的执行模式,例如是MIMD还是SIMD,也包括一些任务调度的策略。这三类模式是紧密联系在一起的。例如,为了解决一个问题,我们可能使用“recursive splitting”的算法模式。而为了实现这个算法,我们很有可能使用“fork-join”的实现模式。在执行层面,并行程序库则通常会用“thread pool”的并行执行模式来支持“fork-join”的运行。
由于我们在编写程序时,“并行执行模式”往往由编译器或并行程序库例如TBB的编写人员考虑,我们并不需要关心;“实现模式”和我们选择的具体并行运算平台有关(OpenMP, TBB,MPI,…,,等等),不同的平台有不同的API;“计算模式”则和具体的问题域联接紧密。而且,看上去伯克利所总结的“计算模式”大部分和高性能计算有关,普通的应用程序员并不熟悉。所以在本文,我将只挑选和并行计算密切相关的两个“架构模式”和六个常见的“算法模式”举例进行说明。
2. 八个常用的并行编程模式
2.1 Agent and Repository
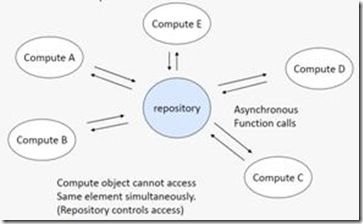
这是一个“架构模式”,它针对这样一类问题:我们有一组数据,它们会随机的被一些不同的对象进行修改。解决这一类问题的方案是,创建一个集中管理的数据仓库(data repository),然后定义一组自治的agent来操作这些数据,可能还有一个manager来对agent的操作进行协调,并保证数据仓库中数据的一致性。我们常见的源代码版本控制软件例如Perforce就是实现这种架构的典型代表:源代码都存放在一个统一的服务器中(或是一组服务器中,但对client而言是透明的),不同的程序员们使用各自的客户端对源代码文件进行读,写,加,删的操作。由Perforce负责保证源代码数据的一致性。
2.2 Map Reduce
Map Reduce这个名词原来是函数式编程里面的一个概念,但是自从Google于2004年推出同名的并行计算程序库后,提到这个名词大家大多想到的是Google的这个Framework。在这里,Map Reduce是一个“架构模式”的名称。当然,我们这里的Map Reduce指的就是类似Google Map Reduce工作原理的一类模式。
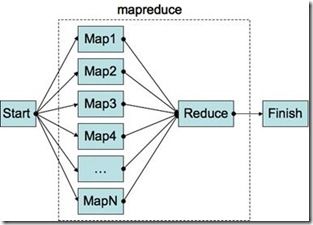
那么什么是Map Reduce的模式呢?用较为简单的语言描述,它指的是这样一类问题的解决方案:我们可以分两步来解决这类问题。第一步,使用一个串行的Mapper函数分别处理一组不同的数据,生成一个中间结果。第二步,将第一步的处理结果用一个Reducer函数进行处理(例如,归并操作),生成最后的结果。从使用Google的Map Reduce程序库的角度而言,作为应用程序员,我们只需提供一组输入数据,和两个普通的串行函数(Mapper和Reducer),Google的Map Reduce框架就会接管一切,保证输入数据有效的在一个分布式的计算机集群里面分配,然后Mapper和Reducer函数在其上有效的运行、处理,并最后汇总生成我们想要的处理结果。所有一切的细节,例如并行化、数据的分配、不同机器之间的计算误差,通通被隐藏在程序库内。
那么Map Reduce到底是什么样的一个过程呢?
我们讲过,使用Map Reduce,程序员必须提供一组输入数据,以及一个Mapper和一个Reducer函数。在这里,输入数据必须是一个按(input_key,input_value)方式组织的列表。
mapper函数的任务是处理输入列表中的某一个单元数据:mapper(input_key,input_value),并产生如下输出结果:
接下来,把对所有单元数据的处理结果按照intermediate_key归类:同样的intermediate_key放在一起,它们的intermediate_value简单的串接起来,得到:
Reducer函数的任务是对上述的中间结果进行处理:reducer(intermediate_key, intermediate_value_list),并产生如下最终输出结果:
我们会举两个例子说明这一过程。第一个例子是一个简单的统计单词出现次数的小程序。第二个例子是Google曾经怎样使用Map Reduce FrameWork来计算Page Rank。
第一个例子,假设我们要写一个小程序,来统计在几篇不同文章里所有出现过的单词各自总共出现的次数。我们应该怎么做呢?下面描述的利用Map Reduce的方法肯定不是大多数程序员第一感会想到的方法。但这种方法非常好的揭示了Map Reduce的基本思想。并且,这种方法很容易被扩展到处理上千万甚至是上亿的文件数据,并且能够在一个分布的计算机集群里面运行。这可不是传统的方法能够轻易做到的。
具体而言,假设我们有如下三个文本文件,a.txt, b.txt和c.txt:
对于输入数据而言,input_key就是文件名,input_value就是一个大的string,包含的是文件内容。所以我们的输入数据看上去会是这样的:
我们会写一个简单的串行的mapper(fileName, fileContent)函数。这个函数做的事情很简单,读入一个文本文件,把每一个遇到的单词当作一个新的intermediate_key,并赋其intermediate_value为1。将mapper函数处理文件a,我们会得到如下结果:
![]()
将所有三个文件的处理结果放在一起,我们得到:
然后将中间结果按intermediate_key归类:
最后,由reducer(intermediate_key, intermediate_value_list)对中间结果进行处理。它做的事也很简单,仅仅是把某intermediate_key对应的所有intermediate_value相加。我们于是得到最终结果:
第二个例子,怎样使用Map Reduce计算PageRank。什么是PageRank?可能大家都有所了解,这是Google用来量度一个网页的重要性的值。简单而言,有越多的其它网页链接到这个网页,这个网页的PageRank越高。链接到这个网页的网页PageRank越高,这个网页的PageRank也越高。假设我们一共有n个网页0, 1, …, n-1。对第j个网页我们给它赋一个PageRank值qj。所有的qj组合起来成为一个向量q = (q0,q1, …qn-1)。这个向量满足概率分布。即qj的值都在0和1之间,并且所有的qj加起来等于1。qj越大,网页的重要性越高。那么q是怎么计算出来的呢?答案是使用迭代的方法: ![]()
我们从一个初始的PageRank向量分布P开始,乘以一个n*n的矩阵M,得到一个新的PageRank向量。把新的PageRank向量继续乘以M得到下一步的PageRank… … 如此迭代有限步后,PageRank向量的值会趋于收敛,于是我们得到最终的PageRank。
这里需要回答两个问题:1. 如何确定初始的PageRank,即迭代的起点?答案是任意选择一个概率分布就可以,无论你选择什么初始值,都不影响其收敛到最终的结果。我们通常使用均匀概率分布,即![]() 。2. 如何定义M?这个问题稍显复杂,有兴趣的读者可以参见Michael Nielsen 的博文Using MapReduce to compute PageRank了解更详细的内容。在这里,我们将其简化的定义为一个描述网页间互相链接结构的超大矩阵。假设网络里有n个网页,那么我们这个矩阵就是一个n*n的方阵。矩阵的每一列代表一个网页对外的超链接情况。例如,我们定义#(j)为第j个网页对外的所有超链接的数量。那么对于矩阵M的第j列而言,如果网页j对网页k没有超链接,那么第k行元素Mkj=0,否则Mkj=1/#(j)。这里隐含的意思是当一个读者在浏览网页j时,有1/#(j)的可能性跳转到网页k。
。2. 如何定义M?这个问题稍显复杂,有兴趣的读者可以参见Michael Nielsen 的博文Using MapReduce to compute PageRank了解更详细的内容。在这里,我们将其简化的定义为一个描述网页间互相链接结构的超大矩阵。假设网络里有n个网页,那么我们这个矩阵就是一个n*n的方阵。矩阵的每一列代表一个网页对外的超链接情况。例如,我们定义#(j)为第j个网页对外的所有超链接的数量。那么对于矩阵M的第j列而言,如果网页j对网页k没有超链接,那么第k行元素Mkj=0,否则Mkj=1/#(j)。这里隐含的意思是当一个读者在浏览网页j时,有1/#(j)的可能性跳转到网页k。
那么如何使用Map Reduce来计算PageRank呢?虽然整个迭代的过程必须是串行的,迭代的每一步我们还是可以用Map Reduce来并行的计算的。这里也必须并行的计算因为这个矩阵和向量的规模是超大的(想象一下整个互联网的网页数量)。使用Map Reduce来计算迭代的一步实际上是用Map Reduce来计算矩阵和向量的乘法。假设我们要计算如下一个方阵和向量的乘法。其实质是将第i个向量元素的值pi乘以矩阵第i列的每一元素,然后放在矩阵元素原来的位置。最后,把矩阵第i行的所有元素相加,得到结果向量的第i个元素的值。
类似的,我们可以得到用MapReduce计算PageRank的方法:
第一步,输入的(input_key, input_value)。input_key是某个网页的编号,如j。input_value是一个列表,元素值是M矩阵的第j列元素,最后再加上一个pj,就是当前网页j的PageRank值。
第二步,Map。Mapper(input_key, input_value)所做的事情很简单,就是把pj乘以列表元素的每一个值,然后输出一组(intermediate_key, intermediate_value)。intermediate_key就是矩阵的行号,k。intermediate_value就是pj列表元素的值,即pj乘以矩阵第k行第j列的元素的值。
第三步,汇总。把所有intermediate_key相同的中间结果放到一起。即是把第k行所有的intermediate_value放在一个列表intermediate_value_list内。
第四步,Reduce。Reducer(intermediate_key, intermediate_value_list)做的事也很简单,就是把intermediate_value_list内所有的值相加。最后形成的(output_key, output_value)就是结果向量第k行的元素值。
以上就是利用Map Reduce计算PageRank的简略过程。这个过程相当粗略和不精确,只是为了揭示Map Reduce的工作过程和Google曾经用来计算PageRank的大致方法。认真的读者应该查阅其它更严谨的著作。
最后,和上述计算矩阵和向量乘法的例子相似,Map Reduce也可以用来计算两个向量的点乘。具体怎么做留给读者自己去思考,一个提示是我们所有的intermediate_key都是相同的,可以取同一个值例如1。
2.3 Data Parallelism
这是一个“算法模式”。事实上,把Data Parallelism和下节将要提到的Task Parallelism都称之为一种“算法模式”我觉得有过于笼统之嫌。到最后,哪一种并行算法不是被分解为并行执行的task呢(task parallelism)? 而并行执行的task不都是处理着各自的那份数据吗(data parallelism)?所以如果硬要把Data Parallelism和Task Parallelism称为两种算法模式,我只能说它们的地位要高于其它的算法模式。它们是其它算法模式的基础。只不过对于有些问题而言,比较明显的我们可以把它看成是Data Parallelism的或是Task Parallelism的。也许Data Parallelism模式和Task Parallelism模式特指的就是这类比较明显的问题。
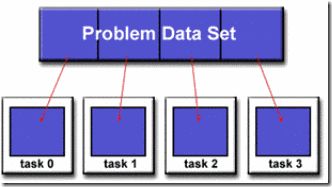
那么什么是Data Parallelism? 顾名思义,就是这类问题可以表达为同样的一组操作被施加在不同的相互独立的数据上。
一个比较典型的例子就是计算机图形学里面的Ray tracing算法。Ray tracing算法可以大致描述为从一个虚拟相机的光心射出一条射线,透过屏幕的某个像素点,投射在要渲染的几何模型上。找到射线和物体的交点后,再根据该点的材料属性、光照条件等,算出该像素点的颜色值,赋给屏幕上的像素点。由于物体的几何模型很多个小的三角面片表示,算法的第一步就是要求出射线与哪个三角面片有交点。射线与各个单独的三角面片求交显然是相互独立的,所以这可以看做是Data Parallelism的例子。
2.4 Task Parallelism
Task Parallelism的算法模式可以表述为,一组互相独立的Task各自处理自己的数据。和Data Parallelism不同,这里关注的重点不是数据的划分,而是Task的划分。
如前所述,Task Parallelism和Data Parallelism是密不可分的。互相独立的Task肯定也是运行在互相独立的数据上。这主要是看我们以什么样的视角去看问题。例如,上一节RayTracing的例子中,我们也可以把射线和一个独立的三角面片求交看作是一个独立的Task。这样就也可以当它做是Task Parallelism的例子。然而,咬文嚼字的去区分到底是Task Parallelism还是Data Parallelism不是我们的目的,我们关注的应该是问题本身。对于某一个具体问题,从Data Parallelism出发考虑方便还是从Task Parallelism出发考虑方便,完全取决于问题本身的应用场景以及设计人员自身的经验、背景。事实上,很多时候,不管你是从Task Parallelism出发还是从Data Parallelism出发,经过不断的优化,最终的解决方案可能是趋同的。
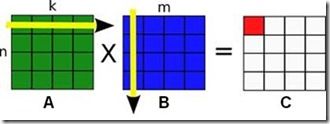
下面一个矩阵乘法的例子很好的说明了这个问题。我们都知道矩阵乘法的定义:假如有n行k列的矩阵A乘以k行m列的矩阵B,那么我们可以得到一个n行m列的的矩阵C。矩阵C的第n行第m列的元素的值等于矩阵A的第n行和矩阵B的第m列的点乘。
从Task Parallelism的角度出发,我们可能把计算C的每一个元素当做一个独立的Task。接下来,为了提高CPU的缓存利用率,我们可能把邻近几个单元格的计算合并成一个大一点的Task。从Data Parallelism的角度出发,我们可能一开始把C按行分成不同的块。为了探索到底怎样的划分更加有效率,我们可能调整划分的方式和大小,最后,可能发现,最有效率的做法是把A,B,C都分成几个不同的小块,进行分块矩阵的乘法。可以看到,这个结果实际上和从Task Parallelism出发考虑的方案是殊途同归的。
2.5 Recursive Splitting
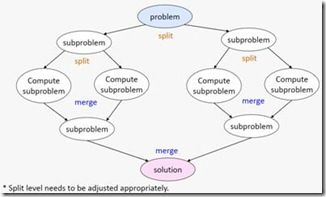
Recursive Splitting指的是这样一种算法模式:为了解决一个大问题,把它分解为可以独立求解的小问题。分解出来的小问题,可能又可以进一步分解为更小的问题。把问题分解到足够小的规模后,就可以直接求解了。最后,把各个小问题的解合并为原始的大问题的解。这实际上是我们传统的串行算法领域里面也有的“divide and conquer”的思想。
举两个例子。第一个是传统的归并排序。例如,要排序下面的8个元素的数组,我们不管三七二十一先把它一分为二。排序4个元素的数组还是显得太复杂了,于是又一分为二。现在,排序2个元素的数组很简单,按照大小交换顺序就行。最后,把排好序的数组按序依次组合起来,就得到我们最终的输出结果。
第二个例子稍微有趣一点,是一个如何用程序解“数独”游戏的例子。“数独”就是在一个9*9的大九宫格内有9个3*3的小九宫格。里面有些格子已经填入了数字,玩家必须在剩下的空格里也填入1到9的数字,使每个数字在每行、每列以及每个小九宫格内只出现一次。
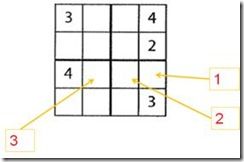
这里作为举例说明,我们考虑一个简单一点的情况:在一个4*4的格子里填入1~4的数字,使其在每行、每列以及每个2*2的格子里只出现一次。
解“数独”游戏的算法可以有很多种。如果是人来解,大概会按照上图的次序依次填入1,2,3到相应的格子当中。每填入一个新数字,都会重新按规则评估周围的空格,看能否按现有情况再填入一些数字。这个方法当然没错,不过看上去不太容易并行化。下面介绍一个按照“recursive splitting”的方法可以很容易做到并行化的解法。
1) 首先,将二维的数独格子展开成一个一维的数组。已经有数字的地方是原来的数字,空格子的地方填上“0”。 ![]()
2) 接下来,从前到后对数组进行扫描。第一格是“3”,已经有数字了,跳过。移动搜索指针到下一格。
3) 第二格是“0”,意味着我们需要填入一个新的数字。这个新的数字有4种可能性:1, 2, 3, 4。所以创建4个新的搜索分支:
4) 接下来根据现有的数字信息检查各个搜索分支。明显,第三和第四个搜索分支是非法的。因为我们在同一行中已经有了数字“3”和“4”。所以忽略这两个分支。第一和第二条分支用现有的数字检查不出冲突,所以继续从这两个分支各派生出4条新的分支进行搜索… …
这个思路像极了我们之前的归并排序的例子,都是在算法运行的过程中不断产生出新的任务。所以实际上这也是一个“Task Parallelism”的例子。
2.6 Pipeline
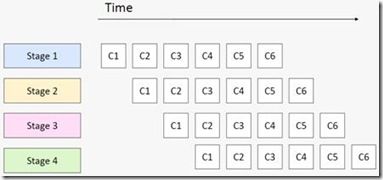
“Pipeline”也是一种比较常见的算法模式。通常,我们都会用汽车装配中的流水线、CPU中指令执行的流水线来类比的说明这一模式。它说的是我们会对一批数据进行有序、分阶段的处理,前一阶段处理的输出作为下一阶段处理的输入。每一个阶段永远只重复自己这一阶段的任务,不停的接受新的数据进行处理。用一个软件上的例子打比方,我们要打开一批文本文件,将里面每一个单词的字母全部改成大写,然后写到一批新的文件里面去,就可以创建一条有3个stage的流水线:读文件,改大写,写文件。
“Pipeline”模式的概念看上去很容易理解,可是也不是每一个人都能一下子理解的那么透彻的。例如有这样一个问题:我们有一个for循环,循环体是一条有3个stage的pipeline,每个stage的运行时间分别是10, 40, 和10个CPU的时钟间隔。请问这个for循环执行N次大概需要多长时间(N是一个很大的数)?
A. 60*N
B. 10*N
C. 60
D. 40*N
请仔细思考并选择一个答案。:-)
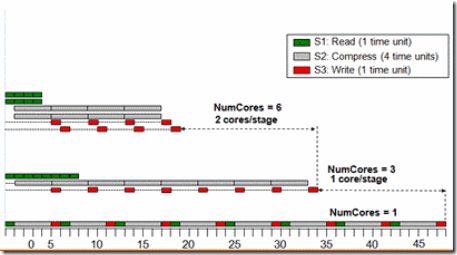
答案是40*N。流水线总的执行时间是由它最慢的一个stage决定的。原因请见下图。
2.7 Geometric decomposition
接下来这两个算法模式看上去都显得比较特殊化,只针对某些特定的应用类型。“Geometric decomposition”说的是对于一些线性的数据结构(例如数组),我们可以把数据切分成几个连续的子集。因为这种切分模式看上去和把一块几何区域切分成连续的几块很类似,我们就把它叫做”Geometric decomposition”。
最常用的例子是分块矩阵的乘法。例如,为了计算两个矩阵A,B的乘法。我们可以把他们切分成各自可以相乘的小块。
结果矩阵当然也是分块的:
结果矩阵每一分块的计算按照如下公式进行:
例如:
最终的结果就是:
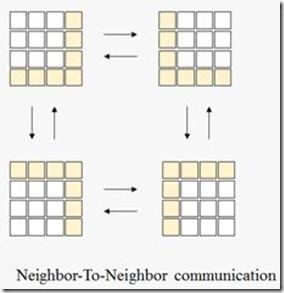
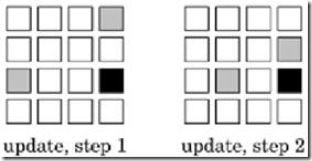
下面这幅图显示了两个4*4的分块矩阵A,B进行乘法时,计算结果矩阵C的某一分块时,需要依次访问的A,B矩阵的分块。黑色矩阵分块代表要计算的C的分块,行方向上的灰色矩阵代表要访问的矩阵A的分块,列方向上的灰色分块代表要访问的矩阵B的分块。
2.8 Non-work-efficient Parallelism
这个模式的名字取得很怪异,也有其他人把它叫做“Recursive Data”。不过相比而言,还是这个名字更为贴切。它指的是这一类模式:有些问题的处理使用传统的方法,必须依赖于对数据进行有序的访问,例如深度优先搜索,这样就很难并行化。但是假如我们愿意花费一些额外的计算量,我们就能够采用并行的方法来解决这个问题。
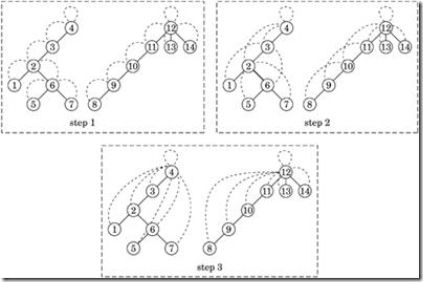
常用的一个例子是如下的“寻找根节点”的问题。假设我们有一个森林,里面每一个节点都只记录了自己的前向节点,根节点的前向节点就是它自己。我们要给每一个节点找到它的根节点。用传统的方法,我们只能从当前节点出发,依次查找它的前向节点,直到前向节点是它自身。这种算法对每一个节点的时间复杂度是O(N)。总的时间复杂度是N*O(N)。
如果我们能换一种思路来解这个问题就可以将其并行化了。我们可以给每一个节点定义一个successor(后继结点),successor的初始值都是其前向节点。然后我们可以同步的更新每一个节点的successor,令其等于“successor的successor”,直到successor的值不再变化为止。这样对于上图的例子,最快两次更新,我们就可以找到每个节点的根节点了。这种方法能同时找到所有节点的根节点,总的时间复杂度是N*log (N)。
3. 后记
如前所述,“并行编程中的设计模式”是一个仍在不断变化、发展的领域。这篇博文简要介绍了这一领域当前的发展现状,并选取八个常用的模式进行了介绍。我涉足并行编程领域不久,很多理解也并不深入。所以文章的缺点错误在所难免,真诚希望能得到大家的批评指正。
4. 参考文献
本文的写作参考了如下资源,可以作为进一步阅读的材料:
· UC Berkeley, A Pattern Language for Parallel Programming
· Eun-Gyu Kim, Parallel Programming Patterns
· Jim Browne, Design Patterns for Parallel Computation
· Tim Mattson, Patterns for Parallel Programming
· Michael Nielsen, Using Map Reduce to compute PageRank
· Aater Suleman, Parallel Programming: Do you know Pipeline Parallelism?