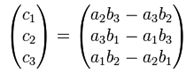罗德里格斯（Rodrigues）旋转向量与矩阵的变换

     在做双目立体视觉深度图像生成的时候，遇到旋转向量（1x3）与旋转矩阵（3x3）的概念，得知二者可以通过罗德里格斯相互转化。

1.旋转的表示

     处理三维旋转问题时，通常采用旋转矩阵的方式来描述旋转变换。旋转矩阵有以下两种方式得到。

      物体在三维空间中的旋转，可以被分为解为在直接坐标系下，分别先后围绕x,y,z坐标轴旋转得到。旋转的角度也就是我们常听到的角度roll，pitch，yew。如果已知这几个角度，就可以直接通过每一步的矩阵相乘得到整个旋转矩阵。

                              R=R(yaw)R(pitch)R(roll)

R = R ( y a w ) R ( p i t c h ) R ( r o l l )

       旋转矩阵还可以理解为围绕空间中某一个向量，直接一次旋转某一个角度得到。在openCV相机标定时得到的旋转向量r就是用这种方式。即由旋转变量来描述。

2.旋转向量得到旋转矩阵

       旋转向量的长度（模）表示绕轴逆时针旋转的角度（弧度）。旋转向量与旋转矩阵可以通过罗德里格斯（Rodrigues）变换进行转换。

       旋转角度 θ=norm(r)      （norm表示求向量r的模长）
       单位向量 (rx,ry,rz)=r/θ 
       旋转矩阵 

R=cos(θ)I+(1−cos(θ))rrT+sin(θ)∣∣∣∣∣0rz−ry−rz0rxry−rx0∣∣∣∣∣

       其中 I 为单位矩阵， rT 为 r 的转置。 
       所以 

rrT=∣∣∣∣∣rx∗rxry∗rxrz∗rxrx∗ryry∗ryrz∗ryrx∗rzry∗rzrz∗rz∣∣∣∣∣

3.根据旋转向量求另一个旋转向量

       用r表示待旋转的向量，v为旋转向量的单位向量，θ为旋转角，旋转后的向量可以表示为 

r′=rcos(θ)+(1−cos(θ))(v⋅r)v+sin(θ)(v×r)

4.根据两个旋转向量求旋转矩阵

（1）旋转角度

       已知旋转前向量为P, 旋转后变为Q。由点积定义可知：

       可推出P，Q之间的夹角为：

（2）旋转轴

       旋转角所在的平面为有P和Q所构成的平面，那么旋转轴必垂直该平面。

       假定旋转前向量为a(a1, a2, a3)， 旋转后向量为b（b1, b2, b3)。由叉乘定义得：

       所以旋转轴c(c1, c2, c3)为：

5.OpenCV实现Rodrigues变换的函数为

int cvRodrigues2( const CvMat* src, CvMat* dst, CvMat* jacobian=0 );

     src为输入的旋转向量（3x1或者1x3）或者旋转矩阵（3x3）。

     dst为输出的旋转矩阵（3x3）或者旋转向量（3x1或者1x3）。

     jacobian为可选的输出雅可比矩阵（3x9或者9x3），是输入与输出数组的偏导数。

验证代码如下：

#include 
#include 

void main()
{
    int i;
    double r_vec[3]={-2.100418,-2.167796,0.273330};
    double R_matrix[9];
    CvMat pr_vec;
    CvMat pR_matrix;

    cvInitMatHeader(&pr_vec,1,3,CV_64FC1,r_vec,CV_AUTOSTEP);
    cvInitMatHeader(&pR_matrix,3,3,CV_64FC1,R_matrix,CV_AUTOSTEP);
    cvRodrigues2(&pr_vec, &pR_matrix,0);

    for(i=0; i<9; i++)
    {
        printf("%f\n",R_matrix[i]);
    }
}

6、opencv另一种变换方法

//将旋转向量转化为旋转矩阵
Mat_ r_l = (Mat_(3, 1) << 0.04345, -0.05236, -0.01810);//左摄像机的旋转向量
Mat_ r_r = (Mat_(3, 1) << 0.04345, -0.05236, -0.01810);//右摄像机的旋转向量
Mat  R_R, R_L;
Rodrigues(r_l, R_L);
Rodrigues(r_r, R_R);

参考：

1 http://blog.csdn.net/tl_tj/article/details/47006007

2 http://blog.sina.com.cn/s/blog_5fb3f125010100hp.html

3 根据旋转前后的两个向量值，先求出旋转角度和旋转轴，然后用罗德里格旋转公式即可求出对应的旋转矩阵。 https://www.cnblogs.com/xpvincent/archive/2013/02/15/2912836.html