线性规划算法详解
线性规划
首先什么是线性规划,大致的定义我总结为在线性的目标和约束中,找出一个最优解。
举个例子:
M1和M2两种原料用于生产内外墙涂料,M1日最大可用量24吨,M2日最大可用量为6吨,外墙涂料每吨需要6吨M1,1吨M2,内墙涂料每吨需要4吨M12,吨M2,外墙涂料每吨利润5个单位,内墙涂料每吨利润4个单位。且市场需求调查数据得出,内墙日需求量不超过外墙的日需求量+1吨,内墙最大日需求量为2吨
怎样在这样的各个线性的条件中,得到最优的内外墙生产吨数,就是我们线性规划算法要做的事情。
设外墙生产x1吨,内墙生产x2吨,设利润为z,要得到z的最大化,也就是最优解,上述条件罗列为公式可得出
- 6x1+4x2<=24
- x1+2x2<=6
- -x1+x2<=1
- x2<=2
- x1,x2>0
- z=5x1+4x2
如何从这个公式中求出最优解?有以下两大方法
图解法
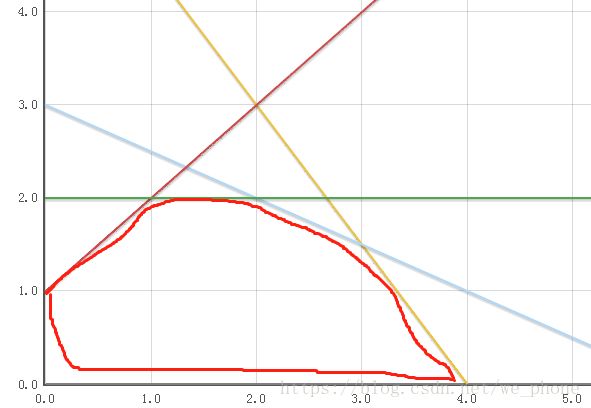
我们将上述约束条件画图,y轴为x2,x轴为x1,得出如下:
圈红色的部分就是所有的可行解,表示这个区间内都的x1x2能满足约束条件
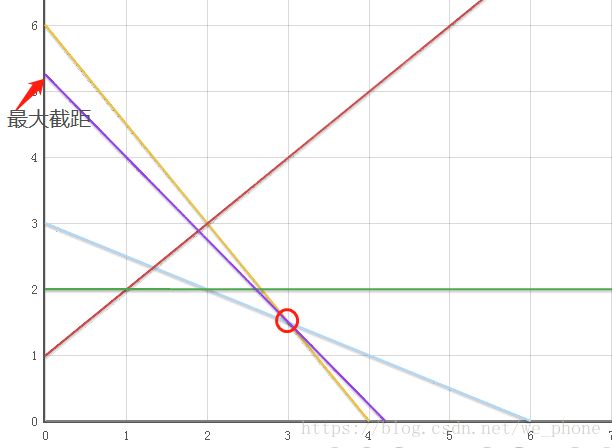
对于我们的z函数,其实表示的是一条截距为z斜率为-(5/4)的线性直线,我们要求z最大化的最优解,就是在所有的可行区域内找到可以满足z曲线截距最大的点。
最后我们发现,可行区域内能让z函数达到最大截距的点就是我圈出来的那个角点,z再增大的话,就超出可行区域了,所以不满足要求,所以最终得出最优解为x1=3,x2=1.5
这就是图解法的做法,一个定理就是,线性规划的最优解总是发生在约束几何平面的角点上,例如上面圈出来的点,先当做是个定理,我也不知道怎么证明这个定理。
以上就是线性规划的图解法,优点是简单明了,缺点就是当参数超过3个时,我们很难直观画出一个jihe几何平面来找角点,所以我们需要下面的另一种解法。
单纯形法
当超过3个参数时,单纯形法就派上用场了,单纯形法首先要做的就是把方程化为标准形式:
- 所有的变量都是非负数
- 所有的约束都是等式(非负限制除外),且具有非负的右端项
像上述的方程,如果化为标准形式,将会是如下
- 6x1+4x2+s1=24
- x1+2x2+s2=6
- -x1+x2+s3=1
- x2+s4=2
- z=5x1+4x2+0s1+0s2+0s3+0s4
新加入的s1-4表示的是松弛变量(非负),根据大于号小于号来决定他们的正负号
对于标准化形式,我们设有n个参数,设列举出的约束方程个数m,当m=n时,方程组就只有唯一的解,当m 例如y=x+1单独这个约束方程,那么可行解就是这条直线上的所有点,这个就是m=1,n=2的情况,如果再加上一个方程使得m=2,例如y=-x,则是唯一的解了,解为(-0.5,0.5) 由上面的定理,最优可行解必然出现在几何空间上的角点 对于一个m*n的方程组,我们另n-m个变量为0,再去在m个方程中求出其余的m个变量的值,如果有可行解,则这m个变量得出的点就是这个超几何平面的角点。 例如y=x+1,xy都非负,这里m=1我们就有两种角点情况,一种是x=0的角点,一种是y=0的角点,画图上便可只管看出。对于超3维的几何面也是如此类推,虽然我不知道如何直观证明,但这就是个定理。 所以我们线性规划最终zu做的事就是,找出适合的角点,并代入最优的z方程,哪个得出的z最优,哪个角点就是我们的最优解! 但当参数十分多时,角点的数量就十分庞大,所以我们需要一个智能的搜索过程,来寻找出最优角点的位置。 我们每一次的寻找角点称之为迭代,每一次我们都从原点,也就是非松弛变量全为0的时候开始 我们称令(n-m)个变量为0的这些变量为非基变量,令其余的m个变量为基变量。 从原点开始,我们计算完z值后,就要选择下一个角点来计算z,那么就需要迭代,选择一个基变量进行离基操作,并选择一个非基变量代替它,进行进基操作,从而得到下一个角点来计算z。 对于如何选择进基变量和离基变量,我们遵照如下条件 最优条件确定进基变量,在z方程上,选择一个能让z最可能往最优方向发展的变量进基,例如max z=3x1+5x2,x2的系数更高,x2非基(即非0)的话更能使z趋于最大化。 可行性条件确定离基变量,找出约束最小的那个进行离基,因为超过最小约束表明有约束不满足了,所以不能再往外扩展了。(具体操作是进行最小非负比计算,后面会继续讲) 通过这两个条件,我们就可以不用暴力穷举出所有的角点进行z计算,大大减少了计算量,最后直到无最优条件可选了,再迭代时z反而会适得其反时,最优解已经得到了,求解完成。 上面讲述的只是单纯形法的思路,具体的计算步骤就是高斯-若尔当行计算 回到上面的原料公式: 由于最初我们从原点开始,所以基变量是s1-4,我们把基变量写在左侧则为 右边的系数为非基变量,左边为基变量,因为非基变量为0,所以左边的基变量的解值就是右边的常系数,也就是截距 x1的系数为5 最能达到z最大化 x1在s1的方程中系数为-6,s1行的解值/进基变量系数的非负比最小(24/6 这里为了明显显示基变量,所以把一些参数挪到了右边,挪到左边过来就是6而不是-6,这个比值代表了新的角点的截距),所以选择x1进基,s1出基 假设我们错误的选择了s2离基,那么xi新角点上,x1的值就是6,而x1等于6超过了约束,因为24-6*6<0,而s1是非负的,所以必须选择最小非负比进行离基。 以s1离基,x1进基 其实就是把右边的变量挪到左边以达到左边全基,右边全非基,也就是用x1去替代s1,s1也替代x1,以得出 这就是我们手动完成的一次进基出基操作,现在基变量在左边为x1和s2-4,解分别为4,,2,5,2,剩下的为非基变量,我们可以就此解出新的z 这是我们手算的进基离基,当参数非常庞大的时候,手算十分蛋疼,所以我们需要得出一个规律,然后可以进行编程让计算机运算。这个运算规律就叫高斯-若尔当行运算 首先要把各个参数转到一个矩阵里,换位标准形式的原料公式的矩阵如下,一个规律是z行基本变量系数均为0 s3 z不属于基变量 但为了方便表示还是写在了一起 高斯若尔当行运算规则,根据这个矩阵,选出进基离基变量后 进基变量所在列为枢纽列,离基变量所在行为枢纽行,行列交叉位置为枢纽元素,例如我上面标蓝色的6 其实这只是对我们刚才的手算的一个推导整理,上述矩阵进行一次迭代后如下 s3 对比我们刚手算的迭代 你可以看到规律 一直不停循环迭代 直到没有最优条件时,z就是最优解,基变量的值,也就是解,在最后的最优解中,松弛变量如果大于0,说明该资源是充足的,如果等于0说明该资源是匮乏的 至此我们的线性规划代数解法就完成了绝大部分 上面讲述的是基本通用的线性规划解法,但存在一些特殊情况需要特殊处理 当所有约束都是<=或者>=时,进行标准化直接加上松弛变量即可,但存在一些既有<=又有=,>=的方程时,就会出现个别的方程没有松弛变量,这时就出现了无法标准化的坏状态。 做法是在没有松弛变量的行里加入人工变量Ri,并在z函数中给人工变量加一个惩罚系数M,M为无穷大或无穷小(根据z是max还是min决定),使人工变量在一次次迭代后化为0,若化不为0,说明无解。 这里需要进行两个阶段 第一个阶段 先不求z,而是求min r=人工变量和 若能产生r=0 则这个阶段产生了基本可行解,人工变量可以直接去掉然后进入第二阶段 第一步min r行的计算,就会遇到z行(这里是r行)基本变量系数不为0的情况,会导致z行等式不成立,所以第一步要先进行替换(假设人工变量有R1 R2两个) 正确r行=原始r行+(1*R1行+1*R2行) 进行系数化0 最后r=0时,得到的基本解,人工变量必须是非基本解,才能完全不让他进入第二阶段,万一出现人工变量为基本解但值为0导致得出r=0时,需要再选择一个0基本人工变量进行离基,选择任意一个非人工非基变量进行进基,直到迭代到所有0人工变量do都被去掉。 第二阶段 开始求z行 阶段一最后一步得出的基本变量继续作为阶段二的基本变量 同样 如果出现z行基本变量系数不为0,会导致z行等式不成立,需要进行系数化0,新行=旧行+(对应非零系数*对应基本变量行) 最后再一次迭代即可进行求z最优解 个人觉得人工变量是比较复杂而且特殊步骤比较多的,我后面会继续完善例子 两次以上得出z的值是相同的,则为退化现象,退化有时候会产生死循环的可能,退化的出现意味着至少有一个基变量在下一次迭代中变为0,基变量出现0会导致最小非负比循环出现(都是0),而且z的下次迭代继续保持原值。 实际生活的条件约束中,出现一直死循环的情况很少,几乎不会发生。 按图解法来看,当z的斜率和某个边界线的斜率相同时,则会出现一段直线上的点都是最优解,即是无穷多个解 按代数法的思路,就是出现非基变量的系数为0,这种情况下,这个非基变量可以随意进基但不改变z值,但会改变各个变量系数,这同样表现出有无限多个解的情况 按图解法来看,就是有个地方没有约束,z可以不断增加或者减少下去 代数法上的表现是,最小非负比不存在,无法选择离基变量,解和系数的比值都是0或负数,导致可以无限增大进基变量而不破坏约束,也就是无界的情况 人工变量>0 以上是我对线性规划的理解,纯手打,篇幅较大,如果有什么理解错误或者改进欢迎留言。后续我会继续完善一些例子以便理解和编写相应的代码实现。 几何角点的代数定义
进基离基
高斯-若尔当行运算
基变量
z系数
x1系数
x2系数
s1系数
s2系数
s3系数
s4系数
解值
z
1
-5
-4
0
0
0
0
0
s1
0
6
4
1
0
0
0
24
s2
0
1
2
0
1
0
0
6
0
-1
1
0
0
1
0
1
s4
0
0
1
0
0
0
1
2
基变量
z系数
x1系数
x2系数
s1系数
s2系数
s3系数
s4系数
解值
z
1
0
-2/3
5/6
0
0
0
20
x1
0
1
2/3
1/6
0
1
0
4
s2
0
0
4/3
-1/6
1
0
0
2
0
0
5/3
1/6
0
1
0
5
s4
0
0
1
0
0
0
1
2
特殊情况
无法直接标准化
退化
无穷多个解
无界解
不可行解
总结