数据结构与算法--栈、队列(队列)

Hello,everybody.我们又见面了。今天我们来学习一下队列这个数据结构，let’s Go,开始我们的征程吧。

首先，举两个生活中的常见例子。相信大家，在用电脑工作娱乐时，都会碰到这样的现象。当我们点击程序或进行其他操作时，电脑处于死机状态。正当我们准备Reset时，它突然像打了鸡血似的，突然把刚才我们的操作，按顺序执行了一遍。之所以会出现这个现象，是因为操作系统的多个程序，需要通过一个管道输出，而按先后顺序排队造成的。

还有有个例子，在我们打客服热线时，有时会出现等待的现象。当其他客户挂断电话，客服人员才会接通我们的电话。因为客服人员相对于客户而言，总是不够的，当客户量大于客服人员时，就会造成排队等待的想象。

操作系统、客服系统，都是应用了一种数据结构才实现了这种先进先出的排队功能，这个数据结构就是队列。

队列（Queue）：是只允许在一端进行插入操作，在另一端进行删除操作的线性表。

队列也是一种特殊的线性表，是一种先进先出的线性表。允许插入的一端称为表尾，允许删除的一端称为表头。

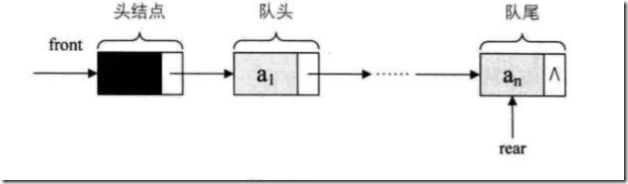
上图，很形象的表示了队列的结构。排在前面的先出，排在后面的后出。换句话，先进的先出，后进额后出。我们在队尾插入数据，队头删除数据。

 

队列的抽象数据类型:

同样是线性表，队列也有类似线性表的操作，不同的是，插入操作只能在队尾，删除操作只能在队头。

上图是队列的抽象数据类型。

顺序存储的队列:

我们在学习线性表时，知道线性表分为顺序存储与链式存储两种存储方式。队列是特殊的线性表，所以它也分为两种存储方式。我们先来看看它的顺序存储结构吧。

队列顺序存储的不足:

假设有n个元素，我们需要初始化一个长度大于n的数组，来存放这n个元素，下标为0的位置为队头。队列的插入（入队）操作，是在队尾进行操作的，队列中的其他元素不用移动。入队操作的时间复杂度为O【1】.但是如果，是删除(出队)操作，需要在队头操作，需要移动队列中所有元素，以确保我们队头(下标为0的位置)不为空。所以，时间复杂度为O【n】。

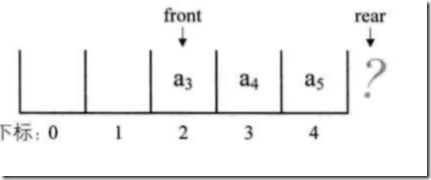
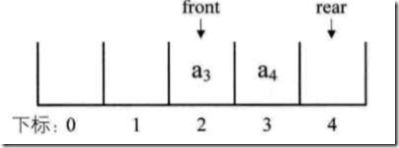
我们可以改进一下这个队列，以提高它的效率。我们大可不必，把元素放在数组的前n个位置。也就是说，我们没必要把下标为0的位置定位队头位置。如下图:

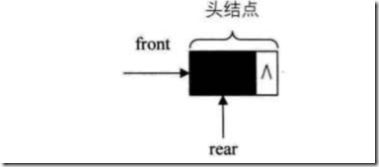
为了避免当只有一个元素时，队头与队尾重合，影响我们的操作。所以，我们引入了front、rear指针。front指向第一个元素的位置，rear指向最后一个元素的下一个位置。

这样，当rear=front时，不是队列中只有一个元素，而是队列为空。

这样我们在进行出队操作时，队列中其他元素就不用动了。我们的时间复杂度为o[1].

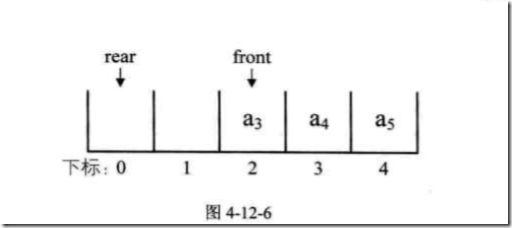
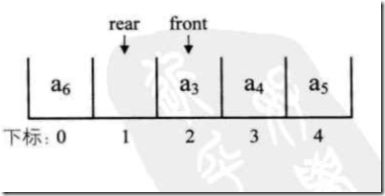
但是，我们的问题又来了，看下图:

此时，rear已经超出了数组的界限，但是下标为0、1的位置还是空的，这样是不是挺浪费的？此时，我们的循环队列就横空出世了。

循环队列:队列的头尾相接的顺序存储结构称为循环队列.

如下图:

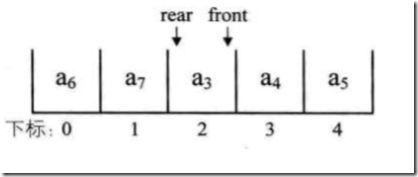
这里有一个问题，大家看下图:

此图中，rear=front，此时队满。可是，我们刚才说rear=front时，队列为空。那么，rear=front时，是空还是满呢？对于这个问题，我们提供了2中解决方法。

方法一:初始化一个flag变量，当flag=1,rear==front时，队列满。当flag=0,rear==front时,队列空。

方法二:当rear==front时，队列为空。当rear与front中间仅差一个存储单元时，队列为满。

这里，我们讨论一下方法二。看下图:

front与rear之间相处一个存储单元，此时我们就说队列已满。因为rear有时>front，有时

(rear+1)%QueueSize==front.

当rear>front时，rear-front就是队列的长度。如下图:

当rear

将两部分加在一起，就是队列的长度。最后，我们得出计算队列长度的通用公式：

(rear-front+QueueSize)%QueueSize

我们看一下循环队列的顺序存储结构代码:

typedef int QElemType

typedef struct

{

    QElemType data[MAXSIZE];

     int front;

    int rear;

}SqQueue;

 

循环队列的初始化代码:

Status InitQueue(SqQueue *Q)

{

     Q->front=0;

   Q->rear=0;

return ok;

}

 

循环队列求队列长度:

int QueueLength(SqQueue Q)

{

     return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;

}

循环队列的入队操作

Status EnQueue(SqQueue *Q,QElemType e)

{

          if((Q->rear+1)==Q->front)/*队列满的判断*/

         return ERROR;

       Q->data[Q->rear]=e;

     Q-rear=(Q->rear+1)%MAXSIZE

return Ok;

}

循环队列的出队操作

Status DeQueue(SqQueue *Q,QElemType *e)

{

        if(Q->front=Q->rear)/*队列空的判断*/

           return ERROR;

          *e=Q->data[Q->front];

        Q->front=(Q->front+1)%MAXSIZE;

     return ok;

}

从这一段讲解，我们发现，单单使用队列的顺序存储结构，性能是不高的。我们应该使用循环队列，但是循环队列又面临着数组溢出的问题，所以我们还有学习一下不用队列长度的链式存储结构。

队列的链式存储:

队列的链式存储，其实就是线性表的单链表。只不过，只能尾进头出。我们把它简称为链队列。为了操作的方便，我们把front指向头结点，把rear指向终端结点。空队时，front、rear都指向头结点。如下图:

链队列的结构:

typedef int QElemType;

/*结点的结构*/

typedef struct QNode

{

         QElemType   data;

         struct   QNode  *next;

}QNode,*QueuePtr;

 

/*链表的结构*/

typedef struct

{

         QueuePtr  front,  rear;

}LinkQueue;

 

链队的入队操作:

Status EnQueue(LinkQueue *Q,QElemType e)

{

           QueuePtr  s=(QueuePtr)malloc(size(QNode));

          if(!s)/*存储分配失败*/

          exit(OVERFLOW);

         s->data=e;

       s->next=NULL;

         Q->rear->next=s;

       Q->rear=s;

return ok;

}

链队的出对操作:

Status DeQueue(LinkQueue *Q,QElemType *e)

{

         QueuePtr  P;

       if(Q-front==Q->rear)

return ERROR;

   P=Q->front-next;

*e=p->data;

Q->front->next=p->next;

if(Q->rear==p)

  Q->rear=Q->front;

  free(p);

return ok;

}

我们来比较一下循环队列与链队的区别:

关于他们的区别，我们从两方面来分析。时间、空间。

时间:时间复杂度都为O【1】,但是链队在申请、释放结点时会消耗一些时间。

空间:循环队列需要固定的长度，会出现存储元素数量，空间浪费的问题。链队不会出现空间浪费的问题。

总的来说，当我们可以确定长度时，我们选择循环队列，否则使用链队。

总结:

这一章，我们主要学习的数据结构是栈(stack)、队列(Queue).

Stack：只允许在一端进行插入删除操作。

Queue:只能在一端插入，另一端删除。

Stack、Queue都是特殊的线性表。所以它们都可以用顺序存储结构来实现，但是都存在一些弊端。它们各自都有解决这些弊端的方法。

Stack,它把相同的数据类型的栈，存放在一个数组中，让数组一头为一个栈的栈顶，另一头为另一个栈的栈顶。最大化的利用了数组空间。

Queue:为了避免出队，而移动队元素，于是引入了循环队列，让头尾相连。使得时间复杂度为O【1】.

他们又都可以用链式存储结构实现。

这就是这一章的内容了，接下来我们一起学习串。

转载于:https://www.cnblogs.com/VitoCorleone/p/3784468.html