《集体智慧编程》读书笔记4

最近重读《集体智慧编程》，这本当年出版的介绍推荐系统的书，在当时看来很引领潮流，放眼现在已经成了各互联网公司必备的技术。
这次边阅读边尝试将书中的一些Python语言例子用C#来实现，利于自己理解，代码贴在文中方便各位园友学习。

由于本文可能涉及到的与原书版权问题，请第三方不要以任何形式转载，谢谢合作。

第四部分 优化

本篇中将介绍一种名为随机优化的技术。随机优化技术适合处理这样一类问题：问题受多种变量影响，有多种可能的解，多种变量和多种解之间可能产生很多种组合。优化算法通过尝试计算不同解，并给解打分以确定其质量的方式来寻找问题的最优解。优化算法主要针对的场景就是问题有太多可能的解，以至于无法一一尝试的情况，优化算法会以对解有改正的方式来逐步修正解最终得到较优的解。
下面将以几个典型的例子来介绍优化算法

组团旅游

组团旅游问题的目的是为来自不同地方去往同一地点的人们规划合理的出行方式。并且成员们将在同一天离开。在每个成员的家到目的地机场之间都有许多航班，这些航班的起飞时间不同，价格和续航也不相同。

输入

首先在类Travel中添加如下表示游客，目的的代码：

public class Travel
{
    public List> People { get; } = new List>()
    {
        Tuple.Create("Seymour", "BOS"),
        Tuple.Create("Franny", "DAL"),
        Tuple.Create("Zooey", "CAK"),
        Tuple.Create("Walt", "MIA"),
        Tuple.Create("Buddy", "ORD"),
        Tuple.Create("Les", "OMA")
    };

    // New York的LaGuardia机场 
    private string _destination = "LGA";
}

而航班数据存放在文件schedule.txt中，可以点此下载。
文件中每一行都是如下这样的数据：

LGA,OMA,6:19,8:13,239

逗号分隔的5个列，分别表示起点、终点、起飞时间、到达时间和价格。在Travel添加表示航班的_flights成员并完成用于从文件加载数据初始化_flights的函数。

private Dictionary>> _flights
    = new Dictionary>>();

public void PopulateFlights(string filename)
{
    using (var fs = new FileStream(filename, FileMode.Open))
    {
        var sr = new StreamReader(fs);
        while (!sr.EndOfStream)
        {
            var line = sr.ReadLine();
            if (!string.IsNullOrEmpty(line))
            {
                var vals = line.Split(',');
                var key = $"{vals[0]}-{vals[1]}";
                if (!_flights.ContainsKey(key))
                    _flights.Add(key, new List>());
                // 将航班详情添加到航班列表
                _flights[key].Add(Tuple.Create(vals[2], vals[3], int.Parse(vals[4])));
            }
        }
    }
}

接着实现一个简单的函数用于计算上面一个时间在一天中的分钟数。这个函数使下一步计算起飞到达两个时间的之间的耗时变得容易。

private int GetMinutes(string t)
{
    var x = t.Split(':');
    return int.Parse(x[0]) * 60 + int.Parse(x[1]);
}

上面这些就是程序所需的输入。下一步将结合航班的票价，候机时间，旅行时间等因素来寻找最优结果。

输出

本例中我们用两个数字来表示用户的出行方式，第一个数字表示去程航班的索引，第二个表示返程航班的索引。最终多人的结果将汇总成一个数组，而这个数组的长度将是团员数量的两倍。
这里我们还实现了一个方法用于将结果数组打印为易于读懂的形式：

public void PrintSchedule(List r)
{
    for (int d = 0; d < r.Count / 2; d++)
    {
        var name = People[d].Item1;
        var origin = People[d].Item2;
        var key = $"{origin}-{_destination}";
        var keyRet = $"{_destination}-{origin}";
        var @out = _flights[key][r[2 * d]];
        var ret = _flights[keyRet][r[2 * d + 1]];
        Console.Write($"{name.PadLeft(10)}{origin.PadLeft(10)} ");
        Console.Write($"{@out.Item1.PadLeft(5)}-{@out.Item2.PadLeft(5)} ${@out.Item3.ToString().PadLeft(3)} ");
        Console.WriteLine($"{ret.Item1.PadLeft(5)}-{ret.Item2.PadLeft(5)} ${ret.Item3.ToString().PadLeft(3)}");
    }
}

成本函数

成本函数是优化算法解决问题的关键，也是算法中最难实现部分。优化算法的目标就是寻找让成本函数返回结果达到最小化的输入（本例中为航班信息），因此成本函数要返回一个值表示方案的好坏（值越大表示方案越差，而对于好坏程度，即值的大小程度不做考虑）。

本例中决定成本函数输出的几个变量如下：

• 价格 ： 所有航班的总票价（更复杂的情况，是考虑财务因素后的加权平均）
• 旅行时间 ： 每个人在飞机上花费的总时间
• 等待时间 ： 在机场等待其他成员到达的时间
• 出发时间 ： 早上太早起飞的航班也许会产生额外的成本。
• 汽车租用时间 ： 如果集体租用车辆，必须在一天内早于起租时刻前将车辆归还

对于应用优化算法的问题找到这些决定成本的因素及确定其重要性非常重要。对于任何问题只要确定了这些，都可以套用本节所描述的优化算法。
确定好影响成本的变量后，接着就要想办法将它们组合形成一个值。组合的办法就是确定如在飞机上时间或在机场等待耗时的价值是多少，如假设每在飞机上节省一分钟价值1美元，而在机场等待每节省1分钟价值0.5美元。根据上面描述我们实现如下的成本计算函数：

public float ScheduleCost(List sol)
{
    var totalprice = 0f;
    int latestArrival = 0;
    int earliestDep = 24 * 60;

    for (int d = 0; d < sol.Count / 2; d++)
    {
        //得到去程航班和返程航班
        var origin = People[d].Item2;
        var outbound = _flights[$"{origin}-{_destination}"][sol[2 * d]];
        var returnf = _flights[$"{_destination}-{origin}"][sol[2 * d + 1]];

        //总价等于所有人往返航班价格之和
        totalprice += outbound.Item3;
        totalprice += returnf.Item3;

        //记录最晚到达时间和最早离开时间
        if (latestArrival < GetMinutes(outbound.Item2))
            latestArrival = GetMinutes(outbound.Item2);
        if (earliestDep > GetMinutes(returnf.Item1))
            earliestDep = GetMinutes(returnf.Item1);
    }
    //每个人必须在机场等待直到最后一个人到到达为止
    //他们也必须在相同时间到达，并等候他们的返程航班
    var totalwait = 0f;
    for (int d = 0; d < sol.Count / 2; d++)
    {
        var origin = People[d].Item2;
        var outbound = _flights[$"{origin}-{_destination}"][sol[2 * d]];
        var returnf = _flights[$"{_destination}-{origin}"][sol[2 * d + 1]];
        totalwait += latestArrival - GetMinutes(outbound.Item2);
        totalwait += GetMinutes(returnf.Item1) - earliestDep;
    }

    //如果需要多支付一天的汽车租赁费用，则总价加50
    if (latestArrival < earliestDep) totalprice += 50;

    return totalprice + totalwait;
}

可以根据自己的需要调整每种成本的权重或增加其他成本因素。

这段代码使用了译注中修正后的代码，即倒数第二行不是>而是小于<。这样代码latestarrival < earliestdep正是表示第二天最早的出发时间比第一天的最晚到达时间的时刻要晚，可能会产生超过24小时的租车时间（要把latestarrival和earliestdel理解为不在同一天）

成本的函数的输入就是前文介绍的输出解，成本函数正是对一个解进行成本计算。我们使用原书的示例输出解来测试这个成本函数，代码如下：

var traval = new Travel();
traval.PopulateFlights("schedule.txt");
var cost = traval.ScheduleCost(new List {1, 4, 3, 2, 7, 3, 6, 3, 2, 4, 5, 3});
Console.WriteLine(cost);

通过上面成本函数和测试代码，我们已经很明确，优化算法的目的就是找出一个使成本最小的输出序列。
本例中一共有120趟不同时间提供给不同团员的航班，可能的组合会有10^12之多，所以尝试所有这些组合几乎是不现实的，而这正是下面介绍的优化算法的用武之地。

优化算法1 - 随机搜索

随机搜索不是一种非常好的算法，但其可以是我们容易理解这类算法的意图，并且可以作为评估其他算法优劣的基线。
随机算法的实现函数接收两个参数，第一个参数domain是一个二元组列表，元组中指定了随机变量选取范围的最大值和最小值。由于每位团员都有10个去程航班和10个返程航班可选，所以domain的所有元组都是(0,9)。
另外domain列表的长度与输出解的长度相同，前文介绍输出时提到，由于航班是往返的，输出解的长度为团员人数的2倍即12，所以domian列表的长度也是12。
而第二个参数就是成本函数，本例中即为ScheduleCost。
函数执行中会随机调用1000次成本函数，并会记录最佳猜测（成本最低的输出解）并将其返回。

public List RandomOptimize(List> domain, Func, float> costf)
{
    var best = 999999999f;
    List bestr = null;
    var random = new Random();
    for (int i = 0; i < 1000; i++)
    {
        //创建一个随机解
        var r = domain.Select(t => random.Next(t.Item1, t.Item2)).ToList();
        //得到成本
        var cost = costf(r);
        //与目前为止最优解进行比较
        if (cost < best)
        {
            best = cost;
            bestr = r;
        }
    }
    return bestr;
}

虽然1000次猜测只占全部可能性中很小的一部分，但仍有可能找到不算很差的解（虽然不是最优）
下面是测试函数，每次执行的结果应该都不太一样：

var traval = new Travel();
traval.PopulateFlights("schedule.txt");
var domain = Enumerable.Repeat(Tuple.Create(0, 9), traval.People.Count*2).ToList();
var s = traval.RandomOptimize(domain, traval.ScheduleCost);
var cost = traval.ScheduleCost(s);
Console.WriteLine(cost);
traval.PrintSchedule(s);

下面的输出是在楼主电脑上运行时得到的1000次随机下最好的结果：

3748
   Seymour       BOS 18:34-19:36 $136 12:08-14:05 $142
    Franny       DAL 15:44-18:55 $382  9:49-13:51 $229
     Zooey       CAK 13:40-15:38 $137 10:32-13:16 $139
      Walt       MIA 15:34-18:11 $326 12:37-15:05 $170
     Buddy       ORD 12:44-14:17 $134  9:11-10:42 $172
       Les       OMA 15:03-16:42 $135 11:07-13:24 $171

可以试试进行10000次随机尝试，看是否会出现更好的结果。

爬山法

在我们当前的例子中，较优的解之间应该是存在相似性的。而上面介绍的随机法中，没有充分利用已找到的较优解来去发现相似的更优的解。而这一部分介绍的爬山法会在这方面有改进。
爬山法从一个随机解开始，然后在其临近的解集中寻找更好的解，这样会比反复随机去尝试成本更低。这种由一点逐渐寻找成本更低的解类似于走下坡路，然后这不会无限制的下去，一定有一点开始周围的解成本开始变高，这就类似遇到山坡。所以这种方法被称为爬山法。而我要找的就是这个最低的点。
具体到问题上的做法就是先随机选定一个时间安排，然后再找到所有与之相邻的安排（即相邻的航班），然后对这些相邻的安排进行成本计算，其中具有最低成本的安排将成为新的解，然后在这个解基础上继续重复上面的计算直到没有相邻的安排能够改善成本为止。算法实现如下：

public List HillClimb(List> domain, Func, float> costf)
{
    //创建一个随机解
    var random = new Random();
    var sol = domain.Select(t => random.Next(t.Item1, t.Item2)).ToList();

    //主循环
    while (true)
    {
        //创建相邻解的列表
        var neighbors = new List>();
        for (int j = 0; j < domain.Count; j++)
        {
            //在每个方向上相对于原值偏离一点
            if (sol[j] > domain[j].Item1)
                neighbors.Add(sol.Take(j).Concat(new[] { sol[j] - 1 }).Concat(sol.Skip(j + 1)).ToList());
            if (sol[j] < domain[j].Item2)
                neighbors.Add(sol.Take(j).Concat(new[] { sol[j] + 1 }).Concat(sol.Skip(j + 1)).ToList());
        }
        //在相邻解中寻找
        var current = costf(sol);
        var best = current;
        foreach (var n in neighbors)
        {
            var cost = costf(n);
            if (cost < best)
            {
                best = cost;
                sol = n;
            }
        }
        if (best == current)
            break;
    }
    return sol;
}

算法针对随机解，生成最多24个邻近的解（由于随机解可能有在边界的情况，不会添加邻近的解，这样可能不足24个）。然后在这些解中寻找最优的解。找出的最优解将继续重复这个过程，直到不再出现最优解。
把测试代码中的优化算法换成如下来试试结果：

var traval = new Travel();
traval.PopulateFlights("schedule.txt");
var domain = Enumerable.Repeat(Tuple.Create(0, 9), traval.People.Count*2).ToList();
var s = traval.HillClimb(domain, traval.ScheduleCost);
var cost = traval.ScheduleCost(s);
Console.WriteLine(cost);
traval.PrintSchedule(s);

在楼主电脑上执行的结果如下，注意这个结果也是随机的：

2747
   Seymour       BOS 12:34-15:02 $109 10:33-12:03 $ 74
    Franny       DAL 10:30-14:57 $290  9:49-13:51 $229
     Zooey       CAK 12:08-14:59 $149 13:37-15:33 $142
      Walt       MIA 11:28-14:40 $248  8:23-11:07 $143
     Buddy       ORD 12:44-14:17 $134  7:50-10:08 $164
       Les       OMA 12:18-14:56 $172  8:04-10:59 $136

可以看到，爬山法得到的结果比随机法好很多。
但是爬山法有个很大的缺陷。由于爬山法是沿着一个“下坡”向下找，而所在的这个“谷”是有第一次随机确定的，而这个谷有很大的可能并不是全局最低的那个，即很有可能爬山法得到的不是全局最优解。
而改进这个问题最简单的一个方法就是，随机产生多个解并使用多个随机解进行“爬山”，借此有更大的希望可以找到更接近全局最优解的解。
后面会介绍另外两种可以避免陷入局部最小值的方法：模拟退火算法和遗传算法。

模拟退火算法

模拟退火算法是受物理学领域启发而被发现的一种优化算法。退火是指将合金加热后再慢慢冷却的过程。原子受热而向周围活跃，又逐渐稳定到一个低能阶的状态。
模拟退火算法也是由一个随机解开始，用一个变量表示温度，这一温度一开始非常高，然后逐渐变低。每一次迭代过程中，算法会随机选中题解中某个数字并朝某个方向变化，然后计算变化后的解的成本并与当前解的成本比较。然后最关键部分的就在于 - 成本更低的新解会被选作当前题解，而成本更高的题解仍有可能成为当前题解。这正是避免陷入爬山法中那种局部最小的一种方法。在某些情况下，在得到一个更优解前转向一个更差的解是有必要的。
模拟退火算法在退火过程开始阶段会接受表现更差的解，随着退火的不断进行，算法越来越不可能接受较差的解，直到最后其只接受更优的解。这个接受更差解的概率按照下面这个公式变化：

由于温度开始非常高，在算法中即表示接受较差解的可能性非常高，指数值接近0，函数值即概率接近1。随着温度递减，高成本和低成本之间距离如果再比较大，指数值就会上升，概率值会显著下降，算法将不再倾向非常差的解，只会接受稍差的解。
算法的实现如下：

public List AnnealingOptimize(List> domain, Func, float> costf,
    float T = 10000.0f, float cool = 0.95f, int step = 1)
{
    //随机初始化值
    var random = new Random();
    var vec = domain.Select(t => random.Next(t.Item1, t.Item2)).ToList();

    while(T>0.1)
    {
        //选择一个索引值
        var i = random.Next(0, domain.Count - 1);
        //选择一个改变索引值的方向
        var dir = random.Next(-step, step);
        //创建一个代表题解的新列表，改变其中一个值
        var vecb = vec.ToList();
        vecb[i] += dir;
        if (vecb[i] < domain[i].Item1) vecb[i] = domain[i].Item1;
        else if (vecb[i] > domain[i].Item2) vecb[i] = domain[i].Item2;
        //计算当前成本和新成本
        var ea = costf(vec);
        var eb = costf(vecb);
        //是更好的解？或是退火过程中可能的波动的临界值上限？
        if (eb < ea || random.NextDouble() < Math.Pow(Math.E, -(eb - ea) / T))
            vec = vecb;
        //降低温度
        T *= cool;
    }
    return vec;
}

算法代码中，温度和冷却率是两个可选参数（还有一个产生随机相邻解的步进值是可调的）。如果出现最优解则会接受最优解，如果解更差，在一定情况下（退火概率发生范围内）也会接受较差的解。直到冷却到一定温度，算法停止。可以用如下代码测试：

var s = traval.AnnealingOptimize(domain, traval.ScheduleCost);

整体上来说，这种方法会使成本持续下降。

遗传算法

遗传算法是受自然科学启发而被发现的算法。算法的过程大致是：先随机生成一组解，称之为种群 。在优化过程的每一步，算法会计算整个种群的成本函数，得到一个解的有序列表（按成本由低到高排序）。
上面排序后的得到的较优的解将作为下一代种群的第一批成员。而下一代种群中的其余位置将由修改较优解得到的新成员来填充。
修改较优解的方法有两种，分别为变异和配对。
变异是其中较简单的一种做法，其一般做法是对当前最优解做微小的、简单的、随机的改变。对于本例即在解中选出一个数字并递增或递减。
配对法又称交叉，这种方法是选取最优解中的前两个并按照某种方式将它们相结合。如对于本例可以取出一个解中的一部分元素和另一个解中的另一部分元素构成一个新的解。
通常我们构造的新种群中的元素数量与旧种群相同，并使用新种群重复上面的过程，直到达到指定迭代次数或数次迭代后解没有得到改善为止。

public List GeneticOptimize(List> domain, Func, float> costf,
    int popsize = 50, int step = 1, float mutprob = 0.2f, float elite = 0.2f, int maxiter = 100)
{
    var random = new Random();
    //变异操作
    Func, List> mutate = vec =>
    {
        var i = random.Next(0, domain.Count - 1);
        if (random.NextDouble() < 0.5 && vec[i] > domain[i].Item1)
            return vec.Take(i).Concat(new[] { vec[i] - step }).Concat(vec.Skip(i + 1)).ToList();
        else if (vec[i] < domain[i].Item2)
            return vec.Take(i).Concat(new[] { vec[i] + step }).Concat(vec.Skip(i + 1)).ToList();
        return vec;
    };
    //配对操作
    Func, List, List> crossover = (r1, r2) =>
    {
        var i = random.Next(1, domain.Count - 2);
        return r1.Take(i).Concat(r2.Skip(i)).ToList();
    };
    //构造初始种群
    var pop = new List>();
    for (int i = 0; i < popsize; i++)
    {
        var vec = domain.Select(t => random.Next(t.Item1, t.Item2)).ToList();
        pop.Add(vec);
    }
    //每一代中有多少胜出者？
    var topelite = (int) (elite*popsize);
    Func cf = (x, y) => x == y ? 1 : x.CompareTo(y);
    var scores = new SortedList>(cf.AsComparer());
    //主循环
    for (int i = 0; i < maxiter; i++)
    {
        foreach (var v in pop)
           scores.Add(costf(v),v);
        var ranked = scores.Values;
        //从胜出者开始
        pop = ranked.Take(topelite).ToList();

        //添加变异和配对后的胜出者
        while (pop.Count

值得注意的是，我们给SortedList传入的IComparer对象是通过一种特殊方式构造的。在本系列之前的文章中，我们也见到过需要自定义SortedList比较器的情况，那时候我们老老实实的写了个实现IComparer接口的类，并传入此类的对象给SortedList。虽说这是最正宗的方法，但楼主一直感觉这种方法开起来弱爆了。于是不甘心，搜索一番，还真在StackOverflow上发现一个有用的回答，果断借(chao)鉴(xi)来，并一并把这段代码附在这里。

public static class ComparisonEx
{
    public static IComparer AsComparer(this Comparison @this)
    {
        if (@this == null)
            throw new System.ArgumentNullException("Comparison @this");
        return new ComparisonComparer(@this);
    }

    public static IComparer AsComparer(this Func @this)
    {
        if (@this == null)
            throw new System.ArgumentNullException("Func @this");
        return new ComparisonComparer((x, y) => @this(x, y));
    }

    private class ComparisonComparer : IComparer
    {
        public ComparisonComparer(Comparison comparison)
        {
            if (comparison == null)
                throw new System.ArgumentNullException("comparison");
            this.Comparison = comparison;
        }

        public int Compare(T x, T y)
        {
            return this.Comparison(x, y);
        }

        public Comparison Comparison { get; private set; }
    }
}

可以将这个方法放在项目的公共类库中，然后就可以像例子中那个方便的去构造IComparer了。

算法有几个可选参数：

• popsize：种群大小
• mutprob：种群新成员由变异而非配对而来的概率
• elite：种群中被认为事最优解且被允许进入下一代的部分
• maxiter：需运行多少次迭代

测试算法仍然只需要修改一行代码即可：

var s = traval.GeneticOptimize(domain, traval.ScheduleCost);

可以看到算法在执行几个迭代后，最优结果趋于稳定。

上面这些算法可行有赖于另一个事实，航班列表是有序的，这样我们去尝试一个当前最优解前后的航班才可能得到更好的结果。如果航班是乱序状态，可能只有随机搜索最管用。

涉及偏好的优化

这一部分讨论一类这样的优化问题，如果将有限的资源分配给多个表达了偏好的人，并尽可能使他们都满意。这类问题都是从个体中提取信息并将其组合起来产生出优化结果。

学生宿舍优化问题

问题定义如下：有5间宿舍，每间宿舍有两个隔间，由10名学生来竞争这些住所。每一个学生都有一个首选和一个次选。
我们先在类Dorm中添加宿舍数据和学生们的选择数据：

public class Dorm
{
    // 宿舍，每个宿舍有两个隔间
    private List _dorms = new List()
    {
        "Zeus","Athena","Hercules","Bacchus","Pluto"
    };

    // 学生，以及首选和次选
    private List>> _prefs =
        new List>>()
        {
            Tuple.Create("Toby",Tuple.Create("Bacchus", "Hercules")),
            Tuple.Create("Steve",Tuple.Create("Zeus", "Pluto")),
            Tuple.Create("Andrea",Tuple.Create("Athena", "Zeus")),
            Tuple.Create("Sarah",Tuple.Create("Zeus", "Pluto")),
            Tuple.Create("Dave",Tuple.Create("Athena", "Bacchus")),
            Tuple.Create("Jeff",Tuple.Create("Hercules", "Pluto")),
            Tuple.Create("Fred",Tuple.Create("Pluto", "Athena")),
            Tuple.Create("Suzie",Tuple.Create("Bacchus", "Hercules")),
            Tuple.Create("Laura",Tuple.Create("Bacchus", "Hercules")),
            Tuple.Create("Neil",Tuple.Create("Hercules", "Athena"))
        };
}

通过数据可以看到，不可能同时满足所有学生的首选。对于这个问题所有可能的组合不算很多，但对于现实生活中的情况，如有上千的学生，百余的宿舍或宿舍有4个以上的隔间时，可能的解会多达上亿。
另外这个问题解的表示也是需要一定的技巧。我们设想每间宿舍有两个“槽”，本例中5个宿舍会有10个槽。而解就是将每个学生依次安置于各空槽内。第一个学生可置于10个槽中的任意一个，第二个学生置于剩余9个槽中之一。

我们来实现打印题解的方法，通过这个可以很清楚的看到题解的工作方式：

public void PrintSolution(List vec)
{
    var slots = new List();
    // 为每个宿舍见两个槽
    for (int i = 0; i < _dorms.Count; i++)
        slots.AddRange(new []{i,i});
    // 遍历每一个名学生的安置情况
    for (int i = 0; i < vec.Count; i++)
    {
        var x = vec[i];
        //从剩余槽中选择
        var dorm = _dorms[slots[x]];
        //输出学生及其被分配的宿舍
        Console.WriteLine($"{_prefs[i].Item1} {dorm}");
        //删除该槽
        slots.RemoveAt(x);
    }
}

方法中首先创建槽序列，每两个槽对应一间宿舍。接着遍历题解中的每个数字，并在槽序列中找到该数字（这个数字是当前状态下的槽的位置的索引）对应的宿舍号，这表示这个题解值对应的学生被安置的宿舍。然后打印这个输出，并从槽序列中删除这个位置的槽。（最后一次迭代后，槽列表将变为空，且每个学生的分配情况也已打印完毕）。
可以运行下面代码看看题解的打印情况：

var dorm = new Dorm();
dorm.PrintSolution(new List() { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 });

要注意，题解序列中每个值都应该在一个合理的范围内。如第一个值应该在0到9之间，第二个应该在0到8之间。我们在代码中添加一个定义题解范围的成员：

//题解范围
public List> Domain =>
    Enumerable.Repeat(0, _dorms.Count*2)
        .Select((v, i) => Tuple.Create(0, _dorms.Count*2 - i - 1))
        .ToList();

成本函数

成本函数的工作方式类似打印题解的函数。构造槽序列，并在计算过槽的成本后将其删除。成本值的定义为：如果题解中学生被安置的宿舍是学生的首选宿舍，则总成本不增加，如果是次选则总成本加1，而如果不在学生选择范围则总成本加3。

public float DormCost(List vec)
{
    var cost = 0;
    // 建立槽序列
    var slots=new List() {0,0,1,1,2,2,3,3,4,4};
    // 遍历每一名学生
    for (int i = 0; i < vec.Count; i++)
    {
        var x = vec[i];
        var dorm = _dorms[slots[x]];
        var pref = _prefs[i].Item2;
        //首选成本为0，次选成本值为1
        //不在选择之列，成本加3
        if (pref.Item1 == dorm) cost += 0;
        else if (pref.Item2 == dorm) cost += 1;
        else cost += 3;
        //删除该槽
        slots.RemoveAt(x);
    }
    return cost;
}

成本函数设计中我们让最优解的总成本为0（虽然按当前问题的定义不可能产生最优解），这样我们可以很清楚的看出当前解与最优解的差距，同时在找到最优解时可以停止搜索（我们知道在总成本为0的情况下一定是最优解）。

执行优化函数

有了成本函数，我们就可以使用上一节实现的优化函数来对宿舍分配问题进行求解：

var dorm = new Dorm();
var traval = new Travel();
var s = traval.RandomOptimize(dorm.Domain, dorm.DormCost);
dorm.PrintSolution(s);
Console.WriteLine("-------------------");
s = traval.GeneticOptimize(dorm.Domain, dorm.DormCost);
dorm.PrintSolution(s);

可以看到这个问题题解的最大不同就是每一个人对应的解的定义范围都在变动。
这部分的方法对于其它类似为游戏玩家分配房间，为程序员分配bug等类似分配问题都适用。

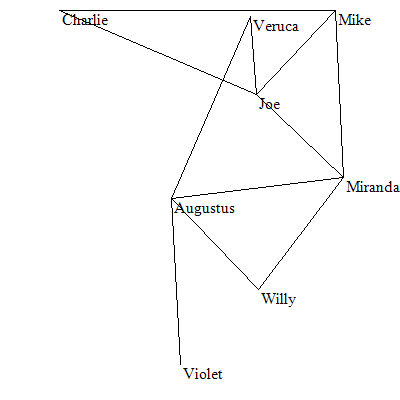
网络可视化 - 更好的布局

这个问题的目的是将图以最佳的方式绘制出来，比如下面两张图，图2明显比图1绘制的更易读。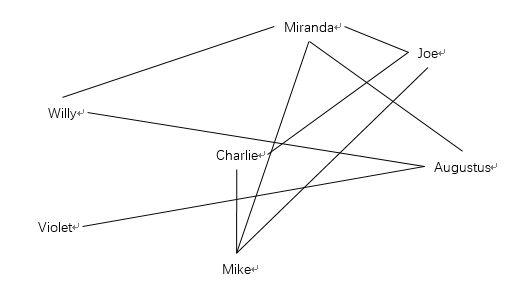
图1

图2

下面我们就来尝试实现这个优化算法，以使图1可以被更好的优化为图2的布局。
首先新建名为SocialNetwork的类，并在其中添加反映图中所示关系的数据：

public class SocialNetwork
{
    List _people = new List()
    {
        "Charlie","Augustus","Veruca","Violet","Mike","Joe","Willy","Miranda"
    };

    List _links = new List()
    {
        new[] {"Augustus", "Willy"},
        new[] {"Mike", "Joe"},
        new[] {"Miranda", "Mike"},
        new[] {"Violet", "Augustus"},
        new[] {"Miranda", "Willy"},
        new[] {"Charlie", "Mike"},
        new[] {"Veruca", "Joe"},
        new[] {"Miranda", "Augustus"},
        new[] {"Willy", "Augustus"},
        new[] {"Joe", "Charlie"},
        new[] {"Veruca", "Augustus"},
        new[] {"Miranda", "Joe"}
    };
}

绘制图2这样看起来易于理解的图的一个方法叫质点弹簧算法，这是来源于物理学建模的一种算法，其原理是各结点彼此向对方施以推力并试图分离，而结点间的连线则试图将关联结点彼此拉近。如此网络就会呈现这样一个布局：未关联的节点被推离，而关联的结点则被彼此拉近却又不会靠的得很拢。
质点弹簧算法唯一的问题在于无法避免交叉，而这正是优化算法擅长解决的问题。我们给交叉设定一个成本值，并定义一个成本函数，而用优化算法去寻找成本最低的解，则得到的结果一定是交叉最少的解。

计算交叉线

首先来确定题解的表示方式，我们将点的坐标值排在一起组成一个长长的数组。
而解的范围就是坐标域的范围（为了绘制时留出一些空白可以使解的范围比坐标域稍小）。如对于400*400的坐标域，可以按如下方式定义解的域：

//题解范围
public List> Domain =>
    Enumerable.Repeat(0, _people.Count * 2)
        .Select((v, i) => Tuple.Create(10, 370))
        .ToList();

成本函数需要对交叉的连线进行计数。下面是实现的成本函数，其中最主要的算法就是计算两条线是否相交。通过遍历每一对连线最终的得到一个成本总和。

public float CrossCost(List v)
{
    // 将数字序列转换成一个key为person，value为(x,y)的字典
    var loc = _people.Select((p, i) => Tuple.Create(p, i))
        .ToDictionary(t => t.Item1, t => new Point(v[t.Item2*2], v[t.Item2*2 + 1]));
    var total = 0;

    // 遍历每一对连线
    for (int i = 0; i < _links.Count; i++)
    {
        for (int j = i+1; j < _links.Count; j++)
        {
            // 获取坐标位置
            var p1 = loc[_links[i][0]];
            var p2 = loc[_links[i][1]];
            var p3 = loc[_links[j][0]];
            var p4 = loc[_links[j][1]];

            // 强制声明为float
            float den = (p4.Y - p3.Y)*(p2.X - p1.X) -
                      (p4.X - p3.X)*(p2.Y - p1.Y);
            // 如果两线平行，则den==0
            if(den==0) continue;
            // 否则，ua与ub就是两条交叉线的分数值
            var ua = ((p4.X - p3.X)*(p1.Y - p3.Y) -
                      (p4.Y - p3.Y)*(p1.X - p3.X))/den;
            var ub = ((p2.X - p1.X)*(p1.Y - p3.Y) -
                      (p2.Y - p1.Y)*(p1.X - p3.X))/den;
            // 如果两条线的分数值介于0和1之间，则两线彼此相交
            if (ua > 0 && ua < 1 && ub > 0 && ub < 1)
                total += 1;
        }
    }
    return total;
}

这其中用到的Point类：

class Point
{
    public Point(int x, int y)
    {
        X = x;
        Y = y;
    }
    public int X { get; set; }
    public int Y { get; set; }
}

然后我们还需要把得到的结果绘制出来，我们实现名为DrawNetwork的方法通过GDI+来完成图像的绘制。

需要在项目中添加程序集System.Drawing的应用

public void DrawNetwork(List sol)
{
    // 将数字序列转换成一个key为person，value为(x,y)的字典
    var pos = _people.Select((p, i) => Tuple.Create(p, i))
        .ToDictionary(t => t.Item1, t => new Point(sol[t.Item2 * 2], sol[t.Item2 * 2 + 1]));

    Bitmap b = new Bitmap(400,400,PixelFormat.Format24bppRgb);
    using (var g = Graphics.FromImage(b))
    {
        g.Clear(Color.White);
        var pen = new Pen(Color.Black, 1);
        // 绘制连线
        foreach (var l in _links)
        {
            var start = pos[l[0]];
            var end = pos[l[1]];
            g.DrawLine(pen, start.X, start.Y, end.X, end.Y);
        }
        // 绘制字符串
        var font = new Font("Times New Roman", 12);
        var brush  = new SolidBrush(Color.Black);
        foreach (var pkv in pos)
        {
            g.DrawString(pkv.Key,font,brush,pkv.Value.X,pkv.Value.Y);
        }

        b.Save($"result{DateTime.Now.Second}{DateTime.Now.Millisecond}.png", ImageFormat.Png);
    }
}

依然利用前文实现的优化算法来进行测试：

var net = new SocialNetwork();
var traval = new Travel();
var s = traval.RandomOptimize(net.Domain, net.CrossCost);
net.DrawNetwork(s);
s = traval.GeneticOptimize(net.Domain, net.CrossCost);
net.DrawNetwork(s);

在楼主的电脑上GeneticOptimize算法得到的图形如下：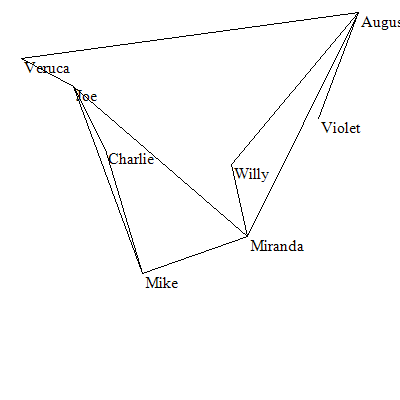

可以看到相交的情况被控制很好，但图形由于边夹角比较小原因并不是很好看。这是因为我们的成本函数并没有给予过小的夹角一定惩罚，可以在成本函数中添加对夹角进行判断的代码来进行优化：

之前的代码中（原书实现方式的代码）在判断相交时将连线两两进行计算，这会白白进行很多无用的计算，在这个优化中，正好可以借夹角判断需要寻找共点线段的机会，将已共点的线段排除在相交判断之外，从而减少运算次数。

public float CrossCost(List v)
{
    // 将数字序列转换成一个key为person，value为(x,y)的字典
    var loc = _people.Select((p, i) => Tuple.Create(p, i))
        .ToDictionary(t => t.Item1, t => new Point(v[t.Item2 * 2], v[t.Item2 * 2 + 1]));
    var total = 0f;

    // 遍历每一对连线
    for (int i = 0; i < _links.Count; i++)
    {
        for (int j = i + 1; j < _links.Count; j++)
        {
            //判断是否共点
            var concurrent = false;
            var radian = 0f;
            if (_links[i][0] == _links[j][0])
            {
                radian = CalcRadian(loc[_links[i][0]], loc[_links[i][1]], loc[_links[j][1]]);
                concurrent = true;
            }
            if (_links[i][1] == _links[j][0])
            {
                if(_links[i][0] == _links[j][1]) continue; //排除共线不同向的线段
                radian = CalcRadian(loc[_links[i][1]], loc[_links[i][0]], loc[_links[j][1]]);
                concurrent = true;
            }
            if (_links[i][0] == _links[j][1])
            {
                radian = CalcRadian(loc[_links[i][0]], loc[_links[i][1]], loc[_links[j][0]]);
                concurrent = true;
            }
            if (_links[i][1] == _links[j][1])
            {
                radian = CalcRadian(loc[_links[i][1]], loc[_links[i][0]], loc[_links[j][0]]);
                concurrent = true;
            }
            if (concurrent)
            {
                //如果角度小于Math.PI/4(22.5度)我们认为是不好看的
                if(radian*4 0 && ua < 1 && ub > 0 && ub < 1)
                total += 1;
        }
    }
    return total;
}

其中用到的计算角度（弧度）的方法是在网上借(piao)鉴(qie)的：

// 计算夹角角度(返回弧度)
private float CalcRadian(Point o, Point s, Point e)
{
    float cosfi = 0, fi = 0, norm = 0;
    float dsx = s.X - o.X;
    float dsy = s.Y - o.Y;
    float dex = e.X - o.X;
    float dey = e.Y - o.Y;

    cosfi = dsx * dex + dsy * dey;
    norm = (dsx * dsx + dsy * dsy) * (dex * dex + dey * dey);
    cosfi /= (float)Math.Sqrt(norm);

    if (cosfi >= 1.0) return 0;
    if (cosfi <= -1.0) return (float)Math.PI;
    fi = (float)Math.Acos(cosfi);

    if (fi < Math.PI)
    {
        return fi;
    }
    return (float)Math.PI * 2 - fi;
}

以上成本函数经过模拟退火算法的优化在楼主电脑上得到图像如下：

var net = new SocialNetwork();
var traval = new Travel();
var s = traval.AnnealingOptimize(net.Domain, net.CrossCost, step:50, cool:0.99f);
net.DrawNetwork(s);

另外一个可以优化的地方就是点之间的距离，将各点之间保持一个适当的距离可以使图看起来更舒展。我们在成本函数CrossCount的最后加上如下代码：

for (var i = 0; i < _people.Count; i++)
{
    for (var j = i + 1; j < _people.Count; j++)
    {
        //获得两点位置
        var p1 = loc[_people[i]];
        var p2 = loc[_people[j]];
        //计算两节点间的距离
        var dist = (float)Math.Sqrt(Math.Pow(p1.X - p2.X, 2) + Math.Pow(p1.Y - p2.Y, 2));
        //对间距小于50个像素的节点进行惩罚
        if (dist < 50)
            total += 1 - dist / 50;
    }
}

这段代码对小于50px的两个点增加一定量的惩罚值，而且距离越小所增加的惩罚会越多。

最终版本的成本函数在模拟退火算法下得到的图像：

每次执行得到的结果基本不可能相同

总结

所有可以利用优化算法解决的问题的要求：问题有一个定义好的成本函数，且相似的解会产生相似的结果。

 

转载于:https://www.cnblogs.com/lsxqw2004/p/6209393.html