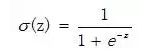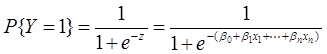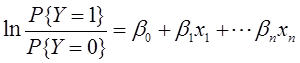回归分析是研究变量之间定量关系的一种统计学方法,具有广泛的应用。
Logistic回归模型
线性回归
先从线性回归模型开始,线性回归是最基本的回归模型,它使用线性函数描述两个变量之间的关系,将连续或离散的自变量映射到连续的实数域。
模型数学形式:
引入损失函数(loss function,也称为错误函数)描述模型拟合程度:
使J(w)最小,求解优化问题得到最佳参数。
Logistic回归
logistic回归(Logistic regression 或 logit regression)有时也被译为"逻辑回归",不过它和"逻辑"并没有太大关系应该只是音译。从内容来讲,它最合适的名字应该是logit回归。
logistic回归模型更多的被用于概率分类器中。线性回归将自变量映射到连续的实数,在很多情况下因变量的取值是在有限的区间中的,最常见的如概率问题的0-1区间。
Sigmod函数提供了一个从实数域到(0,1)的映射:
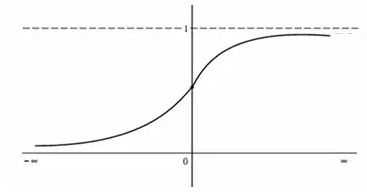
该函数如图:
以数学形式给出把线性模型映射到0-1的方式:
逆变换:
这个变换被称为logit变换,或许就是该模型名字的来源。
logistic回归通常被用做概率分类器,以p=0.5作为分解线。
求解规划模型
最小二乘法
最小二乘法通过数学推导得到全局最优解的表达式,是一种完全数学描述的方法,直接给出求解公式。
最小二乘法可以得到全局最优解,但是因涉及超大矩阵的求逆运算而难以求解。
梯度下降(上升)法:
梯度下降法是一种典型的贪心算法,它从任意一组参数开始,向着使目标函数最小的方向调整参数,直至无法使目标函数继续下降时,停止计算。
多元函数微积分中, 梯度指向函数值变化最快方向的向量. 梯度下降法无法保证的得到全局最优解
梯度下降法有批量梯度下降法和随机梯度下降法两种实现方法。
批量梯度下降(上升)法(Batch Gradient Descent/Ascent)
批量梯度下降法的算法流程:
初始化回归系数为1
重复执行直至收敛 {
计算整个数据集的梯度
按照递推公式更新回归梯度
}
返回最优回归系数值将损失函数J(w)求偏导,得到J(w)的梯度。以矩阵形式给出:
![]()
alpha是下降步长,由迭代公式:
![]()
随机梯度下降(上升)法(stochastic gradient Descent/Ascent)
随机梯度下降法的算法流程:
初始化回归系数为1
重复执行直至收敛 {
对每一个训练样本{
计算样本的梯度
按照递推公式更新回归梯度
}
}
返回最优回归系数值为了加快收敛速度,做出两个改进:
(1)在每次迭代时,调整更新步长alpha的值。随着迭代的进行,alpha越来越小
(2)每次迭代改变样本的顺序,也就是随机选择样本来更新回归系数
Logistic 回归的实现
训练数据testSet.txt,包含m行n+1列:
m行代表m条数据,每条数据前n列代表n个样本,第n+1列代表分类标签(0或1)。
Python:
分类器被封装在类中:
from numpy import *
import matplotlib.pyplot as plt
def sigmoid(X):
return 1.0/(1+exp(-X))
class logRegressClassifier(object):
def __init__(self):
self.dataMat = list()
self.labelMat = list()
self.weights = list()
def loadDataSet(self, filename):
fr = open(filename)
for line in fr.readlines():
lineArr = line.strip().split()
dataLine = [1.0]
for i in lineArr:
dataLine.append(float(i))
label = dataLine.pop() # pop the last column referring to label
self.dataMat.append(dataLine)
self.labelMat.append(int(label))
self.dataMat = mat(self.dataMat)
self.labelMat = mat(self.labelMat).transpose()
def train(self):
self.weights = self.stocGradAscent1()
def batchGradAscent(self):
m,n = shape(self.dataMat)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(self.dataMat * weights) #matrix mult
error = (self.labelMat - h) #vector subtraction
weights += alpha * self.dataMat.transpose() * error #matrix mult
return weights
def stocGradAscent1(self):
m,n = shape(self.dataMat)
alpha = 0.01
weights = ones((n,1)) #initialize to all ones
for i in range(m):
h = sigmoid(sum(self.dataMat[i] * weights))
error = self.labelMat[i] - h
weights += (alpha * error * self.dataMat[i]).transpose()
return weights
def stocGradAscent2(self):
numIter = 2
m,n = shape(self.dataMat)
weights = ones((n,1)) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
h = sigmoid( sum(self.dataMat[randIndex] * weights) )
error = self.labelMat[randIndex] - h
weights += (alpha * error * self.dataMat[randIndex]).transpose()
del(dataIndex[randIndex])
return weights
def classify(self, X):
prob = sigmoid(sum( X * self.weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def test(self):
self.loadDataSet('testData.dat')
weights0 = self.batchGradAscent()
weights1 = self.stocGradAscent1()
weights2 = self.stocGradAscent2()
print('batchGradAscent:', weights0)
print('stocGradAscent0:', weights1)
print('stocGradAscent1:', weights2)
if __name__ == '__main__':
lr = logRegressClassifier()
lr.test()Matlab
上述Python代码用Matlab实现并不难(只是需要拆掉类封装),只是Matlab的广义线性模型工具箱提供了Logistic模型的实现。
trainData = [0 1; -1 0; 2 2; 3 3; -2 -1;-4.5 -4; 2 -1; -1 -3];
group = [1 1 0 0 1 1 0 0]';
testData = [5 2;3 1;-4 -3];
[testNum, attrNum] = size(testData);
testData2 = [ones(testNum,1), testData];
B = glmfit(trainData, [group ones(size(group))],'binomial', 'link', 'logit')
p = 1.0 ./ (1 + exp(- testData2 * B))B = glmfit(X, [Y N],'binomial', 'link', 'logit')
X参数为特征行向量组, Y为代表预先分组的列向量,N是一个与Y同型的向量,Y(i)的在[0 N(i)]范围内取值。
B为[1, x1, x2,...]的系数,测试数据的第一列被加上了1。
p = 1.0 ./ (1 + exp(- testData2 * B))
代入sigmoid函数求解。