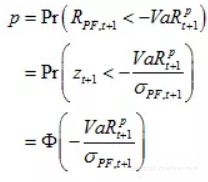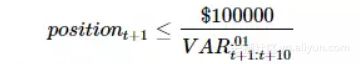【Python金融量化】VaR系列(一):HS,WHS,RM方法估计VaR
最近参加了一个线上学习计划,一群人一起学《Elements of Financial Risk Management》这本书,主要偏向于金融时间序列和多因子模型的知识,结合python编程。现在已经看了三分之一左右,感觉写的还不错,有些收获,意外惊喜是教材的答案全是用excel公式做的,头一次发现excel还可以做极大似然估计这种东西,很神奇。
VaR的估计是书中一个重要部分,从最浅显的HS模型开始不断深入到蒙特卡洛,讨论了若干估计方法,边学习边总结吧。这次主要总结三种不需要考虑分布的方法,并分析每种方法的特点。
VaR定义
这里所说的VaR并非时间序列中的向量自回归模型(vector autoregression),而是在险价值(Value at Risk)。指的是一定概率下,一个金融资产在未来一段时间内的最大可能损失,是对金融资产风险情况的一种度量,数学定义为:
给定置信度p下,VaR为满足下式的值
如果用对数收益率R衡量损失,可以表示为
即也就是说,金融资产的收益率有1-p的概率不会小于-VaR,有p的概率会小于-VaR。如果能准确估计出金融资产未来一段时间内的VaR,对于企业做出投资决策有重要意义。
我们把置信度为p时,第t天起未来k天的在险价值 (100% p VaR for the k-days ahead return)记为![]() ,首先考虑最简单的情况,估计单个股票的
,首先考虑最简单的情况,估计单个股票的![]() 。
。
VaR估计
1. HS方法
根据VaR的定义可以看出,如果我们能得到股票收益率的分布函数,就可以直接算出VaR。最简单的估计方法HS,WHS就从这种考虑出发,但不考虑去估计分布。
HS方法称为历史模拟法(Historical Simulation),HS方法每次取一定长度的历史数据作为样本,将样本的分布看作是整体分布,在置信度p下,只需要找这些历史数据的前p-分位数,认为这些历史数据的p分位数就可以表示VaR。即![]() 如果我们认为取到的历史数据样本确实可以代替整体分布,这种方法是合理的,将收益率序列升序排列后,位于总体100p%处的收益率值,恰好满足VAR定义要求的只有100p%的值小于它,因此可以作为VaR的估计值,如果p分位数位于两个历史数据之间,可以通过插值的方法计算出准确的p分位数。编程实现也很方便,python中的np.percentile函数可以直接得到一列数据的p分位数,excel中也有类似的函数。
如果我们认为取到的历史数据样本确实可以代替整体分布,这种方法是合理的,将收益率序列升序排列后,位于总体100p%处的收益率值,恰好满足VAR定义要求的只有100p%的值小于它,因此可以作为VaR的估计值,如果p分位数位于两个历史数据之间,可以通过插值的方法计算出准确的p分位数。编程实现也很方便,python中的np.percentile函数可以直接得到一列数据的p分位数,excel中也有类似的函数。
• 缺点:准确性低,响应性差,根据后面的例子可以看出。
2.WHS方法
WHS方法(加权历史模拟法)与HS方法的思想类似,不同点在于,HS方法认为过去每天数据包含的的信息量是一样的,WHS认为距离当天越近的数据,对于当天影响更大,应该赋予更高的权重,因此采用加权100p%分位数表示VAR,python中没有直接计算加权分位数的函数,因此需要自己编程实现。根据后面的例子可以看出,WHS效果明显优于HS。
我们分别用两种方法计算S&P500指数多头方和空头方的1-day,1%VAR,数据和Excel过程可以在网站 http://booksite.elsevier.com/9780123744487/ 上找到。
1import os
2os.chdir('F:\\python_study\\python_friday\\July')
3import pandas as pd
4import numpy as np
5from scipy.stats import norm
6from matplotlib import pyplot as plt
7
8# 计算多头和空头的收益率
9data1 = pd.read_excel('Chapter2_data.xls',sheetname = 'Question1_2_forLong')
10data1['return'] = np.log(data1.Close/data1['Close'].shift(1))
11data1['Loss'] = -data1['return']
12data1['VAR'] = np.nan
13
14# HS和WHS
15p = 1
16window = 250
17eta = 0.99
18weights = eta ** (np.arange(250,0,-1) - 1)*(1 - eta)/(1 - eta** window)
19for i in range(window + 1,data1.shape[0]):
20 datause = data1.loc[i - window:i - 1,'return']
21 data1.loc[i,'VAR'] = - np.percentile(datause,p)
22 data1.loc[i,'VAR_WHS'] = np.sort(-datause)[np.min(np.where(weights[np.argsort(-datause)].cumsum()> 0.99))]
23
24# 作图
25data11 = data1.loc[window+1:,:].copy()
26data11 = data11.reset_index(drop = True)
27X = np.arange(data11.shape[0])
28xticklabel = data11.loc[:,'Date'].apply(lambda x:str(x.year) + '-' +str(x.month) + '-' +str(x.day))
29xticks = np.arange(0,data11.shape[0]+1,np.int((data11.shape[0]+1)/4))
30
31plt.figure()
32SP = plt.axes()
33SP.plot(X,data11['Loss'], color = 'red',label = 'Return')
34SP.plot(X,data11.VAR,color = 'black',label = 'VAR(HS)')
35SP.set_xticks(xticks)
36SP.set_xticklabels(xticklabel[xticks])
37plt.xlabel('Loss Date')
38plt.ylabel('HS VaR and Loss')
39plt.grid()
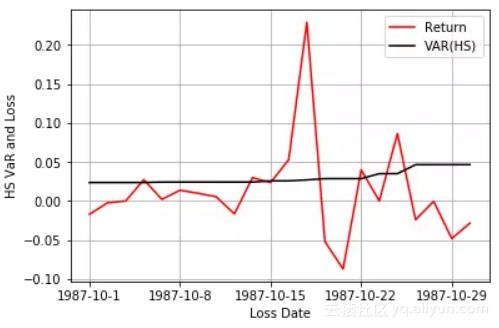
40plt.legend()• HS多头
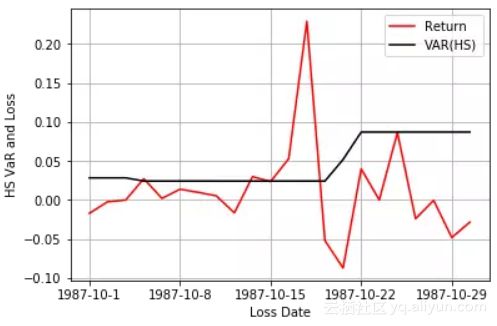
• WHS多头
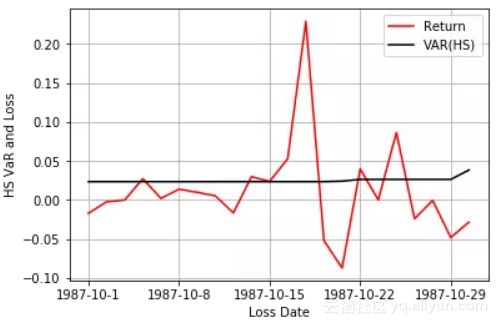
• HS空头
• WHS空头
可以看出,不论是多头还是空头,HS基本上没什么波动,WHS在1987年金融危机时,明显增加。但讲道理两种方法效果都很差,没什么用。但加权分位数的思想还是可以借鉴一下,想了半个多小时才明白是什么意思。
3.RM方法
从之前的分析可以看出,用部分历史数据直接代替总体分布可行性很低,因此还是需要对于总体的分布有一个估计。
RM方法也是比较简单易行的,它假设股票的对数收益率服从正态分布(等价于假设股票价格满足对数正态分布),根据定义,有
其中,![]() 为收益率的标准差, Φ为标准正态分布的分布函数。从而
为收益率的标准差, Φ为标准正态分布的分布函数。从而![]() 等式右侧最后一项为标准正态分布函数反函数在p点处的函数值。
等式右侧最后一项为标准正态分布函数反函数在p点处的函数值。
在这种假设下,要估计VaR,我们只需要对于对数收益率序列的波动率进行建模,估计出未来1天波动率。之后很多方法都是建立在这个框架上。考虑对对数收益率的波动率和分布进行估计。
RM方法是对于波动率的一种简单估计方法,又称风险矩阵法(RiskMetrics),是Garch(1,1)模型的一种特殊情况。认为波动率满足方法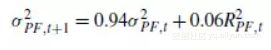 为什么参数用0.94,教材说法是实践证明这种效果最接近现实,后面编程中,波动率的初始值设为0。
为什么参数用0.94,教材说法是实践证明这种效果最接近现实,后面编程中,波动率的初始值设为0。
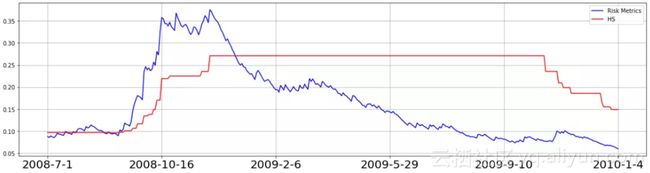
可以看出,RM方法得到的VaR在金融危机时迅速升高,之后逐渐降低,HS就不说了。
1p = 1
2window = 250
3data2['sigma2'] = np.nan
4data2.loc[0,'sigma2'] = 0
5for i in range(data2.shape[0] - 2):
6 data2.loc[i + 1,'sigma2'] = data2.loc[i,'sigma2']*0.94 + 0.06* data2.loc[i,'return']**2
7data2['VAR_RM'] = -data2['sigma2']**0.5 * norm(0,1).ppf(0.01)*np.sqrt(10)
8for i in range(window + 1,data2.shape[0]):
9 data2.loc[i,'VAR_HS'] = - np.percentile(data2.loc[i - window:i - 1,'return'],p)*np.sqrt(10)
10data22 = data2.loc[2019:2374,:].copy()
11data22 = data22.reset_index(drop = True)
12X = np.arange(data22.shape[0])
13xticklabel = data22.loc[:,'Date'].apply(lambda x:str(x.year) + '-' +str(x.month) + '-' +str(x.day))
14xticks = np.arange(0,data22.shape[0]+1,np.int((data22.shape[0]+1)/5))
15
16plt.figure(figsize = [20,5])
17SP = plt.axes()
18SP.plot(X,data22['VAR_RM'],label = 'Risk Metrics',color = 'blue')
19SP.plot(X,data22['VAR_HS'],label = 'HS',color ='red')
20SP.set_xticks(xticks)
21SP.set_xticklabels(xticklabel[xticks],size = 20)
22plt.legend()
23plt.grid()
24plt.show()基于VaR的策略
教材中最后通过VaR设计了一个简单的投资策略,用不同方法下得到的VaR指导投资,把结果进行对比,再次说明RM优于WHS,WHS优于HS。
策略每日都持有指数多头,但仓位根据VaR值确定
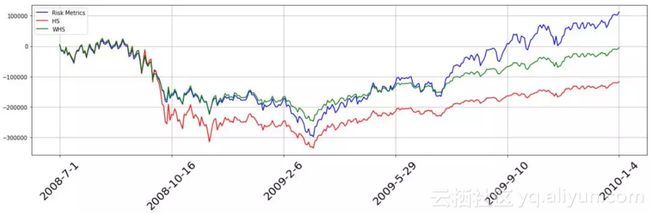
策略在2008年7月1日-2010年1月4日表现如下,三个策略下的净值在金融危机时均迅速下跌,但金融危机过后,RM方法的净值迅速上升,对于风险变化的响应性最好,WHS次之,HS最差。
1p = 1
2window = 250
3eta = 0.99
4weights = eta ** (np.arange(250,0,-1) - 1)*(1 - eta)/(1 - eta** window)
5data2['sigma2'] = np.nan
6data2.loc[0,'sigma2'] = 0
7for i in range(data2.shape[0] - 2):
8 data2.loc[i + 1,'sigma2'] = data2.loc[i,'sigma2']*0.94 + 0.06* data2.loc[i,'return']**2
9data2['VAR_RM'] = -data2['sigma2']**0.5 * norm(0,1).ppf(0.01)*np.sqrt(10)
10for i in range(window + 1,data2.shape[0]):
11 datause = data2.loc[i - window:i - 1,'return']
12 data2.loc[i,'VAR_HS'] = - np.percentile(datause,p)*np.sqrt(10)
13 data2.loc[i,'VAR_WHS'] = np.sort(-datause)[np.min(np.where(weights[np.argsort(-datause)].cumsum()> 0.99))]*np.sqrt(10)
14data2['position_HS'] = 100000/data2['VAR_HS']
15data2['position_WHS'] = 100000/data2['VAR_WHS']
16data2['position_RM'] = 100000/data2['VAR_RM']
17data2['return_HS'] = (np.exp(data2['return']) - 1)*data2['position_HS']
18data2['return_WHS'] = (np.exp(data2['return']) - 1)*data2['position_WHS']
19data2['return_RM'] = (np.exp(data2['return']) - 1)*data2['position_RM']
20
21data22 = data2.loc[2019:2374,:].copy()
22data22 = data22.reset_index(drop = True)
23data22['cum_HS'] = data22['return_HS'].cumsum()
24data22['cum_WHS'] = data22['return_WHS'].cumsum()
25data22['cum_RM'] = data22['return_RM'].cumsum()
26
27X = np.arange(data22.shape[0])
28plt.figure(figsize = [20,5])
29SP = plt.axes()
30SP.plot(X,data22['cum_RM'],label = 'Risk Metrics',color = 'blue')
31SP.plot(X,data22['cum_HS'],label = 'HS',color ='red')
32SP.plot(X,data22['cum_WHS'],label = 'WHS',color ='green')
33xticklabel = data22.loc[:,'Date'].apply(lambda x:str(x.year) + '-' +str(x.month) + '-' +str(x.day))
34SP.set_xticks(xticks)
35SP.set_xticklabels(xticklabel[xticks],rotation=45,size =20)
36plt.legend()
37plt.grid()
38plt.show()
原文发布时间为:2018-08-23
本文作者:hzp
本文来自云栖社区合作伙伴“Python爱好者社区”,了解相关信息可以关注“Python爱好者社区”。