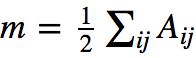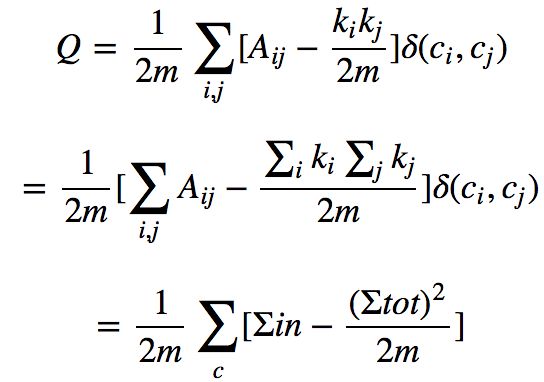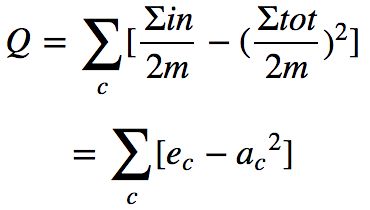1. 社团划分
0x1:社区是什么
在社交网络中,用户相当于每一个点,用户之间通过互相的关注关系构成了整个网络的结构,在这样的网络中,有的用户之间的连接较为紧密,有的用户之间的连接关系较为稀疏,在这样的的网络中,连接较为紧密的部分可以被看成一个社区,其内部的节点之间有较为紧密的连接,而在两个社区间则相对连接较为稀疏,这便称为社团结构。如下图,红色的黑色的点集呈现出社区的结构,
用红色的点和黑色的点对其进行标注,整个网络被划分成了两个部分,其中,这两个部分的内部连接较为紧密,而这两个社区之间的连接则较为稀疏。
如何去划分上述的社区便称为社区划分的问题。
(Newman and Gievan 2004) A community is a subgraph containing nodes which are more densely linked to each other than to the rest of the graph or equivalently, a graph has a community structure if the number of links into any subgraph is higher than the number of links between those subgraphs.
这句话很明确地说明了在什么业务场景下可以使用社区发现算法:
1. 即我们需要先确定要解决的业务场景中,存在明显的聚集规律,节点(可以是抽象的)之间形成一定的族群结构,而不是呈现无规律的随机分散; 2. 同时另一方面,这种聚集的结构是“有意义的”,这里所谓的有意义是指这种聚集本身可以翻译为一定的上层业务场景的表现
0x2:社区划分的出发点和意图
直观地说,community detection的一般目标是要探测网络中的“块”cluster或是“社团”community。
这么做的目的和效果有许多,比如说机房里机器的连接方式,这里形成了网络结构,那么,哪些机器可以视作一个“块”?进一步地,什么样的连接方式才有比较高的稳定性呢?如果我们想要让这组服务瘫痪,选择什么样的目标呢?
我们再看一个例子,word association network。即词的联想/搭配构成的网络:
我们用不同的颜色对community进行标记,可以看到这种detection得到的结果很有意思。
这个网络从词bright开始进行演化,到后面分别形成了4个组:Colors, Light, Astronomy & Intelligence。
可以说以上这4个词可以较好地概括其所在community的特点(有点聚类的感觉);另外,community中心的词,比如color, Sun, Smart也有很好的代表性(自动提取摘要)。
同时我们注意到,那些处在交叠位置的词呢,比如Bright、light等词,他们是同义项比较多的词。这个图也揭示出了这一层含义。
0x3:社区划分的思路概要
什么样的结构能成为团?一种很直观的想法是,同一团内的节点连接更紧密,即具有更大的density。
接下来的问题是,什么样的metrics可以用来描述这种density?Louvian 定义了一个数值上的概念(本质上就是一个目标函数),有了这个目标函数,就可以引出接下来要讨论的 method based on modularity optimization
要注意的,社区划分有很多不同的算法,本文讨论的 Fast Unfolding(Louvian)只是其中一种,而这种所谓的density密度评估方法也其实其中一种思想,不要固话地认为社区划分就只有这一种方法。
Relevant Link:
https://stackoverflow.com/questions/21814235/how-can-modularity-help-in-network-analysis http://iopscience.iop.org/article/10.1088/1742-5468/2008/10/P10008/fulltext/ https://www.researchgate.net/publication/1913681_Fast_Unfolding_of_Communities_in_Large_Networks?enrichId=rgreq-d403e26a5cb211b7053c36946c71acb3-XXX&enrichSource=Y292ZXJQYWdlOzE5MTM2ODE7QVM6MTAxOTUyNjc5NTc5NjY3QDE0MDEzMTg4MjE3ODA%3D&el=1_x_3&_esc=publicationCoverPdf https://www.jianshu.com/p/4ebe42dfa8ec https://blog.csdn.net/u011089523/article/details/79090453 https://blog.csdn.net/google19890102/article/details/48660239 《Fast Unfolding of Communities in Large Networks》
2. LOUVAIN算法模型
0x1:Modularity的定义 - 描述社区内紧密程度的值Q
模块度是评估一个社区网络划分好坏的度量方法,它的物理含义是社区内节点的连边数与随机情况下的边数只差,它的取值范围是 [−1/2,1),其定义如下:
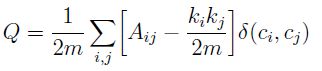
A为邻接矩阵,Aij代表了节点 i 和节点 j 之间 边的权重,网络不是带权图时,所有边的权重可以看做是 1;
![]() 是所有与节点 i 相连的 边的权重之和(度数),kj也是同样;
是所有与节点 i 相连的 边的权重之和(度数),kj也是同样;
![]() 是节点 i 的社区,
是节点 i 的社区,![]() 函数表示若节点 i 和节点 j 在同一个社区内,则返回 1,否则返回 0;
函数表示若节点 i 和节点 j 在同一个社区内,则返回 1,否则返回 0;
模块度的公式定义可以作如下简化:
其中 Σin 表示社区 C 内的边的权重之和,Σtot 表示与社区 C 内的节点相连的边的权重之和。
上面的公式还可以进一步简化成:
这样模块度也可以理解是:
首先modularity是针对一个社区的所有节点进行了累加计算。
modularity Q的计算公式背后体现了这种思想:社区内部边的权重减去所有与社区节点相连的边的权重和,对无向图更好理解,即社区内部边的度数减去社区内节点的总度数。
可以直观去想象一下,如果一个社区节点完全是“封闭的(即所有节点都互相内部连接,但是不和社区外部其他节点有连接,则modularity公式的计算结果为1)”
基于模块度的社区发现算法,都是以最大化模块度Q为目标。可以看到,这种模型可以支持我们通过策略优化,去不断地构造出一个内部聚集,外部稀疏连接的社区结构
在一轮迭代后,若整个 Q 没有变化,则停止迭代,否则继续迭代,直至收敛。
0x2:模块度增量 delta Q
模块增益度是评价本次迭代效果好坏的数值化指标,这是一种启发式的优化过程。类似决策树中的熵增益启发式评价。
ki 代表入射节点 i 的总权重;
在算法的first phase,判断一个节点加入到哪个社区,需要找到一个delta Q最大的节点 i,具体的算法我们后面会详细讨论,这里只需要记住 delta Q的作用类似决策树中的信息增益评估的作用,它帮助整个模型向着Modularity不断增大的方向去靠拢。
3. LOUVAIN算法策略
Louvain算法是基于模块度的社区发现算法,该算法在效率和效果上都表现较好,并且能够发现层次性的社区结构,其优化目标是:最大化整个社区网络的模块度。
即让整个社区网络呈现出一种模块聚集的结构。
0x1:算法思想的联想
1. 两台主机拥有类似的网络对外发包模式
2. 两台主机间拥有累计的event log序列
3. 两个攻击payload拥有类似的词频特征,可以认为是同一组漏洞利用方式 4. 在netword gateway上发现了类似的网络raw流量,也可以反过来用一直的label流量特征进行有监督的聚类 ..
社区发现可能可以提供一种更高层的视角来看待整体的大盘情况,具体的应用场景还需要不断的摸索。
0x2:关于启发式/贪婪思想的社区发现的进一步思考
社区发现算法,或者说在社区发现的项目中,很容易遇到的一个问题就是:“社区过大,将过多的outerlier包括到了社区中”,换句话说,社区聚类的过程中没有能及时收敛。
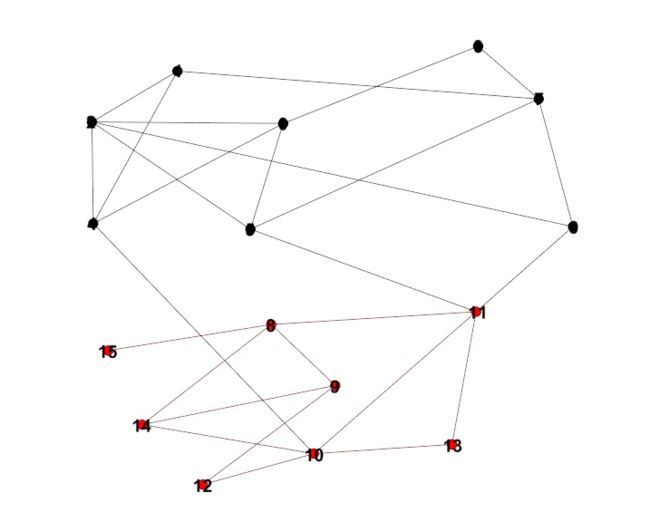
我们来看下面这张图:
如果按照启发式/贪婪思想进行”one-step one node“的社区聚类,O9、O10、O11会被先加入到社区D中,因为在每次这样的迭代中,D社区内部的紧密度(不管基于node密度还是edge得modularity评估)都是不断提高,符合算法的check条件,因此,O9、O10、O11会被加入到社区D中。
随后,O1 ~ O8也会被逐个被加入到社区D中,加入的原因和O9、O10、O11被加入是一样的。
从局部上来看,这些步骤是合理的,但是如果从上帝视角的全局来看,这种做法导致outerlier被错误的聚类到的社区中,导致precision下降。
解决这种问题的一个办法我觉得可以从CNN/DNN的做法中得到灵感,即设置一个Delta增益的阈值,即在每轮的迭代中(社区扩增后紧密度提升的度量)如果不能超过这个阈值,则判定为收敛成功,立即停止算法迭代。
0x3:社区发现(聚类)的效果非常依赖于weight权重计算的策略和方法
louvain社区发现是将一个无向权重图,转化为多个节点集合,每个节点集合代表了一个社区。
社区发现的思想是非常直接简单的,因为聚类的效果非常依赖于weight权重计算的方法,我们选择的权重计算方法必须要能够“很好地”在值域空间中分离开来,否则会导致overcluster。
在实际工程中,我们发现,如果采用exp的【0,1】概率值域空间,节点间weight的区别非常小,很容易导致社区发现算法将全部节点都判定为同一个社区。
1. weight的表征意义问题要特别注意!
weigth对于pylouvain社区发现算法来说,期望表征的是节点间的关系,这种关系必须是非对偶已经唯一确定的。
举例来说,如果我们用节点间的simhash相似性来表征来节点间的weight,则会出现这种情况:
A <-> B:weight(相似性)= 0.1
B <-> C:weight(相似性)= 0.1
但是,很可能存在 A 和 C 是完全不同的两个样本,所以 A 和 C 属于一个社区的这种传递关系是不能成立的。
本质上来说,这涉及到如何进行图节点间weight的特征工程问题,特征工程提取的方法必须要能unique唯一代表样本本身的规律,不能出现:2+8 = 5+5 这种非唯一的情况,即不能出现两个拥有不同概率分布的样本,特征向量是一样的。
4. LOUVAIN算法流程
0x1:算法形式化描述
1)初始化:
将图中的每个节点看成一个独立的社区,社区的数目与节点个数相同;
2)开始first phase迭代 - 社区间节点转移:
对每个节点i,依次尝试把节点 i 分配到其每个邻居节点所在的社区,计算分配前与分配后的模块度变化ΔQ,并记录ΔQ最大的那个邻居节点,如果maxΔQ>0,则把节点 i 分配ΔQ最大的那个邻居节点所在的社区,否则保持不变;
3)重复2)- 继续进行社区间节点转移评估:
直到所有节点的所属社区不再变化,即社区间的节点转移结束,可以理解为本轮迭代的 Local Maximization 已达到;
4)second phase - Rebuilding Graph:
因为在这轮的first phase中,社区 C 中新增了一个新的节点 i,而 i 所在的旧的社区少了一个节点,因此需要对整个图进行一个rebuild。
对图进行重构,将所有在同一个社区的节点重构成一个新社区,社区内节点之间的边的权重更新为新节点的环的权重,社区间的边权重更新为新节点间的边权重;
5)重复2)- 继续开始下一轮的first/second phase:
直到整个图的模块度不再发生变化。
0x2:算法时间复杂度
https://blog.csdn.net/xuanyuansen/article/details/68941507 https://www.cnblogs.com/fengfenggirl/p/louvain.html http://www.cnblogs.com/allanspark/p/4197980.html https://github.com/gephi/gephi/wiki https://blog.csdn.net/qq547276542/article/details/70175157
5. A Python implementation of the Louvain method to find communities in large networks
#!/usr/bin/env python3 # -*- coding: utf-8 -*- ''' Implements the Louvain method. Input: a weighted undirected graph Ouput: a (partition, modularity) pair where modularity is maximum ''' class PyLouvain: ''' Builds a graph from _path. _path: a path to a file containing "node_from node_to" edges (one per line) ''' @classmethod def from_file(cls, path): f = open(path, 'r') lines = f.readlines() f.close() nodes = {} edges = [] for line in lines: n = line.split() if not n: break nodes[n[0]] = 1 nodes[n[1]] = 1 w = 1 if len(n) == 3: w = int(n[2]) edges.append(((n[0], n[1]), w)) # rebuild graph with successive identifiers nodes_, edges_ = in_order(nodes, edges) print("%d nodes, %d edges" % (len(nodes_), len(edges_))) return cls(nodes_, edges_) ''' Builds a graph from _path. _path: a path to a file following the Graph Modeling Language specification ''' @classmethod def from_gml_file(cls, path): f = open(path, 'r') lines = f.readlines() f.close() nodes = {} edges = [] current_edge = (-1, -1, 1) in_edge = 0 for line in lines: words = line.split() if not words: break if words[0] == 'id': nodes[int(words[1])] = 1 elif words[0] == 'source': in_edge = 1 current_edge = (int(words[1]), current_edge[1], current_edge[2]) elif words[0] == 'target' and in_edge: current_edge = (current_edge[0], int(words[1]), current_edge[2]) elif words[0] == 'value' and in_edge: current_edge = (current_edge[0], current_edge[1], int(words[1])) elif words[0] == ']' and in_edge: edges.append(((current_edge[0], current_edge[1]), 1)) current_edge = (-1, -1, 1) in_edge = 0 nodes, edges = in_order(nodes, edges) print("%d nodes, %d edges" % (len(nodes), len(edges))) return cls(nodes, edges) ''' Initializes the method. _nodes: a list of ints _edges: a list of ((int, int), weight) pairs ''' def __init__(self, nodes, edges): self.nodes = nodes self.edges = edges # precompute m (sum of the weights of all links in network) # k_i (sum of the weights of the links incident to node i) self.m = 0 self.k_i = [0 for n in nodes] self.edges_of_node = {} self.w = [0 for n in nodes] for e in edges: self.m += e[1] self.k_i[e[0][0]] += e[1] self.k_i[e[0][1]] += e[1] # there's no self-loop initially # save edges by node if e[0][0] not in self.edges_of_node: self.edges_of_node[e[0][0]] = [e] else: self.edges_of_node[e[0][0]].append(e) if e[0][1] not in self.edges_of_node: self.edges_of_node[e[0][1]] = [e] elif e[0][0] != e[0][1]: self.edges_of_node[e[0][1]].append(e) # access community of a node in O(1) time self.communities = [n for n in nodes] self.actual_partition = [] ''' Applies the Louvain method. ''' def apply_method(self): network = (self.nodes, self.edges) best_partition = [[node] for node in network[0]] best_q = -1 i = 1 while 1: i += 1 partition = self.first_phase(network) q = self.compute_modularity(partition) partition = [c for c in partition if c] # clustering initial nodes with partition if self.actual_partition: actual = [] for p in partition: part = [] for n in p: part.extend(self.actual_partition[n]) actual.append(part) self.actual_partition = actual else: self.actual_partition = partition if q == best_q: # 如果本轮迭代modularity没有改变,则认为收敛,停止 break network = self.second_phase(network, partition) best_partition = partition best_q = q return (self.actual_partition, best_q) ''' Computes the modularity of the current network. _partition: a list of lists of nodes ''' def compute_modularity(self, partition): q = 0 m2 = self.m * 2 for i in range(len(partition)): q += self.s_in[i] / m2 - (self.s_tot[i] / m2) ** 2 return q ''' Computes the modularity gain of having node in community _c. _node: an int _c: an int _k_i_in: the sum of the weights of the links from _node to nodes in _c ''' def compute_modularity_gain(self, node, c, k_i_in): return 2 * k_i_in - self.s_tot[c] * self.k_i[node] / self.m ''' Performs the first phase of the method. _network: a (nodes, edges) pair ''' def first_phase(self, network): # make initial partition best_partition = self.make_initial_partition(network) while 1: improvement = 0 for node in network[0]: node_community = self.communities[node] # default best community is its own best_community = node_community best_gain = 0 # remove _node from its community best_partition[node_community].remove(node) best_shared_links = 0 for e in self.edges_of_node[node]: if e[0][0] == e[0][1]: continue if e[0][0] == node and self.communities[e[0][1]] == node_community or e[0][1] == node and self.communities[e[0][0]] == node_community: best_shared_links += e[1] self.s_in[node_community] -= 2 * (best_shared_links + self.w[node]) self.s_tot[node_community] -= self.k_i[node] self.communities[node] = -1 communities = {} # only consider neighbors of different communities for neighbor in self.get_neighbors(node): community = self.communities[neighbor] if community in communities: continue communities[community] = 1 shared_links = 0 for e in self.edges_of_node[node]: if e[0][0] == e[0][1]: continue if e[0][0] == node and self.communities[e[0][1]] == community or e[0][1] == node and self.communities[e[0][0]] == community: shared_links += e[1] # compute modularity gain obtained by moving _node to the community of _neighbor gain = self.compute_modularity_gain(node, community, shared_links) if gain > best_gain: best_community = community best_gain = gain best_shared_links = shared_links # insert _node into the community maximizing the modularity gain best_partition[best_community].append(node) self.communities[node] = best_community self.s_in[best_community] += 2 * (best_shared_links + self.w[node]) self.s_tot[best_community] += self.k_i[node] if node_community != best_community: improvement = 1 if not improvement: break return best_partition ''' Yields the nodes adjacent to _node. _node: an int ''' def get_neighbors(self, node): for e in self.edges_of_node[node]: if e[0][0] == e[0][1]: # a node is not neighbor with itself continue if e[0][0] == node: yield e[0][1] if e[0][1] == node: yield e[0][0] ''' Builds the initial partition from _network. _network: a (nodes, edges) pair ''' def make_initial_partition(self, network): partition = [[node] for node in network[0]] self.s_in = [0 for node in network[0]] self.s_tot = [self.k_i[node] for node in network[0]] for e in network[1]: if e[0][0] == e[0][1]: # only self-loops self.s_in[e[0][0]] += e[1] self.s_in[e[0][1]] += e[1] return partition ''' Performs the second phase of the method. _network: a (nodes, edges) pair _partition: a list of lists of nodes ''' def second_phase(self, network, partition): nodes_ = [i for i in range(len(partition))] # relabelling communities communities_ = [] d = {} i = 0 for community in self.communities: if community in d: communities_.append(d[community]) else: d[community] = i communities_.append(i) i += 1 self.communities = communities_ # building relabelled edges edges_ = {} for e in network[1]: ci = self.communities[e[0][0]] cj = self.communities[e[0][1]] try: edges_[(ci, cj)] += e[1] except KeyError: edges_[(ci, cj)] = e[1] edges_ = [(k, v) for k, v in edges_.items()] # recomputing k_i vector and storing edges by node self.k_i = [0 for n in nodes_] self.edges_of_node = {} self.w = [0 for n in nodes_] for e in edges_: self.k_i[e[0][0]] += e[1] self.k_i[e[0][1]] += e[1] if e[0][0] == e[0][1]: self.w[e[0][0]] += e[1] if e[0][0] not in self.edges_of_node: self.edges_of_node[e[0][0]] = [e] else: self.edges_of_node[e[0][0]].append(e) if e[0][1] not in self.edges_of_node: self.edges_of_node[e[0][1]] = [e] elif e[0][0] != e[0][1]: self.edges_of_node[e[0][1]].append(e) # resetting communities self.communities = [n for n in nodes_] return (nodes_, edges_) ''' Rebuilds a graph with successive nodes' ids. _nodes: a dict of int _edges: a list of ((int, int), weight) pairs ''' def in_order(nodes, edges): # rebuild graph with successive identifiers nodes = list(nodes.keys()) nodes.sort() i = 0 nodes_ = [] d = {} for n in nodes: nodes_.append(i) d[n] = i i += 1 edges_ = [] for e in edges: edges_.append(((d[e[0][0]], d[e[0][1]]), e[1])) return (nodes_, edges_)
以polbooks.gml为例,16、17、18、19被归类为同一个社区:
node [ id 16 label "Betrayal" value "c" ] node [ id 17 label "Shut Up and Sing" value "c" ] node [ id 18 label "Meant To Be" value "n" ] node [ id 19 label "The Right Man" value "c" ]
从读者的共同购买情况作为权重评估,社区发现的结果暗示了这几本书可能属于同一类的书籍
利用louvain进行社区发现的核心在于,我们需要对我们的业务场景进行抽象,提取出node1_src/node_dst的节点概念,同时要通过专家领域经验,进行节点间weight的计算,得到了weight后,就可以通过louvain这种迭代算法进行社区拓朴的发现了。
Relevant Link:
http://www.cnblogs.com/allanspark/p/4197980.html https://arxiv.org/pdf/0803.0476.pdf https://github.com/LittleHann/pylouvain http://www.cnblogs.com/allanspark/p/4197980.html https://www.jianshu.com/p/e543dc63454f
6. 其他社区发现算法
Relevant Link:
http://blog.sina.com.cn/s/blog_63891e610101722t.html https://www.zhihu.com/question/29042018 https://wenku.baidu.com/view/36fa145a3169a4517623a313.html