Augmenting data structures
Dynamic order statistics
OS-Select(i) - returns ith smallest item in dynamic set
OS-Rank(x) - returns rank of x in sorted order
Idea: Keep subtree sizes in nodes of a red-black tree
OS-Select(x, i) // ith smallest in subtree rooted at x
k ← size[left[x]] + 1 // k = rank(x)
if i = k then return x
if i < k then return OS-Select(left[x], i)
else return OS-Select(right[x], i-k)
Analysis: O(lg n)
OS-Rank in CLRS
OS-Rank(T, x) // rank of x in the tree T
r = x.left.size + 1
y = x
while y ≠ T.root
if y == y.p.right
r = r + y.p.left.size + 1
y = y.p
return r
Q: Why not keep ranks in nodes instead of subtre suzes?
A: Hard to maintain when r-b tree is modified.
Modifying operations: Insert, delete
Strategy: Update subtree sizes when inserting or deleting
Ex: 像一个红黑树insert的时候,不但要重新算size,还要handle rebalancing. recoloring 不影响size。rotation 最多只发生两次,而且只有少量node的size要改变。
Data-Structure augmentation
Methodology (Ex OS trees)
- Choose underlying data structure (red-black tree)
- Determine additional information (subtree size)
- Verity info can be maintained for the modifying operations(Insert, Delete, rotations)
- Develop new operations that use info (DS-Select, OS-Rank)
Usually, mush plays with interactions between steps.
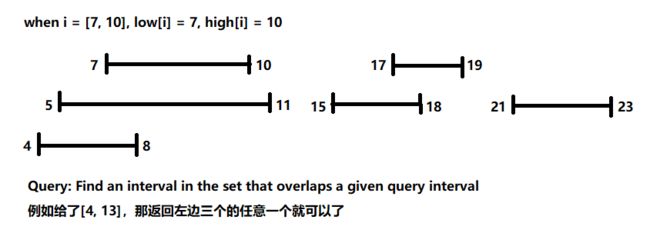
Example: Interval trees
Maintain a set of intervals
e.g. time intervals
Methodology
- red-black tree keyed on the low endpoint (我觉得,同时存了high endpoint)
- Store in the node the largest value m in the subtree rooted at that node
- Modifying ops
Insert: Fix m's on way down
But, also need to handle rotations (takes O(1) time)
Insert time = O(lg n)
Delete similar (书上有但是今晚要自己先想一想) - New opertations
Interval-Search(i) //Find an interval that overlaps i
x ← root
while x ≠ nil and (low[i] > high[int[x]] or low [int[x]] > high[i]) //int[x] = the interval of x
do // i and int[x] don't overlap
if left[x] ≠ nil and low [i] ≤ m[left[x]]
then x ← left[x]
else x ← right[x]
return x
List all overlaps: O(k*lg n) "output sensitive" 方法是每找到一个就把它删掉
Best to date = O(k + lg n) 在另一种数据结构中能实现
k 是overlaps的数量
Correctness
Thearem
Let L = {i' left[x]}, R = {i' right[x]}
- If search goes right then {i' L: i's overlaps i} = ∅
- If search goes left, then:
{i' L: i' overlaps i} = ∅
{i' R: i' overlaps i} = ∅
Proof
Suppose search goes right
- If left[x] = nil, done since L = ∅
- Otherwise, low[i] > m[left[x]]
Suppose search goes left and {i' L : i' overlaps i} = ∅
Then, low[i] m[left[x]] = high[j] for some j L
Since j L, j doesn't overlap i high[i] < low[j]