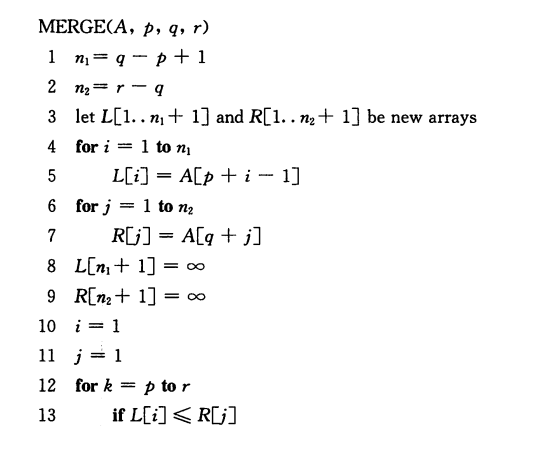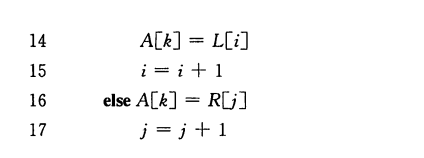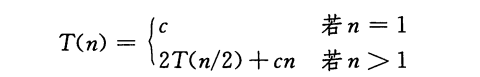《算法导论》的确是本了不起的书,以我现在的水平即使是开头的几章也难以理解透彻,于是就有了”与其问题越堆积越多,不如停下来整理一下所学“这样的念头。
1. 分治
维基百科——
在计算机科学中,分治法是建基于多项分支递归的一种很重要的算法范式。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
维基百科给出了分治法的定义,我相信这比我自己总结的要精确的多,因此直接引用。
分治策略是一种常用的算法策略,它是许多高效算法的基础,其中最耳熟能详的莫过于快速傅里叶变换与归并算法。
在分治策略中,我们递归的求解一个问题,在每层递归中应用下面三个步骤:
- 分解:将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小;
- 解决:递归的求解出子问题,如果子问题的规模够小,停止递归,直接求解。
- 合并:将子问题的解组合成原问题的解。
求解子问题时可能存在两种情况:
- 递归情况:子问题足够大,需要继续递归求解;
- 基本情况:子问题已经足够小,不再需要递归求解,可以直接得出当前子问题的解。
除了这两种与原问题形式相同的子问题情况外,还可能要求求解原问题不一样的子问题,我们将这些子问题的求解看做合并步骤的一部分。
2. 归并算法的例子
我们首先来看看最常见的归并排序算法,关于归并排序的说明实在太多,我相信任何一篇说明该方面的文章都要比我讲述的好,因此在此不再赘述归并排序的详细内容。
简单了解归并排序后,即可发现,归并排序算法完全遵循分治模式,直观上归并排序可以理解为——
- 分解:分解待排序的n个元素的序列成各具n/2个元素的两个子序列;
- 解决:判断问题规模,若是足够小则直接求出答案,若是较大则继续分解问题,递归的求解答案;
- 合并:合并两个已经完成排序的子序列以产生排序的答案。
在归并排序问题中,序列的长度为1时,达到上述的基本情况的要求,不需要做任何工作。因为长度为1的序列必定是有序的。
算法导论中的伪代码如下:
归并排序算法的关键是“合并”步骤中两个已排序序列的合并,这个过程多次调用并且不需要递归,因此我们设计一个辅助过程来实现。应该注意到的是该伪代码设计中使用了“哨兵“,即在数组的最后一个元素后多设一个单元的空间,存放一个特殊值(这里是∞),每当处理到∞ 时即说明该数组的非哨兵元素都已经处理完毕。而∞ 大于任意常量,因此无元素数组不会再被提取元素,后续循环会将未处理完的数组元素一一提取插入新数组。
现在我们将过程MERGE作为一个子程序来调用,若p>=r,则子数组最多有一个元素,所以已经排好序。为了排序整个序列A={ A[1],A[2],.....,A[n] },我们执行初始调用MEAGE-SORT(A,1,A.length),这里A.length=n。
3. 分析归并排序算法
3.1 MERGE
我们首先分析MERGE的时间复杂度,假设第1行到第17行运行一次的代价分别为常量c1,c2....c17,合并后的数组长度为n1+n2=r-p+1=n,可分析得出——
- 第1-3行仅执行一次,代价和为C1+C2+C3;
- 第4,5行执行n1次,第6,7行执行n2次,代价和为n1*(C4+C5)+n2*(C6+C7);
- 第8-11行执行一次,代价和为C8+C9+C10+C11;
- 第12,13行执行n次,14-15行目的为将分数组L的元素逐个插入合数组A中,而L中只有n1个有效元素,因此该部分执行n1次,同理,16-17行执行n2次,代价和为: n*(C12+C13)+n1*(C14+C15)+n2*(C16+C17)。
将以上分析结果累加,常数项合并为CK,得时间复杂度
f(n) = n*(C12+C13)+n1*(C14+C15+C4+C5)+n2*(C16+C17+C6+C7)+CK
=Θ(n)+Θ(n1)+Θ(n2)+Θ(1)
=Θ(n)
3.2 总体
虽然归并排序在元素数并非偶数时仍然能工作,但为了简化分析过程,我们假定问题的规模是2的幂,这时每个分解步骤将产生规模正好为n/2的两个子序列。这个假设将不会影响结果的增长量级。
当有n>1个元素时,设运行时间为T(n),我们分解运行时间为:
- 分解:分解步骤仅仅计算数组的中间位置,需要常量时间,时间复杂度为Θ(1);
- 解决:递归的求解两个规模均为n/2的子问题,将贡献2T(n/2)的运行时间;
- 合并:之前的分析可知在一个具有n个元素的子数组过程上MERGE需要Θ(n)的时间。
由此可得出归并排序最坏情况的运行时间为
当n=1时,T(n) = Θ(1);
当n>1时,T(n)=2T(n/2)+Θ(n)。
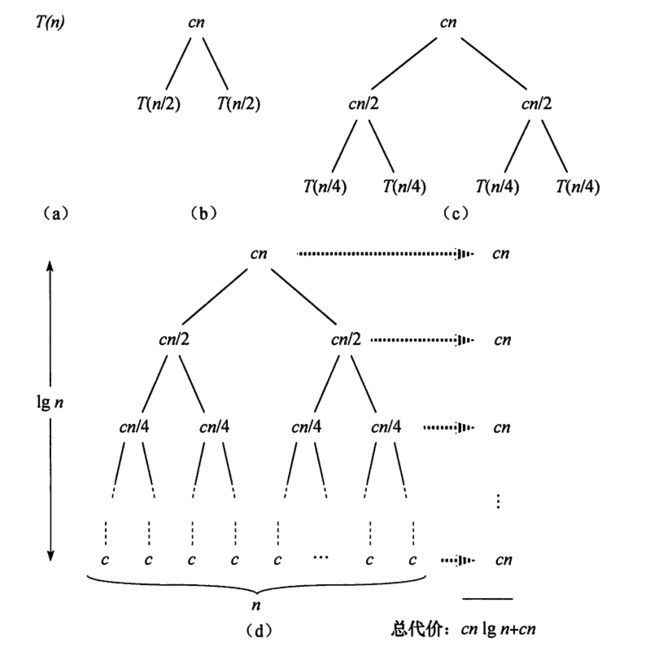
画出递归树
有关递归树的内容之后再详细说明。简而言之,递归树中的每个节点都表示了该节点的代价。T(n)分解之后本身剩余的是合并的代价——Θ(n)=cn,分解后的两个T(n/2)的和是T(n)代价的另一部分,作为cn的两个叶节点,由此可知整棵树中所有节点的代价和即算法的代价。
将T(n)不断分解,直到分解到问题规模为1时,由于n是2的幂,因此需要经过lg(n)层分解。无论如何分解,算法最终都会将各个分数组合并成长度为n的有序数组,每层分解都相当于将长度为n的有序数组不断划分为小数组,即每层操作的数组长度和是不变的,和为n。而合并操作的时间复杂度为Θ(n),因此每层的代价和都为cn。
或者换个严谨些的方式来说,一般来说,若顶层为0层,顶层下的第i层有2^i个节点,每个节点分解解决后合并时需要的代价为其自身的长度,即cn/(2^i)。故每层的代价和为cn,一共有lg(n)+1层,因此整棵树的代价为cn(lg(n)+1)=cn+cn*lg(n)。
忽略低阶项和常量c后就得到了期望的结果Θ(nlg(n))。
4. 递归式
现在我们将上面所说的最坏情况的运行时间写成数学表达式的形式:
这就是递归式了。递归式与分治法是紧密相关的,因为使用递归式可以很自然的刻画分治算法的运行时间。一个递归式就是一个等式或不等式,它通过更小的输入上的函数值来描述一个函数。递归式有很多种形式,例如,算法可能会将问题分解成规模不等的子问题,如2/3和1/3的划分。同时,子问题的规模不必是原问题规模的一个固定比例,例如线性查找的递归式T(n)=T(n-1)+Θ(1)。
《算法导论》介绍了三种求解递归式的方法,即得出算法的”Θ“或”O“渐近界的方法:
- 代入法:我们猜测一个界,然后使用数学归纳法证明这个界的正确性;
- 递归树法:将递归式转换为一棵树,其节点表示不同层次的递归调用产生的代价。然后采用边界和技术来求解递归式;
- 主方法:主方法可用于求解形如 T(n)=aT(n/b)+f(n) 的递归式的界,其中a>=1,b>1,f(n)是一个给定的函数。这种形式的递归式很常见,它描述了一种算法:生成a个子问题,每个子问题的规模是原问题规模的1/b,分解和合并步骤总共花费时间为f(n)。
关于这三种方法的具体情况,我会将它整理在下一篇文章中。
参考文献:Thomas H.Cormen《算法导论》,机械工业出版社, 2006-9-1