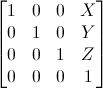2019独角兽企业重金招聘Python工程师标准>>> ![]()
推荐一个学习opengl es非常好的网站,需要:
https://learnopengl.com/Introduction
资料来源:
http://www.learnopengles.com/tag/left-handed-coordinate-system
https://learnopengl.com/Getting-started/Coordinate-Systems
http://www.opengl-tutorial.org/cn/beginners-tutorials/tutorial-3-matrices
http://wiki.jikexueyuan.com/project/modern-opengl-tutorial/tutorial12.html
矩阵
对于opengl es中会大量的用到矩阵,关于矩阵在大学中都是学过的,所以这里做一个简单的记录,主要把忘记的东西重新过一下。
定义
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵
以上来自百度百科
齐次坐标
关于齐次坐标的作用可以查看维基百科,不过更推荐如下篇文章的解释:
下面我要解释的齐次坐标(homogeneous coordinates)是我所熟悉的计算机视觉和图形学这两个领域中经常要用到的概念,同时,坐标也是一般人都可以理解的东西。
二维空间中的一个点是用二元组表示的。我们可以增加一个额外的坐标得到三元组,同时我们声明这是同一个点。这看起来完全无害,因为我们可以很简单地通过增加或者删除最后一个坐标值来在两种表示方式之间来回切换。现在,有一个很重要的问题是:最后一个坐标为什么需要是1?毕竟,另外两个数字没有这样的限制呀。比方说。在这里,我们要再给出一个定义,即当k非零时,所有形如的三元组都表示同一个点,比如和就表示同一个点。由此我们就可以引出齐次坐标的定义,即给定一个二维点,那么形如的所有三元组就都是等价的,它们就是这个点的齐次坐标。对每一个齐次坐标,我们只要把它除以三元组中的第三个数,即可得到原始的二维点坐标(这就是@祝文祥的答案中所说的同比收缩的一个例子)。不过我觉得,从字面上来看,齐次坐标这个叫法还是不那么形象,不过看看和齐次对应的英文单词homogeneous,我们会发现这个词有时还会被翻译成“同质”,表示某一类东西拥有一些相同的性质,这么来看的话,还是挺形象的吧。
需要再次注意的是这里的k是非零的,那么如果会怎样?因为除数不能为的缘故,所以似乎没有任何二维点是和对应的。事实上,就是无穷远处的点。以前,我们用是无法描述二维平面上的无穷远点,但当我们引入齐次坐标之后,就可以用来表示无穷远点了。这就是引入齐次坐标的一个好处。当然了,使用齐次坐标还有很多好处。事实上,没很多好处,我们干嘛要多用一个数字来表示二维点呀,多麻烦你说是吧。
from: https://www.cnblogs.com/sddai/p/5936451.html
齐次坐标的意义可以让我们把二维坐标中的点在三维坐标中得以体现。
矩阵的变换
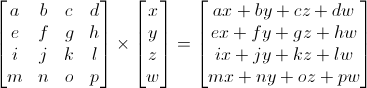
三维图形学中我们只用到4x4矩阵,它能对顶点(x,y,z,w)作变换。这一变换是用矩阵左乘顶点来实现的:
矩阵x顶点(记住顺序!!矩阵左乘顶点,顶点用列向量表示)= 变换后的顶点
这看上去复杂,实则不然。左手指着a,右手指着x,得到ax。 左手移向右边一个数b,右手移向下一个数y,得到by。依次类推,得到cz、dw。最后求和ax + by + cz + dw,就得到了新的x!每一行都这么算下去,就得到了新的(x, y, z, w)向量。
平移矩阵
x,y,z是点的位移增量,如果想把点(a,b,c,1)向x轴移动10个位置则上述的矩阵需要写成:
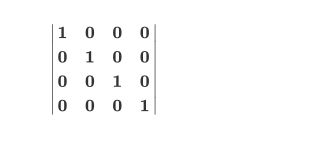
单位矩阵
单位矩阵跟代数计算中的1是一个作用,我们使用任何数乘以1都得到原来的数,单位矩阵同理:
缩放矩阵
旋转矩阵
旋转矩阵比较复杂。这里略过细节,等需要时候再查阅吧。
累计变换
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
** 注意 ** ,这里的代码执行顺序是首先执行缩放,接着旋转,最后才是平移。这是矩阵乘法对应的执行方式。
opengl es 坐标
在opengl es中,总共会有五种的坐标系统,如下所示:
- Local space (or Object space):本地坐标系,即模型本身的坐标系
- World space:世界坐标系
- View space (or Eye space):视图坐标系
- Clip space:裁剪坐标系
- Screen space:屏幕坐标系
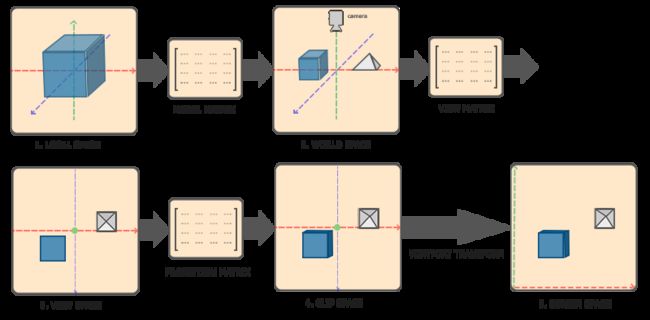
下图展示了如何从本地坐标系经过一系列的矩阵变换(模型矩阵model matrix,视图矩阵view matrix,投影矩阵projetion matrix等),转换到了屏幕坐标系的过程。
- 首先从本地坐标系开始,表示一个模型当前开始的坐标。
- 通过模型矩阵将本地坐标转换到世界坐标当中,世界坐标可以包含很多的模型。
- 在世界坐标中通过视图转换转换到视图坐标中,视图坐标可以理解成我们从相机中看到的视角。
- 在视图坐标中通过投影变换(orthographic projection matrix[正交投影矩阵] or a perspective projection matrix[透视投影矩阵])转换到裁剪坐标当中,裁剪坐标的区间在于[-1.0,1.0]。
- 最后将裁剪坐标转换到屏幕坐标中,这一步通过
glViewport()方法进行。
如何理解这些坐标系呢?
- 首先,本地坐标系很好理解,每个模型都是一个坐标系,中心点位于(0,0,0)点。
- 对于世界坐标系而言,假设不用世界坐标系,则如何把模型集合到一起呢?例如要在客户端展示两个不同位置立方体,所以才提出了世界坐标系的概念。通过模型矩阵(旋转,平移,放大或者缩小),我们可以很容易把模型展示在不同的位置的世界坐标系上面。
- 对于视图坐标系(known as camera space or eye space)而言,就是通过摄像机视角观察的坐标系,由世界坐标系通过视图矩阵转换而来。
- 裁剪坐标系的意义在于裁剪掉超出可观察范围的视图,通过投影变换,转换成NDC(规范化设备坐标)。最终裁剪坐标系会调用
glViewport()转换成设备坐标系完成显示。
投影矩阵介绍
在从视图坐标系转换到裁剪坐标系时候,会通过投影矩阵转化,投影矩阵的主要作用就是将三维降成二维,以便显示在屏幕上。投影矩阵分为两种,一种是正交投影矩阵和透视投影矩阵。
关于两种投影矩阵,不懂得请自行Google吧~