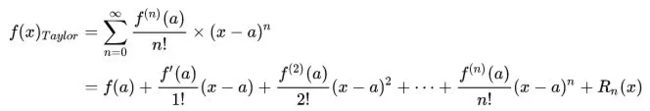先来回顾一下梯度下降法的参数更新公式：
（其中，α是学习速率，
是梯度）
这个公式是怎么来的呢？下面进行推导：
首先，如果一个函数 n 阶可导，那么我们可以用多项式仿造一个相似的函数，这就是泰勒展开式。其在a点处的表达式如下：
可以看出，随着式子的展开，这个展开式越来越接近于原函数。
如果用一阶泰勒展开式，得到的函数近似表达式就是：
。想像梯度下降就是站在山坡上往下走，
是原点，
是往下走一步后所处的点。
我们知道梯度下降每走一步都是朝着最快下山的方向，因此应该最小化
。
我们使用一个向量来表示
：，
也是一个向量，那么上式可写成：
。
既然我们要使
最小，那么只有当
等于-1，也就是
和这两个向量反方向时，才会最小。
当和反方向时，我们可以用向量来表示：
。（其中
表示长度大小）
因为：，代入可得：
。
这样就可以得到参数更新公式：。（其中是步长，是函数在
时的梯度）
因为我们使用的是一阶泰勒展开式，因此
要非常小，式子才成立。也就是说学习速率要非常小才行。所以如果你要让你的损失函数越来越小的话，梯度下降的学习速率就要非常小。如果学习速率没有设好，有可能更新参数的时候，函数近似表达式是不成立的，这样就会导致损失函数没有越变越小。