红黑树
网络上有很多关于红黑树的详细介绍,推荐参考《算法导论》中红黑树一章,讲解的最为清晰和准确。下面我将结合《算法导论》的红黑树介绍与Java8 HashMap红黑树实现,抽取重点信息,尽可能简单的把红黑树的要点介绍出来,许多细节不进行详细说明,如果全部写出来估计与书也差不多。不再赘述,鼓励参阅《算法导论》与Java8 HashMap源代码。
红黑树介绍
红黑树性质(重点):
- 每个结点或是红色的,或是黑色的。
- 根结点是黑色的。
- 每个叶子结点是黑色的。
- 如果一个结点是红色的,则它的两个子结点都是黑色的。
- 对每个结点,从该结点到其所有后代叶子结点的简单路径上,均包含有相同数目的黑色结点。
红黑树的黑高:
从某结点x出发(不包含该结点)到达一个叶子结点任意一条简单路径上的黑色结点个数称为该结点的黑高(black-height)。
红黑树旋转
一种能保证二叉搜索树性质的搜索树局部操作,分为左旋(left rotate)和右旋(right rotate)。
如下图摘自《算法导论》,展示左旋和右旋的操作。
红黑树插入
插入过程
简单分成3步:
- 确定插入位置,新结点作为叶子结点,按照二叉搜索树的性质向下循环寻找结点将要插入的位置。
- 标色,新结点标记为红色。
- 修复红黑树性质。
如何修复红黑树性质
首先,分析在叶子结点处添加一个红结点,可能破坏那些红黑树性质。如下所示,如果插入的结点是根结点,破坏了性质2;如果插入结点的父结点为红色,则破坏了性质4。
1.每个结点或是红色的,或是黑色的。√
2.根结点是黑色的。×
3.每个叶子结点是黑色的。√
4.如果一个结点是红色的,则它的两个子结点都是黑色的。×
5.对每个结点,从该结点到其所有后代叶子结点的简单路径上,均包含有相同数目的黑色结点。√
其次,如果插入的结点是根结点,将结点颜色设置为黑色即可。
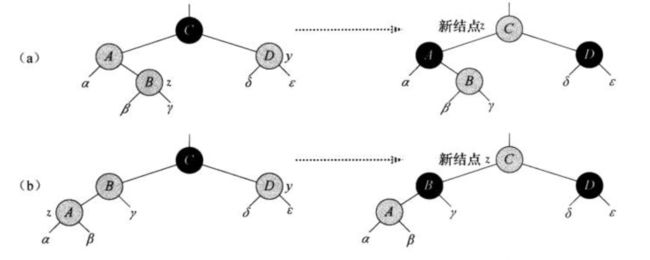
次之,如果破坏了性质4,会分成如下3中情况解决,假设插入的结点为z,并且z的父结点是其祖父结点的左孩子(如果是右孩子操作与左孩子相反)。
-
情况1:z的叔结点y是红色。
操作方法:父结点和叔结点着黑色,祖父结点着红色,z结点上移到祖父结点,循环继续遍历。
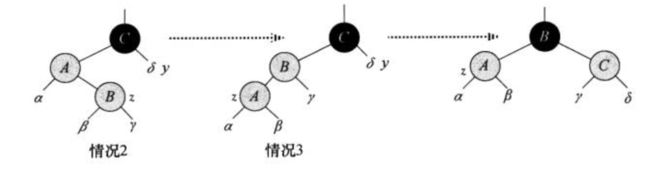
- 情况2:z的叔结点y是黑色的且z是一个右孩子
操作方法:z的父结点左旋变成情况3 -
情况3:z的叔结点y是黑色的且z是一个左孩子
操作方法:z的父结点着黑色,祖父结点着红色,z的祖父结点右旋,结束调整。
红黑树删除
假设将要删除的结点为z,实际删除的结点为y,初始时y=z,进行红黑树性质修复的结点为x。
删除结点z,寻找需要修复的结点x
红黑树的删除操作比插入更复杂一些
- 找到替换z的结点y
- 如果z左子树为null,z的右孩子zr不为null,移到z位置上,x=zr,记录y.color=z.color
- 如果z右子树为null,z的左孩子zl不为null,移到z位置上,x=zl,记录y.color=z.color
- z左右子树均不为null,存在后继结点,y设置为z的中序遍历的后继结点,记录后继结点y的y.color,x=y.right,y替换z,z的颜色复制给y。
- z左右子树均为null,x=null,记录y.color=z.color
- 此时,y.color是实际删除结点的颜色,也就是这个颜色可能破坏了红黑树的性质。
- x指向需要调整的结点。
删除结点可能破坏的性质
- 实际删除结点y的颜色y.color如果是红色不会破坏红黑树性质。
- y的颜色y.color是黑色破坏红黑树性质。
- 如果y是原来的根结点,而y的一个红孩子成为新的根结点,违反了性质2;
- x和x.p是红色的,违反了性质4;
- 在树中移动y导致先前包含y的任何简单路径上黑结点个数少1,违反性质5。
x结点的颜色
如果y是黑色,而x结点可能有三种情况,null,RED和BLACK。为了保证红黑树性质,将x结点视为还有一重额外的黑色,这样任意包含x的路径黑结点个数加1。这样旧解决了上面提到的可能破坏的性质。但是因为此时x结点包含两种颜色,违反了性质1。x结点可能的情况是,null和BLACK、RED和BLACK、BLACK和BLACK。
恢复红黑树性质
x是双重颜色状态
目的将额外的黑色沿树上移,直到
- x指向红黑结点,将x着色为(单个)黑色
- x指向根结点,此时可以简单的移除额外的黑色
- 执行适当的旋转和重新着色
结束程序
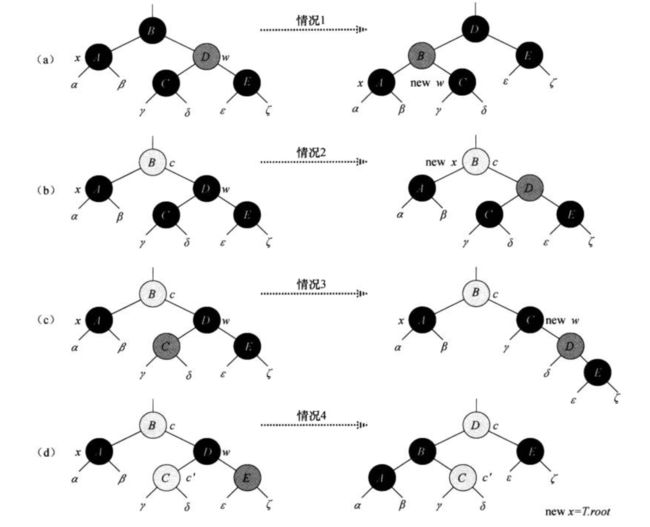
x结点操作可能情况
- 情况1:x的兄弟结点w是红色
操作方法:设x.p是x的父结点。改变w和x.p的颜色,然后对x.p做一次左旋。转换为情况2、情况3或情况4处理。 - 情况2:x的兄弟结点w是黑色的,而且w的两个子结点都是黑色的
操作方法:设x.p是x的父结点。x和w去掉一重黑色,x.p上补偿一重黑色。x上移。 - 情况3:x的兄弟结点w是黑色的,w的左孩子是红色的,w的右孩子是黑色的
操作方法:交换w和其左孩子w.left的颜色,然后对w进行右旋。转换为情况4。 -
情况4:x的兄弟结点w是黑色的,且w的右孩子是红色的
操作方法:重新着色和对xp做一次左旋。符合红黑树性质,结束程序。
如图所示:
HashMap红黑树源码
源码实现的每条语句不详细注释,根据前文所述的内容,在代码处只标示每段执行的含义,并且会做一些简化处理,仅粘贴重要的代码。例如某几条语句标注,执行情况3;标注左旋操作,但是不对左旋操作的代码详细标注。有兴趣的同学可以在纸上按照代码画一画,看看各个指针如何转换的,理解起来就会非常容易。
树化函数
final void treeifyBin(Node[] tab, int hash) {
......
TreeNode hd = null;
do {
TreeNode p = replacementTreeNode(e, null);//生成红黑树结点
......
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);//桶的头节点,调用TreeNode结构的树化函数treeify()
}
/*链表结构转换为红黑树结构*/
final void treeify(Node[] tab) {
TreeNode root = null;//定义根结点
for (TreeNode x = this, next; x != null; x = next) {
next = (TreeNode)x.next;
x.left = x.right = null;
/*设置链表的第一个结点为树根*/
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
/*循环查找插入的位置,代码有删减*/
for (TreeNode p = root;;) {
/*先比较hash值大小*/
/*如果上一步相等,再比较Comparable接口的compareTo*/
/*如果上一步相等或者无法比较,最后调用System.identityHashCode()函数比较*/
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null && (kc = comparableClassFor(k)) == null)
|| (dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
......
root = balanceInsertion(root, x);//插入新结点
}
}
}
}
红黑树插入函数
static TreeNode balanceInsertion(TreeNode root, TreeNode x) {
/*新结点标记为红色*/
x.red = true;
for (TreeNode xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {//根结点处理
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)//x的父结点为黑色
return root;
/*x的父结点为祖父结点的左孩子*/
if (xp == (xppl = xpp.left)) {
/*情况1:x的叔结点y是红色*/
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
/*情况2:x的叔结点y是黑色的且x是一个右孩子*/
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
/*情况3:x的叔结点y是黑色的且x是一个左孩子*/
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {/*x的父结点为祖父结点的右孩子,操作对称相反,此处省略*/}
}
}
红黑树删除函数
static TreeNode balanceDeletion(TreeNode root, TreeNode x) {
for (TreeNode xp, xpl, xpr;;) {
if (x == null || x == root)/*x初始为null或者是根结点*/
return root;
else if ((xp = x.parent) == null) {/*上移之后x为根结点*/
x.red = false;
return x;
}
else if (x.red) {/*x指向红黑结点,将x着色为黑色*/
x.red = false;
return root;
}
/*x为父结点的左孩子*/
else if ((xpl = xp.left) == x) {
/*情况1:x的兄弟结点w是红色*/
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
/*x的兄弟结点w是黑色*/
if (xpr == null)/*x的兄弟结点w为null,直接上移*/
x = xp;
else {
TreeNode sl = xpr.left, sr = xpr.right;
/*情况2:x的兄弟结点w是黑色的,而且w的两个子结点都是黑色的*/
if ((sr == null || !sr.red) && (sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
/*情况3:x的兄弟结点w是黑色的,w的左孩子是红色的,w的右孩子是黑色的*/
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ? null : xp.right;
}
/*情况4:x的兄弟结点w是黑色的,且w的右孩子是红色的*/
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { /*x为父结点的右孩子,代码省略*/}
}
}
总结
Java8 HashMap的红黑树编程用的就是《算法导论》中介绍的红黑树经典算法。许多人可能在学习算法的时候红黑树都没有看懂,也有许多人看懂了《算法导论》中的红黑树算法却从来没有写代码实现过,那么《算法导论》的红黑树一章与Java8 HashMap就是一套最好的理论与实践的结合,具体说是Java的实践。