一、R代码实现。
用google在网上搜索到的回测语句都大同小异,下面给出一个示例,改编自:量化策略回测:
# 以S&P500为例,其雅虎代码为^GSPC;我们要计算5日均线指标的函数就是SMA(),
# 先载入需要的扩展包
> library(quantmod)
> library(PerformanceAnalytics)
# 先获取S&P500的交易数据,然后根据其收盘价(由函数Cl()抽取)计算其5日均线值:
> getSymbols('^GSPC') #S&P500 OHLC data
> close <- Cl(GSPC)
> mv5 <- SMA(close, 5)
# 策略是当收盘价大于5日均线,代表可以入市,取1,否则代表清仓,取0。(-1是代表卖空,不适用。)
> sig <- ifelse(close < mv5, 1, 0)
# 使用Lag()将信号序列向“过去”推迟一天,代表将昨天的信号,应用到今天。
> sig <- Lag(sig) #将该序列向“过去”延迟一天
# 计算收益序列
# discrete代表用离散方式计算当天收益率,即(Close-Close(-1))/Close(-1)
# continous代表用连续方式计算当天收益率,即ln(Close/Close(-1))
> roc <- ROC(type='discrete',close)
> ret <- roc * sig
# 画出策略收益图
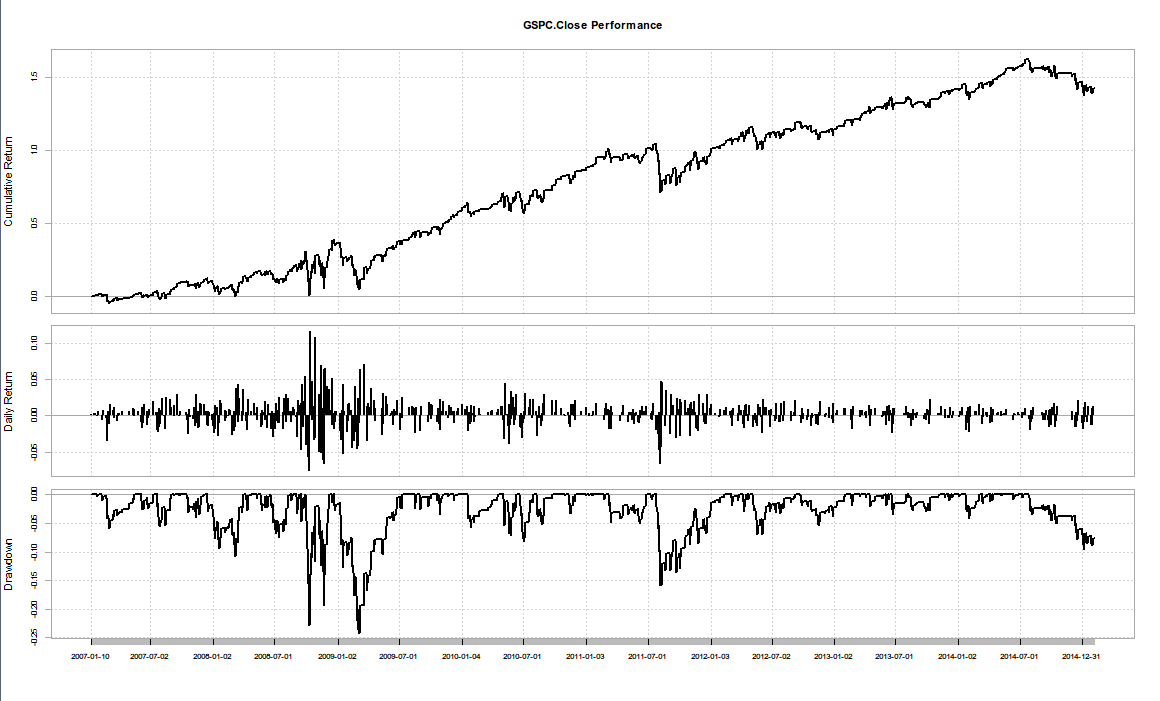
> charts.PerformanceSummary(ret)
# 最上面的板块是积累收益,相当于对cumprod(1+ret)的绘图;
# 第二个是日收益,相当于对ret原始收益数据的绘图;
# 最下面的是下跌图(又称“水下图”),将下跌成分独立绘出,有助于我们分析亏损状况和研究弥补措施。
以上需要注意的地方是制定策略的语句
> sig <- ifelse(close < mv5, 1, 0)
# 当收盘价大于5日均线时,sig取1,否则取0。
在网上公布的代码当中,有的是取-1,这里-1代表卖空,不是清仓,得到的结果是不对的。
二、excel模拟。
当初得到这个结果的时候我很怀疑,用几条R语句就把量化策略及结果模拟出来了?看上去这么神奇,结果对不对呢?我在excel里对该策略进行模拟:
以上面的策略为基础,细化得到的交易方案是这样的:
- 当股票收盘价格高于五日均线,且无持仓,那么第二天满仓入市。
- 当股票收盘价格高于五日均线,且满仓,那么第二天继续持仓。
- 当股票收盘价格低于五日均线,且无持仓,那么第二天继续空仓。
- 当股票收盘价格低于五日均线,且满仓,那么第二天全部平仓。
为了简化计算,假设以前一天的收盘价作为成交价:即以前一天的收盘价满仓入市,或以前一天的收盘价全部平仓。当然这可以在进一步的研究中细化,但这里我们只是为了演示,就不过于复杂了。
excel表格里得到的结果如下:
| CLOSE | SMA | sig | ROC | ROC*sig | 股票 | 现金 | 总收益 | |
|---|---|---|---|---|---|---|---|---|
| 1994-1-3 | 5.6 | 0 | 1 | 1 | ||||
| 1994-1-4 | 5.55 | 0 | 1 | 1 | ||||
| 1994-1-5 | 5.65 | 0 | 1 | 1 | ||||
| 1994-1-6 | 6.1 | 0 | 1 | 1 | ||||
| 1994-1-7 | 6.25 | 5.83 | 0 | 1 | 1 | |||
| 1994-1-10 | 6.45 | 6 | 1 | 0.032 | 0.032 | 1.032 | 0 | 1.032 |
| 1994-1-11 | 6.15 | 6.12 | 1 | -0.047 | -0.047 | 0.984 | 0 | 0.984 |
| 1994-1-12 | 6.15 | 6.22 | 1 | 0 | 0 | 0.984 | 0 | 0.984 |
| 1994-1-13 | 6.25 | 6.25 | 0 | 0.016 | 0 | 0 | 0.984 | 0.984 |
| 1994-1-14 | 6.1 | 6.22 | 0 | -0.024 | 0 | 0 | 0.984 | 0.984 |
| 1994-1-17 | 6 | 6.13 | 0 | -0.016 | 0 | 0 | 0.984 | 0.984 |
| 1994-1-18 | 6.2 | 6.14 | 0 | 0.033 | 0 | 0 | 0.984 | 0.984 |
| 1994-1-19 | 6 | 6.11 | 1 | -0.032 | -0.032 | 0.952 | 0 | 0.952 |
| 1994-1-20 | 6 | 6.06 | 0 | 0 | 0 | 0 | 0.952 | 0.952 |
由于是取5日平均,所以5日平均值SMA从第5个交易日开始出现。这几天的资产都是现金,总收益为1。
从第6个交易日开始,通过判断收盘价与5日均线之间的大小,得到交易信号sig,注意,这里的sig是滞后一日的,代表前一天的收盘价与5日均线之间的相对大小。
1994-1-10 close>SMA,sig=1,以前一天的收盘价6.25满仓入市,当天收盘价为6.45,日内收益率为0.032,股票价值1.032,现金为0,总资产价值为1.032。
1994-1-11 close>SMA,sig=1,鉴于前一天已入市,继续持仓,当天收盘价为6.15,日内收益率为-0.047,股票价值0.984,现金为0,总资产价值为0.984。
1994-1-12 close>SMA,sig=1,继续持仓,当天收盘价为6.15,日内收益率为0,股票价值0.984,现金为0,总资产价值为0.984。
1994-1-13 close
此时,经历了一次持仓以及清仓之后,投资者手里只拥有现金资产,总资产价值为0.984,亏损0.016。
通过对比excel计算的ret(ROC*sig)与R代码计算的ret,两者的结果完全一致。
通过用excel对以上回测策略的模拟,可以发现以上回测策略的隐含前提:
(1) 入市价格和清仓价格均为前一天的收盘价。
(2) 入市则全部满仓,离市则全部清仓。
三、神秘的charts.PerformanceSummary()函数。
在R代码中,一条charts.PerformanceSummary()语句,画出在该策略下,对应股票的总资产收益,日收益和下跌图。它就像一个神奇的黑箱,给我们以策略是否有效以最直观的图形表示。但光有图形还不够,这三条曲线分别对应哪些数据,能不能分别导出方便进一步研究呢?
-
总资产收益。
对应的是excle表格当中的总收益,直观表示了应用该策略,投资者总资产在回测时间内的增减情况。虽然在excel模拟中用股票、现金、总资产三个条目来代表,但其实用一条R代码就可以实现了:
cumprod(1+ret)也就是对(1+ret)的连乘。很容易理解:假设到了第n天,那么这一天的总收益Rn应该等于前一天的总收益R(n-1)乘以当天的收益率,不是ret,而应当是(1+ret)。
R代码得到的结果与excel是一致的。
-
日收益。
就是R代码当中的ret和excel表格中的ROC*sig。
-
下跌图(这部分参考了R包计算回撤)。
这里只是将下跌成分独立绘出,对应的excel数据也是ROC*sig,但这里的下跌图经过了整理。对应的R函数有:
a)chart.Drawdown:下跌图,也就是charts.PerformanceSummary()的第三张图。
data(edhec) chart.Drawdown(edhec[,c(1,2)], main="Drawdown from Peak Equity Attained", legend.loc="bottomleft")b)findDrawdowns:返回回撤的起始时间,时间间隔,回撤数值,常与sortDrawdowns连用找最大回撤。
data(edhec) findDrawdowns(edhec[,"Funds of Funds", drop=FALSE]) sortDrawdowns(findDrawdowns(edhec[,"Funds of Funds", drop=FALSE]))c)maxDrawdown:返回收益时间序列的最大回撤。
data(edhec) t(round(maxDrawdown(edhec[,"Funds of Funds"]),4))d)table.Drawdowns:返回最差回撤的统计量表格。
data(edhec) table.Drawdowns(edhec[,1,drop=FALSE])