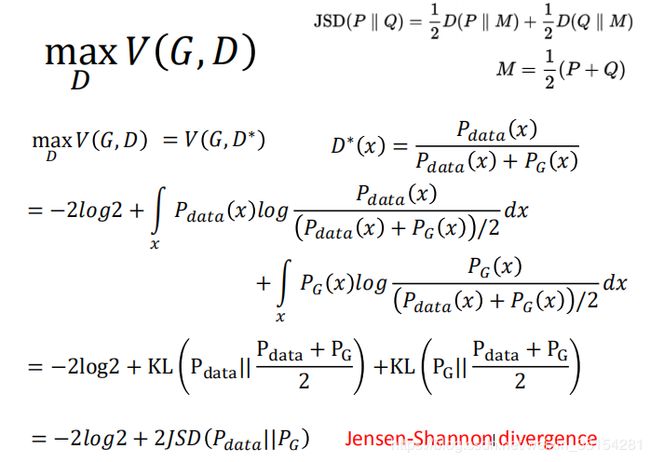Pytorch实现GAN 生成动漫头像

什么是GAN?

​ 　　生成式对抗网络（GAN, Generative Adversarial Networks ）是一种深度学习模型，是近年来复杂分布上无监督学习]最具前景的方法之一。GAN的核心思想来源于博弈论的纳什均衡，它设定参与游戏双方分别为一个生成器和一个判别器，生成器的目的是尽量去学习真实的数据分布，而判别器的目的是尽量正确判别输入数据是来自真实数据还是来自生成器：为了取得预习的胜利，这两个游戏参与者需要不断地优化，各自提高自己的生成能力和判别能力，这个学习优化过程就是寻找二者之间的一个纳什均衡．

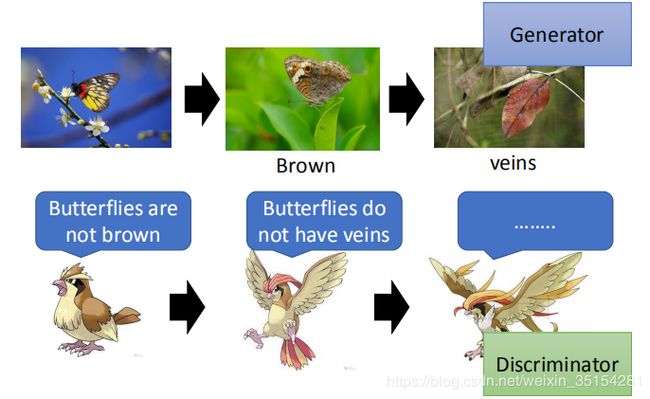
​ 　　上图是枯叶蝶和啵啵鸟的之间相互博弈进化的过程，我们可以把啵啵鸟当做判别器，把蝴蝶当做生成器．在刚开始进化的时候，啵啵鸟认为蝴蝶不是棕色的，而蝴蝶经过几代的进化使得自身的颜色变成棕色来逃避啵啵鸟的猎食，此时的波波鸟也在不断进化，此时它认为蝴蝶是没有翅纹．蝴蝶得到相应的信息，在接下来的几代里不断进化，最后，变成了枯叶蝶，而啵啵鸟也会不断跟进，来猎食枯叶蝶．这种对抗的思想使得蝴蝶尽可能的伪装来骗过啵啵鸟的捕食，啵啵鸟也要能够很好的判别蝴蝶真伪来获取食物，这也很生动的解释了ＧＡＮ对抗的思想．

怎么生成动漫头像？

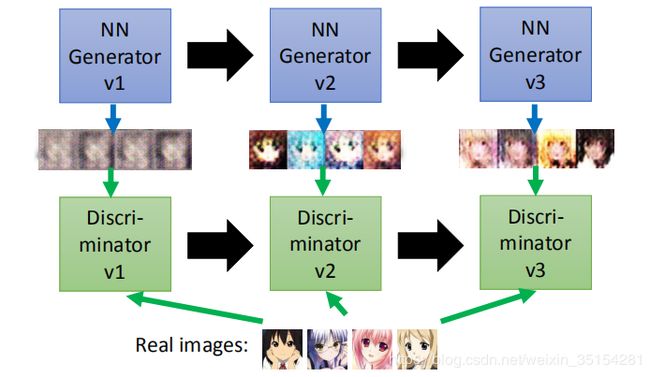
​ 　　在真实的ＧＡＮ生成动漫头像的实现过程中，如下图，我们在第一代的Generator中，通过神经网络生成一张图片，把它送入第一代的Discriminator中，此时第一代的Discriminator也要接受真实图片数据，并且对二者作出评判，我们希望Discriminator能够给给好的动漫头像给高分，不好的动漫头像给低分．接着，第一代Discriminator和Generator相互对抗学习，形成第二代Discriminator和Generator，继续重复操作．直到我们的Generator生成的动漫头像能够使得Discriminator给他很高的分数．

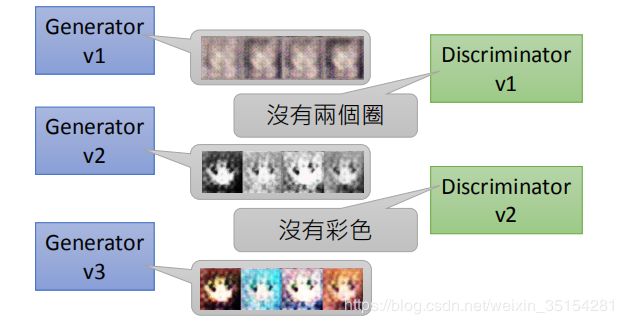
​ 　　其中，在每一代的Discriminator和Generator的对抗过程中，我们可以形象的用下图Discriminator和Generator的对话来描述

而我们在训练过程中，算法要分为两个步骤：

• 1. 固定Generator，训练Discriminator　

  ​ 　　而当我们在训练Discriminator的时候，不能一味的投入好的数据给我们的Discriminator, 这样会使得我们的Discriminator认为所有的图片都是好的

  

  ​ 　　所以，我们常常需要添加一些负样本来使我们Discriminator知道，哪一些是好的数据，我们应该给他高分，哪一些是不好的数据，我们应该给它低分．

  

  

• 2. 固定Discriminator，训练Generator

  

• 算法总流程

  

为什么GAN可以？

​ 　　在GAN生成动漫头像的过程中，我们其实使用我们自己制造的数据分布来拟合真实的数据分布，我们希望我们自己制造的数据分布能越来越像真实的数据分布．

​ 　　在下图中，我们可以很直观的看到，在初始状态时，我们的Discriminator给了真实的数据很高的分数，而由Generator生成的的数据我们给了低分．接着，Generator开始学习这种这种真实的数据分布，经过一代的调整，Generator的数据分布移向了真实的数据分布的附近，此时，Discriminator相应的会提高由Generator所产生的数据分布的分数．如此往复，最终，我们正式的数据分布和Generator产生的数据分布近似重叠在一起，这时Discriminator不能进行有效的判断．

​ 　　而在真实训练的过程中，我们也是在寻找这种拟合真实数据的分布，所以，假设我们现在的Generator的数据分布为高斯分布：$P_G(x:\theta )$，$\theta$为高斯函数的的均值和方差，也是我们待估计的参数，我们可以通过使用极大似然估计在估计参数$\theta$．

​ 　　而最后极大似然估计会转为求解KL Divergence（理解：KL散度的理解），然后，我们通过极小化KL Divergence来使得两个数据分布更加的接近．

我们在训练过程中Generator和Discriminator各自的目的也不同，如下：

• Generator的目的

• Discriminator的目的

​ 　　我们在训练Discriminator时，需要固定值Generator的参数，来训练Discriminator．在下面的$V(G,D)$的式子中，我们希望我们的Discriminator能够对来自样本的数据打高分，对Generator生成的数据给低分，这样使得我们最后在极大化$V$函数下求的最优的Discriminator．

​ 　　训练得到最佳的Discriminator带入原函数，得到最大化后的$V(G,D^{\ast })$，进过化简之后我们得到真实数据分布和Generator生成数据的Jensen-Shannon divergence（理解：KL散度、JS散度、Wasserstein距离）

​ 　　所以，我们最后的训练变成一个极小极大问题，在下图中绿色的虚线描述了JSD，我们可以观察得到G3的JSD最小，及此时能够描述两个数据分布越接近．

​ 　　我们为了寻找最好的Generator，使用了梯度下降法来更新参数（实验中使用Adam算法），而此时我们在对函数求导时存在多个不同的函数，所以，在每一次参数更新之后，我们都要重新选择一个最大函数来作为下一次梯度更新函数．

​ 　　所以，最后算法的整体流程如下，我们首先固定初代的$G_0$,训练我们的Discriminator，找到$D_0^{\ast }$使得我们得到最大的$V(G_0,D$)

．　接下来，使用梯度下降法来最小化我们的$V(G_0,D)$(等价于JS divergence)得到$G_1$，然后，固定$G_1$，如此往复．．．．．

注意:实际上，我们在训练的时候，要掌握Generator和Discriminator的训练次数，我们希望我们的Discriminator能够尽可能的得到我们的最大值，而对于我们的Generator，我们希望它每次只更新一点点，因为如果我们的Generator每一次的更新浮动过大，可能会造成我们在下一次的$V(D^{\ast },G)$变大，这使得我们原本通过不断减少JSD来拟合真实的数据分布变得更加困难．所以，我们希望在训练Generator时，不要更新的过多（在后面的实验中也会讨论这一部分的问题）

Pytorch实现

1.模型搭建

Generator

• Pytorch实现

  class NetG(nn.Module):
      """
      定义一个生成模型，通过输入噪声来产生一张图片
      """
  
      def __init__(self, opt):
          super(NetG, self).__init__()
          # ngf = self.ngf  # 生成器的特征图数目
          ngf = opt.ngf
          self.main = nn.Sequential(
              # 假定输入为一张1*1*opt.nz维的数据(opt.nz维的向量)
              nn.ConvTranspose2d(opt.nz , ngf * 8, 4, 1, 0, bias=False),
              nn.BatchNorm2d(ngf * 8),
              nn.ReLU(inplace=True),
  
              # 输入一个４*4*ngf*8
              nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
              nn.BatchNorm2d(ngf * 4),
              nn.ReLU(True),
  
              # 输入一个8*8*ngf*4
              nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=True),
              nn.BatchNorm2d(ngf * 2),
              nn.ReLU(True),
  
              # 输入一个16*16*ngf*2
              nn.ConvTranspose2d(ngf * 2, ngf, 4, 2, 1, bias=False),
              nn.BatchNorm2d(ngf),
              nn.ReLU(inplace=True),
  
              # 输入一个32*32*ngf
              nn.ConvTranspose2d(ngf, 3, 5, 3, 1, bias=False),
              nn.Tanh()
              # 输出一张96*96*3
          )
  
      def forward(self, x):
          return self.main(x)
  
  
  

• 可视化网络

  

Discriminator

• Pytorch实现

  class NetD(nn.Module):
      """
      构建一个判别器，相当与一个二分类问题, 生成一个值
      """
  
      def __init__(self, opt):
          super(NetD, self).__init__()
  
          ndf = opt.ndf
          self.main = nn.Sequential(
              # 输入96*96*3
              nn.Conv2d(3, ndf, 5, 3, 1, bias=False),
              nn.LeakyReLU(negative_slope=0.2, inplace=True),
  
              # 输入32*32*ndf
              nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
              nn.BatchNorm2d(ndf * 2),
              nn.LeakyReLU(0.2, True),
  
              # 输入16*16*ndf*2
              nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
              nn.BatchNorm2d(ndf * 4),
              nn.LeakyReLU(0.2, True),
  
              # 输入为8*8*ndf*4
              nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
              nn.BatchNorm2d(ndf * 8),
              nn.LeakyReLU(0.2, True),
  
              # 输入为4*4*ndf*8
              nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=True),
              nn.Sigmoid()  # 分类问题
          )
  
      def forward(self, x):
          return self.main(x).view(-1)
  
  

• 可视化网络

  

  2. 主文件

  import tqdm
  from models import NetD, NetG
  from tensorboardX import SummaryWriter
  import torch as t
  import torchvision as tv
  from torch.utils.data import DataLoader
  from config import opt
  import torch.nn as nn
  from torchnet.meter import AverageValueMeter
  
  
  def train(**kwargs):
      """training NetWork"""
  
      #  0.配置属性
      for k_, v_ in kwargs.items():
          setattr(opt, k_, v_)
  
      device = t.device("cuda") if opt.gpu else t.device("cpu")
  
      # 1.预处理数据
      transforms = tv.transforms.Compose([
          tv.transforms.Resize(opt.img_size),  # 3*96*96
          tv.transforms.CenterCrop(opt.img_size),
          tv.transforms.ToTensor(),
          tv.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
      ])
      #  1.1 加载数据
      dataset = tv.datasets.ImageFolder(opt.data_path, transform=transforms)  # TODO 复习这个封装方法
      dataloader = DataLoader(dataset,
                              batch_size=opt.batch_size,
                              shuffle=True,
                              num_workers=opt.num_workers,
                              drop_last=True)  # TODO 查看drop_last操作
  
      # 2．初始化网络
      netg, netd = NetG(opt), NetD(opt)
      # 2.1判断网络是否已有权重数值
      map_location = lambda storage, loc: storage  # TODO 复习map_location操作
  
      if opt.netg_path:
          netg.load_state_dict(t.load(opt.netg_path, map_location=map_location))
      if opt.netd_path:
          netd.load_state_dict(t.load(opt.netd_path, map_location=map_location))
      # 2.2 搬移模型到指定设备
      netd.to(device)
      netg.to(device)
  
      # 3. 定义优化策略
      #  TODO 复习Adam算法
      optimize_g = t.optim.Adam(netg.parameters(), lr=opt.lr1, betas=(opt.beta1,
                                                                      0.999))
      optimize_d = t.optim.Adam(netd.parameters(), lr=opt.lr2, betas=(opt.beta1,
                                                                      0.999))
      criterions = nn.BCELoss().to(device)  # TODO 重新复习BCELoss方法
  
      # 4. 定义标签, 并且开始注入生成器的输入noise
      true_labels = t.ones(opt.batch_size).to(device)
      fake_labels = t.ones(opt.batch_size).to(device)
      noises = t.randn(opt.batch_size, opt.nz, 1, 1).to(device)
      fix_noises = t.randn(opt.batch_size, opt.nz, 1, 1).to(device)
  
      errord_meter = AverageValueMeter()  # TODO 重新阅读torchnet
      errorg_meter = AverageValueMeter()
  
      #  6.训练网络
      epochs = range(opt.max_epoch)
      write = SummaryWriter(log_dir=opt.virs, comment='loss')
  
      # 6.1 设置迭代
      for epoch in iter(epochs):
          #  6.2 读取每一个batch 数据
          for ii_, (img, _) in tqdm.tqdm(enumerate(dataloader)):
              real_img = img.to(device)
  
              #  6.3开始训练生成器和判别器
              #  注意要使得生成的训练次数小于一些
              if ii_ % opt.d_every == 0:
                  optimize_d.zero_grad()
                  # 训练判别器
                  # 真图
                  output = netd(real_img)
                  error_d_real = criterions(output, true_labels)
                  error_d_real.backward()
  
                  # 随机生成的假图
                  noises = noises.detach()
                  fake_image = netg(noises).detach()
                  output = netd(fake_image)
                  error_d_fake = criterions(output, fake_labels)
                  error_d_fake.backward()
                  optimize_d.step()
  
                  # 计算loss
                  error_d = error_d_fake + error_d_real
                  errord_meter.add(error_d.item())
  
              # 训练判别器
              if ii_ % opt.g_every == 0:
                  optimize_g.zero_grad()
                  noises.data.copy_(t.randn(opt.batch_size, opt.nz, 1, 1))
                  fake_img = netg(noises)
                  output = netd(fake_img)
                  error_g = criterions(output, true_labels)
                  error_g.backward()
                  optimize_g.step()
  
                  errorg_meter.add(error_g.item())
              # 绘制数据
              if ii_ % 5 == 0:
                  write.add_scalar("Discriminator_loss", errord_meter.value()[0])
                  write.add_scalar("Generator_loss", errorg_meter.value()[0])
  
          #  7.保存模型
          if (epoch + 1) % opt.save_every == 0:
              fix_fake_image = netg(fix_noises)
              tv.utils.save_image(fix_fake_image.data[:64], "%s/%s.png" % (
                  opt.save_path, epoch), normalize=True)
  
              t.save(netd.state_dict(), 'checkpoints/netd_%s.pth' % epoch)
              t.save(netg.state_dict(), 'checkpoints/netg_%s.pth' % epoch)
              errord_meter.reset()
              errorg_meter.reset()
  
      write.close()
  
  
  @t.no_grad()
  def generate(**kwargs):
      """用训练好的数据进行生成图片"""
  
      for k_, v_ in kwargs.items():
          setattr(opt, k_, v_)
  
      device = t.device("cuda" if opt.gpu else "cpu")
  
      #  1.加载训练好权重数据
      netg, netd = NetG(opt).eval(), NetD(opt).eval()
      map_location = lambda storage, loc: storage
  
      netd.load_state_dict(t.load(opt.netd_path, map_location=map_location), False)
      netg.load_state_dict(t.load(opt.netg_path, map_location=map_location), False)
      netd.to(device)
      netg.to(device)
  
      #  2.生成训练好的图片
      noise = t.randn(opt.gen_search_num, opt.nz, 1, 1).normal_(opt.gen_mean,
                                                                opt.gen_std)
      noise.to(device)
  
      fake_image = netg(noise)
      score = netd(fake_image).detach()  # TODO 查阅topk()函数
  
      # 挑选出合适的图片
      indexs = score.topk(opt.gen_num)[1]
  
      result = []
  
      for ii in indexs:
          result.append(fake_image.data[ii])
  
      tv.utils.save_image(t.stack(result), opt.gen_img, normalize=True, range=(-1, 1))
  
  
  if __name__ == "__main__":
      import fire
      fire.Fire()
  

3.实验分析

实验数据 1: Generator 训练1次，Discriminator 训练5次　总迭代200次（推荐）

实验效果:

迭代次数:1	迭代次数:50
迭代次数:100	迭代次数:200

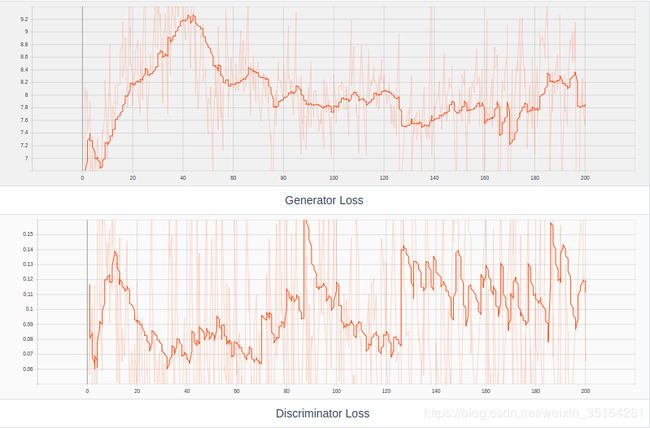
Loss:

实验结论：

​ 　　从实验本身的效果可以观察到，Generator在初期生成一张随机的图片，迭代50次之后，Generator生成的图片已经逐渐有了一定的形状，随着不断增加增加迭代次数，Generator生成的图片也越来越清晰，次数只是迭代2000次后的结构，后期增加了迭代次数到1400次，具体看实验数据2.我们观察生成的Loss图像可以看出Generator和Discriminator的对抗过程，两者你强我弱，此消彼长．

实验数据 2: Generator 训练5次，Discriminator 训练1次　总迭代1400次

实验效果：（B站视频链接）

Loss:

实验结论:

​ 　　本次实验只是增加了迭代次数，希望能够高Generator生成图片的质量，但是在迭代到750次之后，Generator生成的图片变成了和迭代一次之后的效果，并且之后Generator不在生成好的图片，由Generator的Loss损失函数也是在750次之后突然骤升，暂时还未知道具体细节．（推荐看：GAN的Loss为什么降不下去）

实验数据 3: Generator 训练1次，Discriminator 训练1次　迭代200次

实验效果：

迭代次数:1	迭代次数:50
迭代次数:100	迭代次数:200

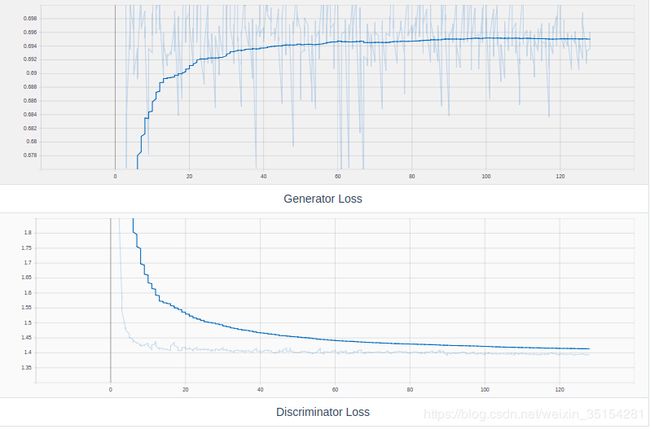
Loss

​ 　　本次实验旨在验证，如果Discriminator和Generator的训练次数相等，会出现什么结果？从实验效果直观的可以观察到，在初代的Generator生成的图片中，我们就已经得到了动漫头像的雏形，迭代到了200次已经有较好的动漫头像，相比与Discriminator和Generator的训练次数5:1的结果，整体效果会稍微好一点．这和理论有一点出入，后续会补充．

实验数据４: Generator 训练5次，Discriminator 训练1次　迭代200次

实验效果：

迭代次数:1	迭代次数:50
迭代次数:100	迭代次数:190

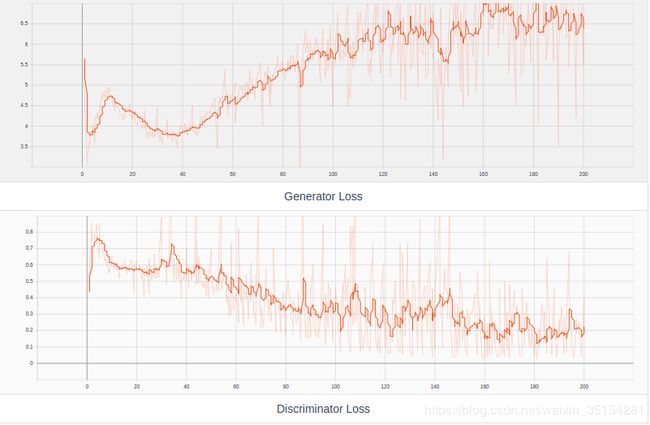
Loss:

实验结论：

​ 　　从实验效果可以直观的看出,如果Discriminator和Generator的训练次数比为5:1，Generator生成的头像非常的差，此时的Discriminator Loss也呈现不断下降的趋势，说明我们通过Generator生成的图片很容易就被我们的Discriminator辨别为假．这是我们不希望看到的．

总结

​ 　　本文从ＧＡＮ的理解到原理，并且围绕GAN生成动漫头像，系统的梳理了自己第一次学习GAN的知识，旨在是自己能够对GAN有一个清晰认识，在实践过程中也是对一些知识点进行了探索，如实验数据3和4中，对于Discriminator和Generator进行了调整，解决了自己的一些疑问，也验证了＂Discriminator的训练次数大于Generator是好的＂，并且这样的训比重使得训练时间缩短了不少．除此之外，此次生成的动漫头像无论是清晰度还是真实性上都有所不足，后期继续学习会进行更改．数据已上传百度网盘可直接下载，代码已上传GitHub．如果在阅读过程中发现什么错误，务必请您及时指出，共同学习，谢谢． 最近发现一个好东西放出来和大家一起享用GanLab

参考链接

GAN paper

李宏毅GAN视频

GAN的Loss为什么降不下去

pytorch-book

百度网盘数据集

提取码：sedf

KL散度的理解

KL散度、JS散度、Wasserstein距离