安替-AnTi

TensorFlow 2.0深度学习算法实战(一)

第一章人工智能绪论

1.1 人工智能

信息技术是人类历史上的第三次工业革命，计算机、互联网、智能家居等技术的普及
极大地方便了人们的日常生活。通过编程的方式，人类可以将提前设计好的交互逻辑重复
且快速地执行，从而将人类从简单枯燥的重复劳动任务中解脱出来。但是对于需要较高智
能的任务，如人脸识别，聊天机器人，自动驾驶等任务，很难设计明确的逻辑规则，传统
的编程方式显得力不从心，而人工智能技术是有望解决此问题的关键技术。

随着深度学习算法的崛起，人工智能在部分任务上取得了类人甚至超人的水平，如围
棋上 AlphaGo 智能程序已经击败人类最强围棋专家柯洁，在 Dota2 游戏上 OpenAI Five 智
能程序击败冠军队伍 OG，同时人脸识别，智能语音，机器翻译等一项项实用的技术已经
进入到人们的日常生活中。现在我们的生活处处被人工智能环绕，尽管目前达到的智能水
平离通用人工智能(Artificial General Intelligence，简称 AGI)还有一段距离，我们仍坚定相
信人工智能时代即将来临。
接下来我们将介绍人工智能，机器学习，深度学习的概念以及它们之间的联系与区
别。

1.1.1 人工智能

人工智能是指让机器获得像人类一样的智能机制的技术，这一概念最早出现在 1956 年
召开的达特茅斯会议上。这是一项极具挑战性的任务，人类目前尚无法对人脑的工作机制
有全面科学的认知，希望能制造达到人脑水平的智能机器无疑是难于上青天。即使如此，
在某个方面呈现出类似、接近甚至超越人类智能水平的机器被证明是可行的。

怎么实现人工智能是一个非常广袤的问题。人工智能的发展主要经历过 3 种阶段，每
个阶段都代表了人类从不同的角度尝试实现人工智能的探索足迹。最早期人类试图通过总
结、归纳出一些逻辑规则，并将逻辑规则以计算机程序的方式来开发智能系统。但是这种
显式的规则往往过于简单，很难表达复杂、抽象的规则。这一阶段被称为推理期。

1970 年代，科学家们尝试通过知识库+推理的方式解决人工智能，通过构建庞大复杂
的专家系统来模拟人类专家的智能水平。这些明确指定规则的方式存在一个最大的难题，
就是很多复杂，抽象的概念无法用具体的代码实现。比如人类对图片的识别，对语言的理
解过程，根本无法通过既定规则模拟。为了解决这类问题，一门通过让机器自动从数据中
学习规则的研究学科诞生了，称为机器学习，并在 1980 年代成为人工智能中的热门学科。

在机器学习中，有一门通过神经网络来学习复杂、抽象逻辑的方向，称为神经网络。
神经网络方向的研究经历了 2 起 2 落，并从 2012 年开始，由于效果极为显著，应用深层神
经网络技术在计算机视觉、自然语言处理、机器人等领域取得了重大突破，部分任务上甚
至超越了人类智能水平，开启了以深层神经网络为代表的人工智能的第 3 次复兴。深层神
经网络有了一个新名字，叫做深度学习，一般来讲，神经网络和深度学习的本质区别并不
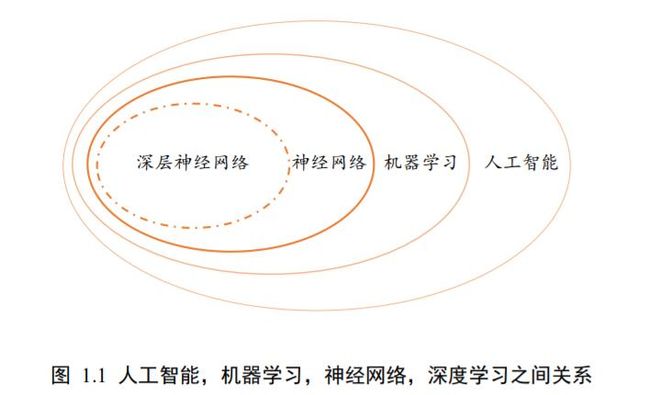
大，深度学习特指基于深层神经网络实现的模型或算法。人工智能，机器学习，神经网
络，深度学习的相互之间的关系如图所示。

1.1.2 机器学习

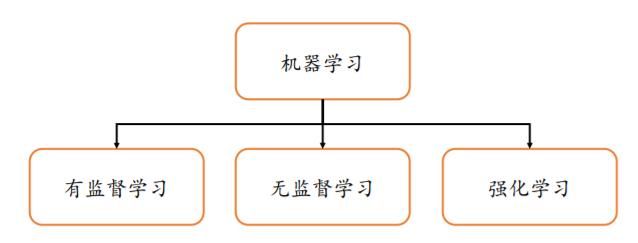
机器学习可以分为有监督学习(Supervised Learning)、无监督学习(Unsupervised
Learning)和强化学习(Reinforcement Learning)，如图所示：

有监督学习 有监督学习的数据集包含了样本与样本的标签，算法模型需要学习到映射
: → ，其中代表模型函数，为模型的参数。在训练时，通过计算模型的预测值
()与真实标签之间的误差来优化网络参数，使得网络下一次能够预测更精准。常见的
有监督学习有线性回归，逻辑回归，支持向量机，随机森林等。

无监督学习 收集带标签的数据往往代价较为昂贵，对于只有样本的数据集，算法需要自
行发现数据的模态，这种方式叫做无监督学习。无监督学习中有一类算法将自身作为监督
信号，即模型需要学习的映射为: → ，称为自监督学习(Self-supervised Learning)。在
训练时，通过计算模型的预测值()与自身之间的误差来优化网络参数。常见的无监督
学习算法有自编码器，生成对抗网络等。

强化学习也称为增强学习，通过与环境进行交互来学习解决问题的策略的一类算法。与有监督、无监督学习不同，强化学习问题并没有明确的“正确的”动作监督信号，算法需要与环境进行交互，获取环境反馈的滞后的奖励信号，因此并不能通过计算动作与“正确动作”之间的误差来优化网络。常见的强化学习算法有 DQN，PPO 等。

1.1.3 神经网络与深度学习

神经网络算法是一类通过神经网络从数据中学习的算法，它仍然属于机器学习的范畴。受限于计算能力和数据量，早期的神经网络层数较浅，一般在 1~4 层左右，网络表达能力有限。随着计算能力的提升和大数据时代的到来，高度并行化的 GPU 和海量数据让大规模神经网络的训练成为可能。

2006 年，Geoffrey Hinton(杰弗里希尔顿) 首次提出深度学习的概念，2012 年，8 层的深层神经网络 AlexNet 发布，并在图片识别竞赛中取得了巨大的性能提升，此后数十层，数百层，甚至上千层的神经网络模型相继提出，展现出深层神经网络强大的学习能力。我们一般将利用深层神经网络实现的算法或模型称作深度学习，本质上神经网络和深度学习是相同的。

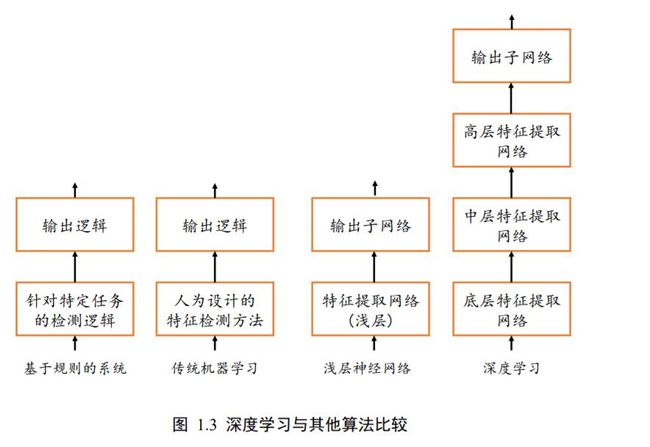
我们来比较一下深度学习算法与其他算法，如图 1.3 所示。基于规则的系统一般会编写显示的规则逻辑，这些逻辑一般是针对特定的任务设计的，并不适合其他任务。传统的机器学习算法一般会人为设计具有一定通用性的特征检测方法，如 SIFT，HOG 特征，这些特征能够适合某一类的任务，具有一定的通用性，但是如何设计特征方法，特征方法的好坏是问题的关键。神经网络的出现，使得人为设计特征这一部分工作可以通过神经网络让机器自动学习，不需要人类干预。但是浅层的神经网络的特征提取能力较为有限，而深层的神经网络擅长提取深层，抽象的高层特征，因此具有更好的性能表现。

1.2 神经网络发展简史

我们将神经网络的发展历程大致分为浅层神经网络阶段和深度学习阶段，以 2006 年为分割点。2006 年以前，深度学习以神经网络和连接主义名义发展，历经了 2 次兴盛和 2 次寒冬；在 2006 年，Geoffrey Hinton 首次将深层神经网络命名为深度学习，开启了深度学习
的第 3 次复兴之路。

1.2.1 浅层神经网络

1943 年，心理学家 Warren McCulloch 和逻辑学家 Walter Pitts 根据生物神经元(Neuron)结构，提出了最早的神经元数学模型，称为 MP 神经元模型。该模型的输出() =ℎ(())，其中() = ∑ , ∈ {0,1}，模型通过()的值来完成输出值的预测，如果() ≥ ，输出为 1；如果() < ，输出为 0。可以看到，MP 神经元模型并没有学习能力，只能完成固定逻辑的判定。

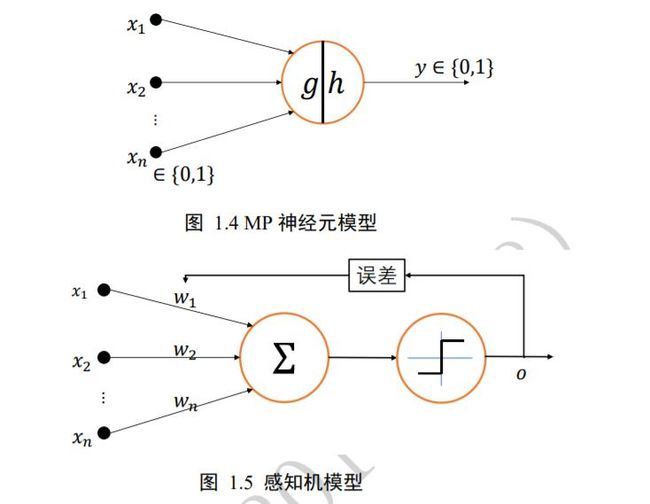
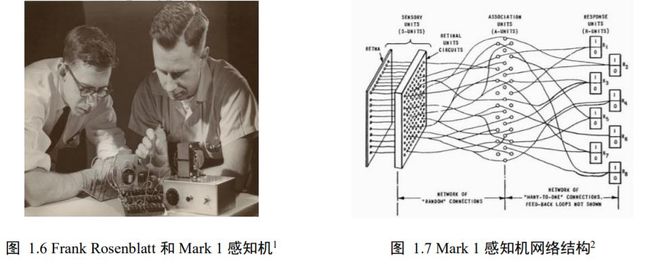
1958 年，美国心理学家 Frank Rosenblatt 提出了第一个可以自动学习权重的神经元模型，称为感知机(Perceptron)，如图 1.5 所示，输出值与真实值之间的误差用于调整神经元的权重参数{ $w_{1},w_{2},...,w_{n}$ )。感知机随后基于“Mark 1 感知机”硬件实现，如图 1.6 、1.7 所示，输入为 400 个单元的图像传感器，输出为 8 个节点端子，可以成功识别一些英文字母。我们一般认为 1943 年~1969 年为人工智能发展的第一次兴盛期。

1969 年，美国科学家 Marvin Minsky 等人在出版的《Perceptrons》一书中指出了感知机等线性模型的主要缺陷，即无法处理简单的异或 XOR 等线性不可分问题。这直接导致了以感知机为代表的神经网络相关研究进入了低谷期，一般认为 1969 年~1982 年为人工智能发展的第一次寒冬。

尽管处于 AI 发展的低谷期，仍然有很多意义重大的研究相继发表，这其中最重要的成果就是反向传播算法(Backpropagation，简称 BP 算法)的提出，它依旧是现代深度学习的核心理论基础。实际上，反向传播的数学思想早在 1960 年代就已经被推导出了，但是并没有应用在神经网络上。直到 1974 年，美国科学家 Paul Werbos 在他的博士论文中第一次提出可以将 BP 算法应用到神经网络上，遗憾的是，这一成果并没有获得足够重视。直至1986 年，David Rumelhart 等人在 Nature 上发表了通过 BP 算法来表征学习的论文，BP 算法才获得了广泛的关注。

1982 年 John Hopfild 的循环连接的 Hopfield 网络的提出，开启了 1982 年~1995 年的第二次人工智能复兴的大潮，这段期间相继提出了卷积神经网络，循环神经网络，反向传播算法等算法模型。1986 年，David Rumelhart 和 Geoffrey Hinton 等人将 BP 算法应用在多层感知机上；1989 年Yann LeCun 等人将 BP 算法应用在手写数字图片识别上，取得了巨大成功，这套系统成功商用在邮政编码识别、银行支票识别等系统上；1997 年，应用最为广泛的循环神经网络变种之一 LSTM 被 Jürgen Schmidhuber 提出；同年双向循环神经网络也被提出。

遗憾的是，神经网络的研究随着以支持向量机(Support Vector Machine，简称 SVM)为
代表的传统机器学习算法兴起而逐渐进入低谷，称为人工智能的第二次寒冬。支持向量机
拥有严格的理论基础，需要的样本数量较少，同时也具有良好的泛化能力，相比之下，神
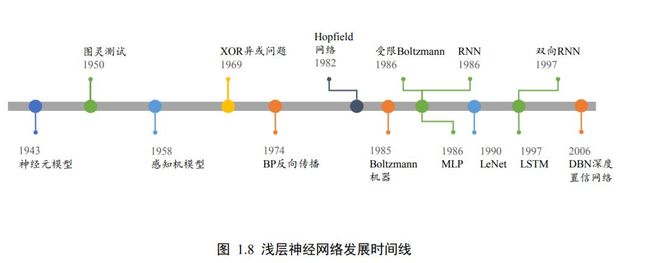
经网络理论基础欠缺，可解释性差，很难训练深层网络，性能也一般。图 1.8 画出了 1943
年~2006 年之间的重大时间节点。

1.2.2 深度学习

2006 年，Geoffrey Hinton 等人发现通过逐层预训练的方式可以较好地训练多层神经网络，并在 MNIST 手写数字图片数据集上取得了优于 SVM 的错误率，开启了第 3 次人工智能的复兴。在论文中，Geoffrey Hinton 首次提出了 Deep Learning 的概念，这也是(深层)神经网络被叫做深度学习的由来。2011 年，Xavier Glorot 提出了线性整流单元(Rectified Linear Unit, ReLU)激活函数，这是现在使用最为广泛的激活函数之一。2012 年，Alex Krizhevsky 提出了 8 层的深层神经网络 AlexNet，它采用了 ReLU 激活函数，并使用 Dropout 技术防止过拟合，同时抛弃了逐层预训练的方式，直接在 2 块 GTX580 GPU 上训练网络。AlexNet 在 ILSVRC-2012 图片识别比赛中获得了第一名，比第二名在 Top-5 错误率上降低了惊人的 10.9%。

自 AlexNet 模型提出后，各种各样的算法模型相继被发表，其中有 VGG 系列，GoogleNet，ResNet 系列，DenseNet 系列等等，其中 ResNet 系列网络实现简单，效果显著，很快将网络的层数提升至数百层，甚至上千层，同时保持性能不变甚至更好。

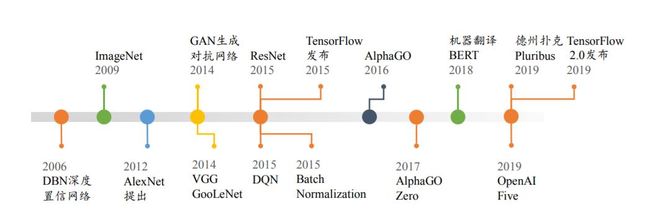
除了有监督学习领域取得了惊人的成果，在无监督学习和强化学习领域也取得了巨大的成绩。2014 年，Ian Goodfellow 提出了生成对抗网络，通过对抗训练的方式学习样本的真实分布，从而生成逼近度较高的图片。此后，大量的生成对抗网络模型被提出，最新的图片生成效果已经达到了肉眼难辨真伪的逼真度。2016 年，DeepMind 公司应用深度神经网络到强化学习领域，提出了 DQN 算法，在 Atari 游戏平台中的 49 个游戏取得了人类相当甚至超越人类的水平；在围棋领域，DeepMind 提出的 AlphaGo 和 AlphaGo Zero 智能程序相继打败人类顶级围棋专家李世石、柯洁等；在多智能体协作的 Dota2 游戏平台，OpenAI 开发的 OpenAI Five 智能程序在受限游戏环境中打败了 TI8 冠军 OG 队，展现出了大量专业级的高层智能的操作。图 1.9 列出了 2006 年~2019 年之间重大的时间节点。

1.3 深度学习特点

与传统的机器学习算法、浅层神经网络相比，现代的深度学习算法通常具有如下特点。

1.3.1 数据量

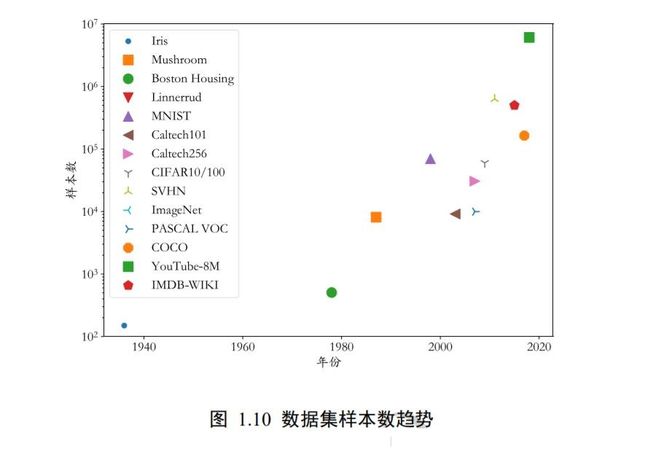
早期的机器学习算法比较简单，容易快速训练，需要的数据集规模也比较小，如 1936年由英国统计学家 Ronald Fisher 收集整理的鸢尾花卉数据集 Iris 共包含 3 个类别花卉，每个类别 50 个样本。随着计算机技术的发展，设计的算法越来越复杂，对数据量的需求也随之增大。1998 年由 Yann LeCun 收集整理的 MNIST 手写数字图片数据集共包含 0~9 共 10类数字，每个类别多达 7000 张图片。随着神经网络的兴起，尤其是深度学习，网络层数较深，模型的参数量成百上千万个，为了防止过拟合，需要的数据集的规模通常也是巨大的。现代社交媒体的流行也让收集海量数据成为可能，如 2010 年的ImageNet 数据集收录了 14,197,122 张图片，整个数据集的压缩文件大小就有 154GB。

尽管深度学习对数据集需求较高，收集数据，尤其是收集带标签的数据，往往是代价昂贵的。数据集的形成通常需要手动采集、爬取原始数据，并清洗掉无效样本，再通过人类智能去标注数据样本，因此不可避免地引入主观偏差和随机误差。因此研究数据量需求较少的算法模型是非常有用的一个方向。

1.3.2 计算力

计算能力的提升是第三次人工智能复兴的一个重要因素。实际上，目前深度学习的基础理论在 1980 年代就已经被提出，但直到 2012 年基于 2 块 GTX580 GPU 训练的 AlexNet发布后，深度学习的真正潜力才得以发挥。传统的机器学习算法并不像神经网络这样对数据量和计算能力有严苛的要求，通常在 CPU 上串行训练即可得到满意结果。但是深度学习非常依赖并行加速计算设备，目前的大部分神经网络均使用 NVIDIA GPU 和 Google TPU或其他神经网络并行加速芯片训练模型参数。如围棋程序 AlphaGo Zero 在 64 块 GPU 上从零开始训练了 40 天才得以超越所有的 AlphaGo 历史版本；自动网络结构搜索算法使用了800 块 GPU 同时训练才能优化出较好的网络结构。

目前普通消费者能够使用的深度学习加速硬件设备主要来自 NVIDIA 的 GPU 显卡，图 1.12 例举了从 2008 年到 2017 年 NVIDIA GPU 和 x86 CPU 的每秒 10 亿次的浮点运算数(GFLOPS)的指标变换曲线。可以看到，x86 CPU 的曲线变化相对缓慢，而 NVIDIA GPU的浮点计算能力指数式增长，这主要是由日益增长的游戏计算量和深度学习计算量等驱动的。

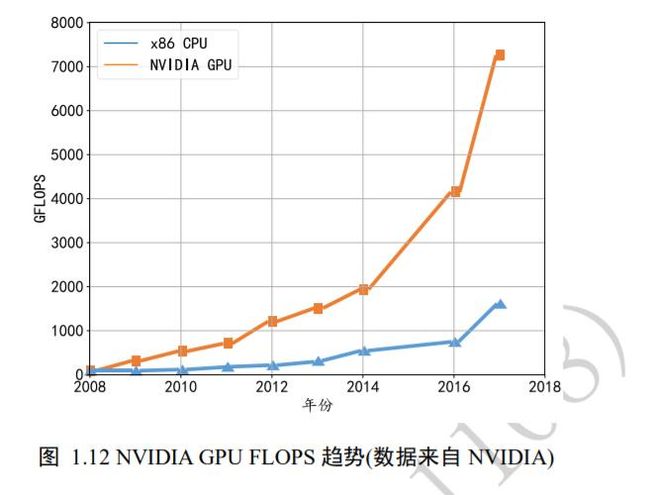
1.3.3 网络规模

早期的感知机模型和多层神经网络层数只有 1 层或者 2~4 层，网络参数量也在数万左右。随着深度学习的兴起和计算能力的提升，AlexNet(8 层)，VGG16(16 层)，GoogLeNet(22 层)，ResNet50(50 层)，DenseNet121(121 层)等模型相继被提出，同时输入图片的大小也从 28x28 逐渐增大，变成 224x224，299x299 等，这些使得网络的总参数量可达到千万级别，如图 1.13 所示。
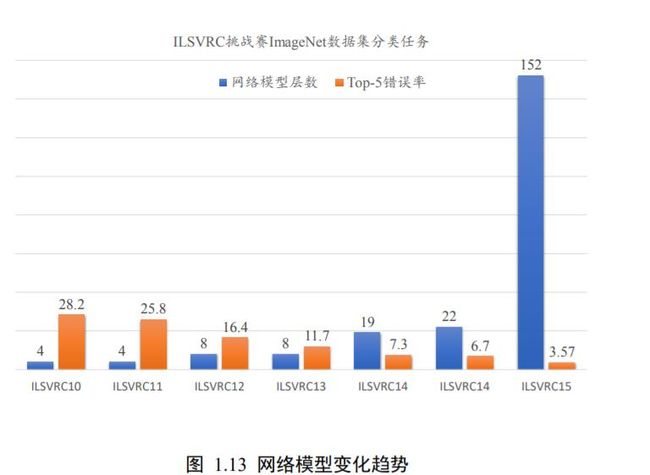网络规模的增大，使得神经网络的容量相应增大，从而能够学习到复杂的数据模态，模型的性能也会随之提升；另一方面，网络规模的增大，意味着更容易出现过拟合现象，训练需要的数据集和计算代价也会变大。

1.3.4 通用智能

在过去，为了提升某项任务上的算法性能，往往需要手动设计相应的特征和先验设定，以帮助算法更好地收敛到最优解。这类特征或者先验往往是与具体任务场景强相关的，一旦场景发生了变动，这些依靠人工设计的特征或先验无法自适应新场景，往往需要重新设计算法模型，模型的通用性不强。

设计一种像人脑一样可以自动学习、自我调整的通用智能机制一直是人类的共同愿景。深度学习从目前来看，是最接近通用智能的算法之一。在计算机视觉领域，过去需要针对具体的任务设计征、添加先验的做法，已经被深度学习完全抛弃了，目前在图片识别、目标检测、语义分割等方向，几乎全是基于深度学习端到端地训练，获得的模型性能好，适应性强；在 Atria 游戏平台上，DeepMind 设计的 DQN 算法模型可以在相同的算法、模型结构和超参数的设定下，在 49 个游戏上获得人类相当的游戏水平，呈现出一定程度的通用智能。图 1.14 是 DQN 算法的网络结构，它并不是针对于某个游戏而设计的，而是可以运行在所有的 Atria 游戏平台上的 49 个游戏。

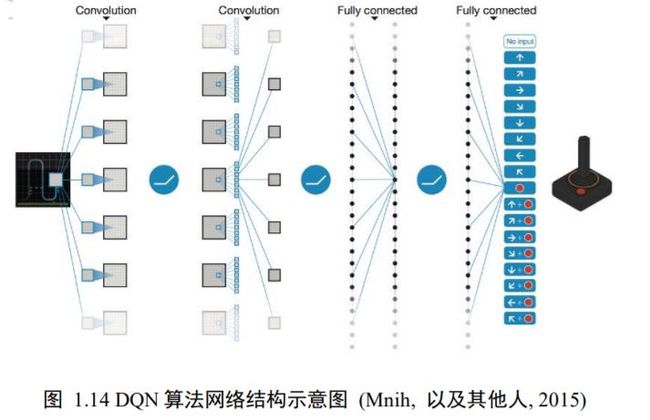
1.4 深度学习应用

深度学习算法已经广泛应用到人们生活的角角落落，例如手机中的语音助手，汽车上的智能辅助驾驶，人脸支付等等。我们将从计算机视觉、自然语言处理和强化学习 3 个领域入手，为大家介绍深度学习的一些主流应用。

1.4.1 计算机视觉

图片识别(Image Classification) 是常见的分类问题。神经网络的输入为图片数据，输出值为当前样本属于每个类别的概率，通常选取概率值最大的类别作为样本的预测类别。图片识别是最早成功应用深度学习的任务之一，经典的网络模型有 VGG 系列、Inception 系列、ResNet 系列等。

目标检测(Object Detection) 是指通过算法自动检测出图片中常见物体的大致位置，通常用边界框(Bounding box)表示，并分类出边界框中物体的类别信息，如图 1.15 所示。常见的目标检测算法有 RCNN，Fast RCNN，Faster RCNN，Mask RCNN，SSD,YOLO 系列等。

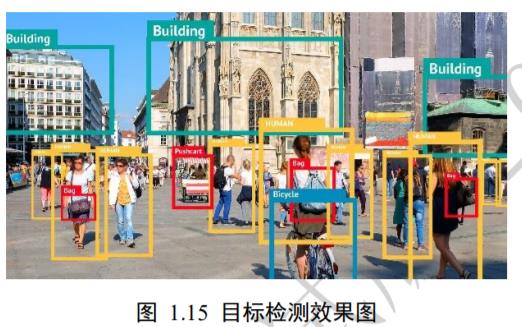
语义分割(Semantic Segmentation) 是通过算法自动分割并识别出图片中的内容，可以将语义分割理解为每个像素点的分类问题，分析每个像素点属于物体的类别，如图 1.16 所示。常见的语义分割模型有 FCN，U-net，SegNet，DeepLab 系列等。

视频理解(Video Understanding) 随着深度学习在 2D 图片的相关任务上取得较好的效果，具有时间维度信息的 3D 视频理解任务受到越来越多的关注。常见的视频理解任务有视频分类，行为检测，视频主体抽取等。常用的模型有 C3D，TSN，DOVF，TS_LSTM等。

图片生成(Image Generation) 通过学习真实图片的分布，并从学习到的分布中采样而获得逼真度较高的生成图片。目前主要的生成模型有 VAE 系列，GAN 系列等。其中 GAN 系列算法近年来取得了巨大的进展，最新 GAN 模型产生的图片样本达到了肉眼难辨真伪的效果，如图 1.17 为 GAN 模型的生成图片。

除了上述应用，深度学习还在其他方向上取得了不俗的效果，比如艺术风格迁移(图1.18)，超分辨率，图片去燥/去雾，灰度图片着色等等一系列非常实用酷炫的任务，限于篇幅，不再敖述。

1.4.2 自然语言处理

机器翻译(Machine Translation) 过去的机器翻译算法通常是基于统计机器翻译模型，这也是 2016 年前 Google 翻译系统采用的技术。2016 年 11 月，Google 基于 Seq2Seq 模型上线了 Google 神经机器翻译系统(GNMT)，首次实现了源语言到目标语言的直译技术，在多项任务上实现了 50~90%的效果提升。常用的机器翻译模型有 Seq2Seq，BERT，GPT，GPT-2 等，其中 OpenAI 提出的 GPT-2 模型参数量高达 15 亿个，甚至发布之初以技术安全考虑为由拒绝开源 GPT-2 模型。

聊天机器人(Chatbot) 聊天机器人也是自然语言处理的一项主流任务，通过机器自动与人类对话，对于人类的简单诉求提供满意的自动回复，提高客户的服务效率和服务质量。常应用在咨询系统、娱乐系统，智能家居等中。

1.4.3 强化学习

虚拟游戏 相对于真实环境，虚拟游戏平台既可以训练、测试强化学习算法，有可以避免无关干扰，同时也能将实验代价降到最低。目前常用的虚拟游戏平台有 OpenAI Gym，OpenAI Universe，OpenAI Roboschool，DeepMind OpenSpiel，MuJoCo 等，常用的强化学习算法有 DQN，A3C，A2C，PPO 等。在围棋领域，DeepMind AlaphGo 程序已经超越人类围棋专家；在 Dota2 和星际争霸游戏上，OpenAI 和 DeepMind 开发的智能程序也在限制规则下战胜了职业队伍。

机器人(Robotics) 在真实环境中，机器人的控制也取得了一定的进展。如 UC Berkeley在机器人的 Imitation Learning，Meta Learning，Few-shot Learning 等方向取得了不少进展。美国波士顿动力公司在人工智能应用中取得喜人的成就，其制造的机器人在复杂地形行走，多智能体协作等任务上表现良好(图 1.19)。

自动驾驶(Autonomous Driving) 被认为是强化学习短期内能技术落地的一个应用方向，很多公司投入大量资源在自动驾驶上，如百度、Uber，Google 无人车等，其中百度的无人巴士“阿波龙”已经在北京、雄安、武汉等地展开试运营，图 1.20 为百度的自动驾驶汽车。

1.5 深度学习框架

工欲善其事，必先利其器。在了解了深度学习及其发展简史后，我们来挑选一下深度学习要使用的工具吧。

1.5.1 主流框架

❑ Theano 是最早的深度学习框架之一，由 Yoshua Bengio 和 Ian Goodfellow 等人开发，是一个基于 Python 语言、定位底层运算的计算库，Theano 同时支持 GPU 和 CPU 运算。由于 Theano 开发效率较低，模型编译时间较长，同时开发人员转投 TensorFlow等原因，Theano 目前已经停止维护。

❑ Scikit-learn 是一个完整的面向机器学习算法的计算库，内建了常见的传统机器学习算法支持，文档和案例也较为丰富，但是 Scikit-learn 并不是专门面向神经网络而设计的，不支持 GPU 加速，对神经网络相关层实现也较欠缺。

❑ Caffe 由华人博士贾扬清在 2013 年开发，主要面向使用卷积神经网络的应用场合，并不适合其他类型的神经网络的应用。Caffe 的主要开发语言是 C++，也提供 Python 语言等接口，支持 GPU 和 CPU。由于开发时间较早，在业界的知名度较高，2017 年Facebook 推出了 Caffe 的升级版本 Cafffe2，Caffe2 目前已经融入到 PyTorch 库中。

❑ Torch 是一个非常优秀的科学计算库，基于较冷门的编程语言 Lua 开发。Torch 灵活性较高，容易实现自定义网络层，这也是 PyTorch 继承获得的优良基因。但是由于 Lua语言使用人群较小，Torch 一直未能获得主流应用。

❑ MXNET 由华人博士陈天奇和李沐等人开发，已经是亚马逊公司的官方深度学习框架。采用了命令式编程和符号式编程混合方式，灵活性高，运行速度快，文档和案例也较为丰富。

❑ PyTorch 是 Facebook 基于原有的 Torch 框架推出的采用 Python 作为主要开发语言的深度学习框架。PyTorch 借鉴了 Chainer 的设计风格，采用命令式编程，使得搭建网络和调试网络非常方便。尽管 PyTorch 在 2017 年才发布，但是由于精良紧凑的接口设计，PyTorch 在学术界获得了广泛好评。在 PyTorch 1.0 版本后，原来的 PyTorch 与 Caffe2进行了合并，弥补了 PyTorch 在工业部署方面的不足。总的来说，PyTorch 是一个非常优秀的深度学习框架。

❑ Keras 是一个基于 Theano 和 TensorFlow 等框架提供的底层运算而实现的高层框架，提供了大量方便快速训练，测试的高层接口，对于常见应用来说，使用 Keras 开发效率非常高。但是由于没有底层实现，需要对底层框架进行抽象，运行效率不高，灵活性一般。

❑ TensorFlow 是 Google 于 2015 年发布的深度学习框架，最初版本只支持符号式编程。得益于发布时间较早，以及 Google 在深度学习领域的影响力，TensorFlow 很快成为最流行的深度学习框架。但是由于 TensorFlow 接口设计频繁变动，功能设计重复冗余，符号式编程开发和调试非常困难等问题，TensorFlow 1.x 版本一度被业界诟病。2019年，Google 推出 TensorFlow 2 正式版本，将以动态图优先模式运行，从而能够避免TensorFlow 1.x 版本的诸多缺陷，已获得业界的广泛认可。

目前来看，TensorFlow 和 PyTorch 框架是业界使用最为广泛的两个深度学习框架，TensorFlow 在工业界拥有完备的解决方案和用户基础，PyTorch 得益于其精简灵活的接口设计，可以快速设计调试网络模型，在学术界获得好评如潮。TensorFlow 2 发布后，弥补了 TensorFlow 在上手难度方面的不足，使得用户可以既能轻松上手 TensorFlow 框架，又能无缝部署网络模型至工业系统。本书以 TensorFlow 2.0 版本作为主要框架，实战各种深度学习算法。

我们这里特别介绍 TensorFlow 与 Keras 之间的联系与区别。Keras 可以理解为一套高层 API 的设计规范，Keras 本身对这套规范有官方的实现，在 TensorFlow 中也实现了这套规范，称为 tf.keras 模块，并且 tf.keras 将作为 TensorFlow 2 版本的唯一高层接口，避免出现接口重复冗余的问题。如无特别说明，本书中 Keras 均指代 tf.keras。

1.5.2 TensorFlow 2 与 1.x

TensorFlow 2 是一个与 TensorFlow 1.x 使用体验完全不同的框架，TensorFlow 2 不兼容TensorFlow 1.x 的代码，同时在编程风格、函数接口设计等上也大相径庭，TensorFlow 1.x的代码需要依赖人工的方式迁移，自动化迁移方式并不靠谱。Google 即将停止支持TensorFlow 1.x，不建议学习 TensorFlow 1.x 版本。

TensorFlow 2 支持动态图优先模式，在计算时可以同时获得计算图与数值结果，可以代码中调试实时打印数据，搭建网络也像搭积木一样，层层堆叠，非常符合软件开发思维。

以简单的2.0 + 4.0的相加运算为例，在 TensorFlow 1.x 中，首先创建计算图：

import tensorflow as tf
# 1.创建计算图阶段
# 2.创建2个输入端子，指定类型和名字
a_ph=tf.placeholder(tf.float32,name='variable_a');
b_ph=tf.placeholder(tf.float32,name='variable_b');
# 创建输出端子的运算操作，并命名
c_op=tf.add(a_ph,b_ph,name='variable_a')

创建计算图的过程就类比通过符号建立公式 = + 的过程，仅仅是记录了公式的计算步骤，并没有实际计算公式的数值结果，需要通过运行公式的输出端子，并赋值 =2.0, = 4.0才能获得的数值结果：

#2. 运行计算图阶段
# 创建运行环境
sess=tf.InteractiveSession()
# 初始化步骤也需要为操作运行
init=tf.global_variables_initializer()
sess.run(init) #运行初始化操作，完成初始化
#运行端输出端子，需要给输入端子赋值
c_numpy=sess.run(c_op,feed_dict={a_ph:2.,b_ph:4.});
#运算完输出端子才能得到数值类型的c_numpy
print('a+b=',c_numpy)

可以看到，在 TensorFlow 中完成简单的2.0 + 4.0尚且如此繁琐，更别说创建复杂的神经网络算法有多艰难，这种先创建计算图后运行的编程方式叫做符号式编程。接下来我们使用 TensorFlow 2 来完成2.0 + 4.0运算：

# 1.创建输入张量
a=tf.constant(2.)
b=tf.constant(4.)
# 2.直接计算并打印
print('a+b=',a+b)

这种运算时同时创建计算图 + 和计算数值结果2.0 + 4.0的方式叫做命令式编程，也称为动态图优先模式。TensorFlow 2 和 PyTorch 都是采用动态图(优先)模式开发，调试方便，所见即所得。一般来说，动态图模型开发效率高，但是运行效率可能不如静态图模式，TensorFlow 2 也支持通过 tf.function 将动态图优先模式的代码转化为静态图模式，实现开发和运行效率的双赢。

1.5.3 功能演示

深度学习的核心是算法的设计思想，深度学习框架只是我们实现算法的工具。下面我们将演示 TensorFlow 深度学习框架的 3 大核心功能，从而帮助我们理解框架在算法设计中扮演的角色。

a) 加速计算
神经网络本质上由大量的矩阵相乘，矩阵相加等基本数学运算构成，TensorFlow 的重要功能就是利用 GPU 方便地实现并行计算加速功能。为了演示 GPU 的加速效果，我们通过完成多次矩阵 A 和矩阵 B 的矩阵相乘运算的平均运算时间来验证。其中矩阵 A 的 shape为[1,]，矩阵 B 的 shape 为[, 1]，通过调节 n 即可控制矩阵的大小。

首先我们分别创建使用 CPU 和 GPU 运算的 2 个矩阵：

# 创建在CPU上运行的2个矩阵
with tf.device('/cpu:0'):
  cpu_a=tf.random.random_normal([1,n])
  cpu_b=tf.random.random.normal([n,1])
  print(cpu_a.device,cpu_b.device)
# 创建使用GPU运算的2个矩阵
with tf.device('./gpu:0'):
  gpu_a=tf.random.normal([1,n])
  gpu_b=tf.random.normal([n,1])
  print(gpu_a.device,gpu_b.device)

并通过 timeit.timeit()函数来测量 2 个矩阵的运时间：

def cpu_run():
  with tf.device('./cpu:0'):
    c=tf.matmul(cpu_a,cpu_b)
  return c

def gpu_run():
  with tf.device('./gpu:0'):
    c=tf.matmul(gpu_a,gpu_b)
  return c

import timeit
# 第一次计算需要热身，避免将初始化阶段时间结算在内
cpu_time=timeit.timeit(cpu_run(),number=10)
gpu_time=timeit.timeit(gpu_run(),number=10)
print('Warmup:',cpu_time,gpu_time)
# 正式计算10次，取平均时间
cpu_time=timeit.timeit(cpu_run(),number=10)
gpu_time=timeit.timeit(gpu_run(),number=10)
print('rum time:',cpu_time,gpu_time)

我们将不同大小的 n 下的 CPU 和 GPU 的运算时间绘制为曲线，如图 1.21 所示。可以看到，在矩阵 A 和 B 较小时，CPU 和 GPU 时间几乎一致，并不能体现出 GPU 并行计算的优势；在矩阵较大时，CPU 的计算时间明显上升，而 GPU 充分发挥并行计算优势，运算时间几乎不变。

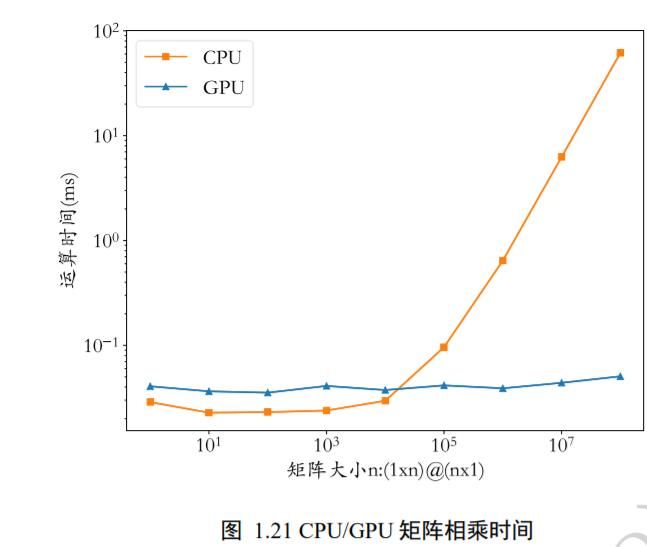
b) 自动梯度
在使用 TensorFlow 构建前向计算过程的时候，除了能够获得数值结果，TensorFlow 还会自动构建计算图，通过 TensorFlow 提供的自动求导的功能，可以不需要手动推导，即可计算出输出对网络的偏导数。
$\begin{array}{c} \mathrm{y}=\mathrm{a} * \mathrm{w}^{2}+\mathrm{b} * \mathrm{w}+\mathrm{c} \\ \frac{d y}{d w}=2 a w+b \end{array}$
考虑在(a,b,c,w)=(1,2,3,4)处的导数， $\frac{d y}{d w}=2 * 1 * 4+2=10$
通过Tensorflow实现如下

import tensorflow as tf
# 创建4个张量
a=tf.constant(1.)
b=tf.constant(2.)
c=tf.constant(3.)
w=tf.constant(4.)

with tf.GradientTape() as tape: #构建梯度环境
  tape.watch([w]) # 将w加入梯度跟踪列表
  # 构建计算过程
  y=a*w**2+b*w+c
# 求导
[dy_dw]=tape.gradient(y,[w])
print(dy_dw) # 打印出导数
tf.Tensor(10.0, shape=(), dtype=float32)

c) 常用神经网络接口
TensorFlow 除了提供底层的矩阵相乘，相加等运算函数，还内建了常用网络运算函数，常用网络层，网络训练，网络保存与加载，网络部署等一系列深度学习系统的便捷功能。使用 TensorFlow 开发网络，可以方便地利用这些功能完成常用业务流程，高效稳定。

1.6 开发环境安装

在领略完深度学习框架所带来的的便利后，我们来着手在本地计算机环境安装TensorFlow 最新版框架。TensorFlow 框架支持多种常见的操作系统，如 Windows 10,Ubuntu 18.04, Mac OS 等等，同时也支持运行在 NVIDIA 显卡上的 GPU 版本和仅适用 CPU完成计算的 CPU 版本。我们以最为常见的 Windows 10 系统，NVIDIA GPU，Python 语言环境为例，介绍如何安装 TensorFlow 框架及其他开发软件等。

一般来说，开发环境安装分为 4 大步骤：安装 Python 解释器 Anaconda，安装 CUDA加速库，安装 TensorFlow 框架，安装常用编辑器。

1.6.1 Anaconda 安装

Python 解释器是让 Python 语言编写的代码能够被 CPU 执行的桥梁，是 Python 语言的核心。用户可以从官网下载最新版本(Python 3.8)的解释器，像普通的应用软件一样安装完成后，就可以调用 python.exe 程序执行 Python 语言编写的源代码文件(*.py)。

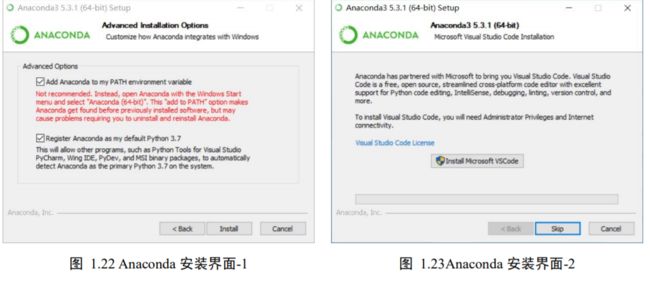
我们这里选择安装集成了 Python 解释器和虚拟环境等一系列辅助功能的 Anaconda 软件，通过安装 Anaconda 软件，可以同时获得 Python 解释器，包管理，虚拟环境等一系列便捷功能，何乐而不为呢。我们从网址进入 Anaconda 下载页面，选择 Python 最新版本的下载链接即可下载，下载完成后安装即可进入安装程序。如图 1.22 所示，勾选”Add Anaconda to my PATH environmentvariable”一项，这样可以通过命令行方式调用 Anaconda 的程序。如图 1.23 所示，安装程序询问是否连带安装 VS Code软件，选择skip即可。整个安装流程持续5~10分钟，具体时间需依据计算机性能而定。

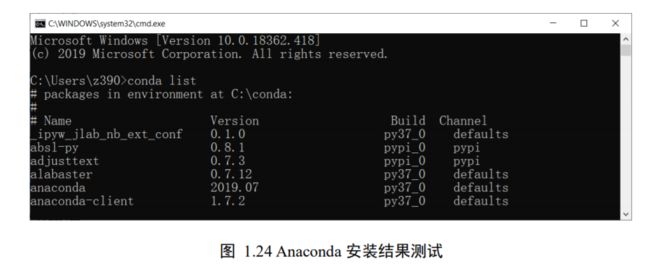
安装完成后，怎么验证 Anaconda 是否安装成功呢？通过键盘上的 Windows 键+R 键，即可调出运行程序对话框，输入 cmd 回车即打开 Windows 自带的命令行程序 cmd.exe，或者点击开始菜单，输入 cmd 也可搜索到 cmd.exe 程序，打开即可。输入 conda list 命令即可查看Python 环境已安装的库，如果是新安装的 Python 环境，则列出的库都是 Anaconda 自带已默认安装的软件库，如图 1.24 所示。如果 conda list 能够正常弹出一系列的库列表信息，说明 Anaconda 软件安装成功，如果 conda 命名不能被识别，则说明安装失败，需要重新安装。

1.6.2 CUDA 安装

目前的深度学习框架大都基于 NVIDIA 的 GPU 显卡进行加速运算，因此需要安装NVIDIA 提供的 GPU 加速库 CUDA 程序。在安装 CUDA 之前，请确认本地计算机具有支持 CUDA 程序的 NVIDIA 显卡设备，如果计算机没有 NVIDIA 显卡，如部分计算机显卡生产商为 AMD，以及部分 MacBook 笔记本电脑，则无法安装 CUDA 程序，因此可以跳过这一步，直接进入 TensorFlow 安装。CUDA 的安装分为 CUDA 软件的安装、cuDNN 深度神经网络加速库的安装和环境变量配置三个步骤，安装稍微繁琐，请读者在操作时思考每个步骤的原因，避免死记硬背流程。

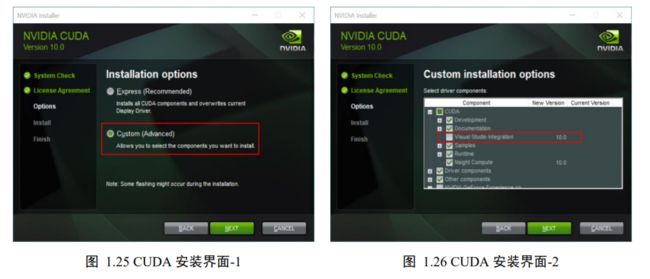
CUDA 软件安装 打开 CUDA 程序的下载官网：https://developer.nvidia.com/cuda-10.0-download-archive，这里我们使用 CUDA 10.0 版本，依次选择 Windows 平台，x86_64 架构，10 系统，exe(local)本地安装包，再选择 Download 即可下载 CUDA 安装软件。下载完成后，打开安装软件。如图 1.25 所示，选择”Custom”选项，点击 NEXT 按钮进入图 1.26安装程序选择列表，在这里选择需要安装和取消不需要安装的程序。在 CUDA 节点下，取消”Visual Studio Integration”一项；在“Driver components”节点下，比对目前计算机已经安装的显卡驱动“Display Driver”的版本号“Current Version”和 CUDA 自带的显卡驱动版本号“New Version”，如果“Current Version”大于“New Version”，则需要取消“Display Driver”的勾，如果小于或等于，则默认勾选即可。设置完成后即可正常安装完成。

安装完成后，我们来测试 CUDA 软件是否安装成功。打开 cmd 命令行，输入“nvcc -V”，即可打印当前 CUDA 的版本信息，如图 1.29 所示，如果命令无法识别，则说明安装失败。同时我们也可从 CUDA 的安装路径“C:\Program Files\NVIDIA GPU ComputingToolkit\CUDA\v10.0\bin”下找到“nvcc.exe”程序，如图 1.28 所示。

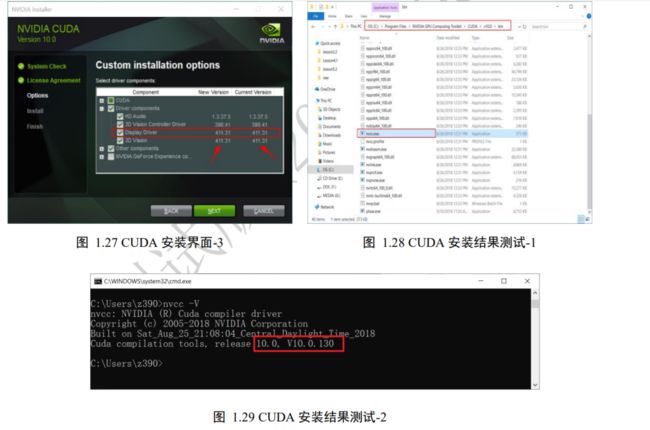
cuDNN 神经网络加速库安装 CUDA 并不是针对于神经网络设计的 GPU 加速库，它面向各种需要并行计算的应用设计。如果希望针对于神经网络应用加速，需要额外安装cuDNN 库。需要注意的是，cuDNN 库并不是运行程序，只需要下载解压 cuDNN 文件，并配置 Path 环境变量即可。

打开网址 https://developer.nvidia.com/cudnn，选择“Download cuDNN”，由于 NVIDIA公司的规定，下载 cuDNN 需要先登录，因此用户需要登录或创建新用户后才能继续下载。登录后，进入 cuDNN 下载界面，勾选“I Agree To the Terms of the cuDNN SoftwareLicense Agreement”，即可弹出 cuDNN 版本下载选项。我们选择 CUDA 10.0 匹配的 cuDNN版本，并点击“cuDNN Library for Windows 10”链接即可下载 cuDNN 文件。需要注意的是，cuDNN 本身具有一个版本号，同时它还需要和 CUDA 的版本号对应上，不能下错不匹配 CUDA 版本号的 cuDNN 文件。

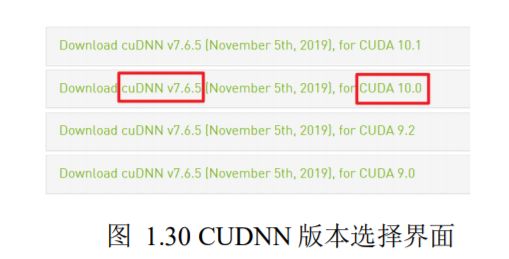
下载完成 cuDNN 文件后，解压并进入文件夹，我们将名为“cuda”的文件夹重命名为“cudnn765”，并复制此文件夹。进入 CUDA 的安装路径 C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.0，粘贴“cudnn765”文件夹即可，此处可能会弹出需要管理员权限的对话框，选择继续即可粘贴，如图 1.31 所示。

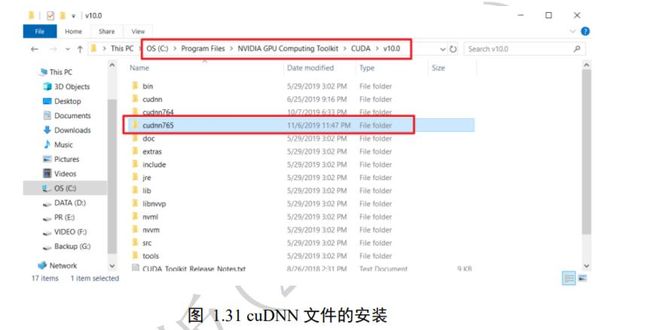
环境变量 Path 配置 上述 cudnn 文件夹的复制即已完成 cuDNN 的安装，但为了让系统能够感知到 cuDNN 文件的位置，我们需要额外配置 Path 环境变量。打开文件浏览器，在“我的电脑”上右击，选择“属性”，选择“高级系统属性”，选择“环境变量”，如图1.32。在“系统变量”一栏中选中“Path”环境变量，选择“编辑”，如图 1.33 所示。选择“新建”，输入我们 cuDNN 的安装路径“C:\Program Files\NVIDIA GPU ComputingToolkit\CUDA\v10.0\cudnn765\bin”，并通过“向上移动”按钮将这一项上移置顶。

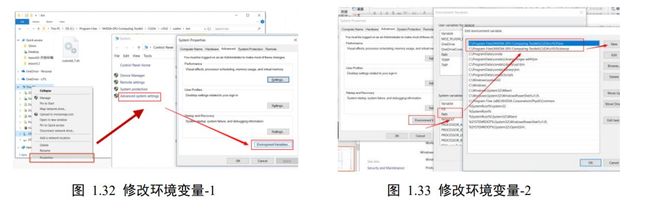
CUDA 安装完成后，环境变量中应该包含“C:\Program Files\NVIDIA GPU ComputingToolkit\CUDA\v10.0\bin”，“C:\Program Files\NVIDIA GPU ComputingToolkit\CUDA\v10.0\libnvvp”和“C:\Program Files\NVIDIA GPU ComputingToolkit\CUDA\v10.0\cudnn765\bin”三项，具体的路径可能依据实际路径略有出入，如图测
1.34 所示，确认无误后依次点击确定，关闭所有对话框。

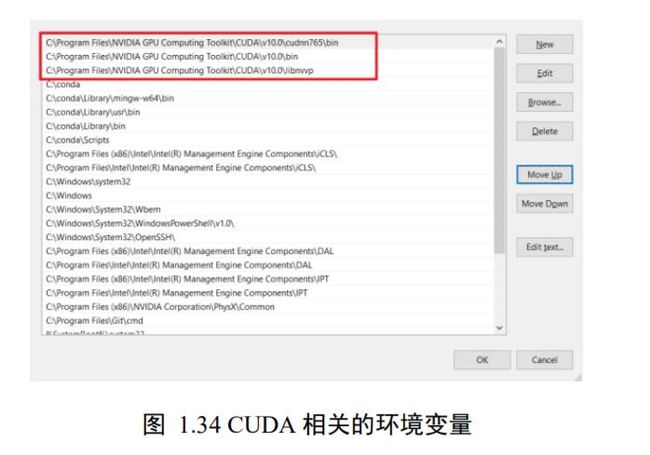
1.6.3 TensorFlow 安装

TensorFlow 和其他的 Python 库一样，使用Python 包管理工具 pip install 命令即可安装。安装 TensorFlow 时，需要根据电脑是否 NVIDIAGPU 显卡来确定是安装性能更强的GPU 版本还是性能一般的 CPU 版本。

国内使用 pip 命令安装时，可能会出现下载速度缓慢甚至连接断开的情况，需要配置国内的 pip 源，只需要在 pip install 命令后面带上“-i 源地址”即可，例如使用清华源安装numpy 包，首先打开 cmd 命令行程序，输入：

# 使用国内清华源安装 numpy
pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple

即可自动下载并按着 numpy 库，配置上国内源的 pip 下载速度会提升显著。现在我们来 TensorFlow GPU 最新版本：

# 使用清华源安装 TensorFlow GPU 版本
pip install -U tensorflow-gpu -i https://pypi.tuna.tsinghua.edu.cn/simple

上述命令自动下载 TensorFlow GPU 版本并安装，目前是 TensorFlow 2.0.0 正式版，“-U”参数指定如果已安装此包，则执行升级命令。

现在我们来测试 GPU 版本的 TensorFlow 是否安装成功。在 cmd 命令行输入 ipython 进入 ipython 交互式终端，输入“import tensorflow as tf”命令，如果没有错误产生，继续输入“tf.test.is_gpu_available()”测试 GPU 是否可用，此命令会打印出一系列以“I”开头的信息(Information)，其中包含了可用的 GPU 显卡设备信息，最后会返回“True”或者“False”，代表了 GPU 设备是否可用，如图 1.35 所示。如果为 True，则 TensorFlow GPU版本安装成功；如果为 False，则安装失败，需要再次检测 CUDA，cuDNN，环境变量等步骤，或者复制错误，从搜索引擎中寻求帮助。

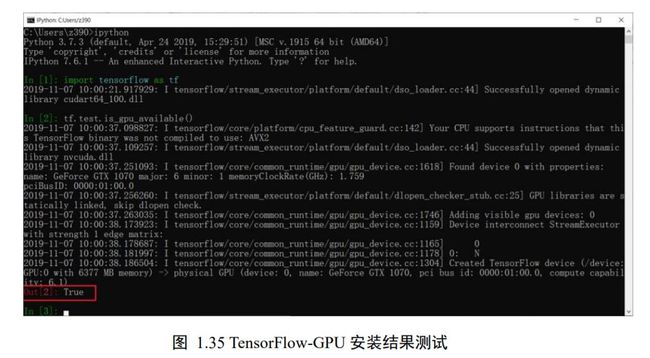
如果不能安装 TensorFlow GPU 版本，则可以安装 CPU 版本暂时用作学习。CPU 版本无法利用 GPU 加速运算，计算速度相对缓慢，但是作为学习介绍的算法模型一般不大，使用 CPU 版本也能勉强应付，待日后对深度学习有了一定了解再升级 NVIDIA GPU 设备也未尝不可。亦或者，安装 TensorFlow GPU 版本可能容易出现安装失败的情况，很多读者朋友动手能力一般，如果折腾了很久还不能搞定，可以直接安装 CPU 版本先使用着。

安装 CPU 版本的命令为：

# 使用国内清华源安装 TensorFlow CPU 版本
pip install -U tensorflow -i https://pypi.tuna.tsinghua.edu.cn/simple

安装完后，在 ipython 中输入“import tensorflow as tf”命令即可验证 CPU 版本是否安装成功。

TensorFlow GPU/CPU 版本安装完成后，可以通过“tf.version”查看本地安装的TensorFlow 版本号，如图 1.36所示

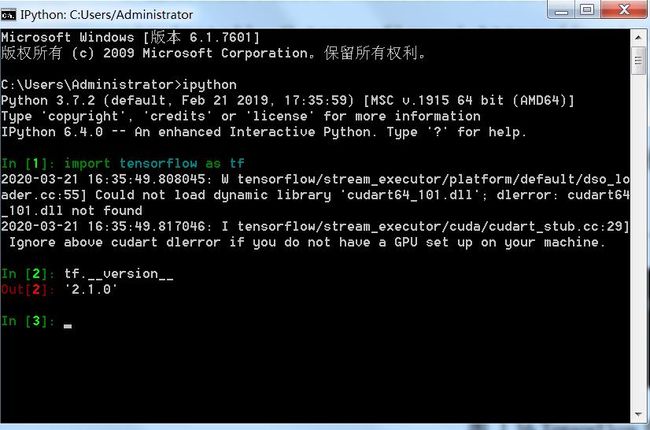
常用的 python 库也可以顺带安装：

# 使用清华源安装常用 python 库
pip install -U numpy matplotlib pillow pandas -i https://pypi.tuna.tsinghua.edu.cn/simple

1.6.4 常用编辑器安装

使用 Python 语言编写程序的方式非常多，可以使用 ipython 或者 ipython notebook 方式交互式编写代码，也可以利用 Sublime Text，PyCharm 和 VS Code 等综合 IDE 开发中大型项目。本书推荐使用 PyCharm 编写和调试，使用 VS Code 交互式开发，这两者都可以免费使用，用户自行下载安装，并配置 Python 解释器，限于篇幅，不再敖述。接下来，让我们开启深度学习之旅吧！

第2章回归问题

有些人担心人工智能会让人类觉得自卑，但是实际上，即使是看到一朵花，我们也应该或多或少感到一些自愧不如。−艾伦·凯

2.1 神经元模型

成年人大脑中包含了约 1000 亿个神经元，每个神经元通过树突获取输入信号，通过轴突传递输出信号，神经元之间相互连接构成了巨大的神经网络，从而形成了人脑的感知和意识基础，图 2.1 是一种典型的生物神经元结构。1943 年，心理学家沃伦·麦卡洛克(Warren McCulloch)和数理逻辑学家沃尔特·皮茨(Walter Pitts)通过对生物神经元的研究，提出了模拟生物神经元机制的人工神经网络的数学模型 (McCulloch & Pitts, 1943)，这一成果被美国神经学家弗兰克·罗森布拉特(Frank Rosenblatt)进一步发展成感知机(Perceptron)模型，这也是现代深度学习的基石。

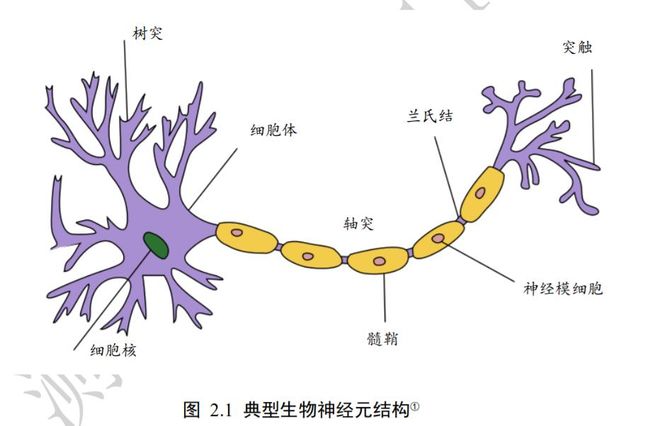
我们将从生物神经元的结构出发，重温科学先驱们的探索之路，逐步揭开自动学习机器的神秘面纱。

首先，我们把生物神经元(Neuron)的模型抽象为如图 2.2(a)所示的数学结构：神经元输入向量 = [1, 2, 3, … , ]T，经过函数映射：: → 后得到输出，其中为函数自身的参数。考虑一种简化的情况，即线性变换：() = T + ，展开为标量形式：
() = 11 + 22 + 33 + ⋯ + +
上述计算逻辑可以通过图 2.2(b)直观地展现

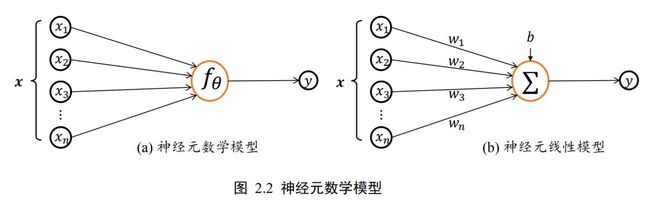
参数 ∶= {1, 2, 3, . . . , ,}确定了神经元的状态，通过固定参数即可确定此神经元的处理逻辑。当神经元输入节点数 = 1(单输入)时，神经元数学模型可进一步简化为： = +

此时我们可以绘制出神经元的输出和输入的变化趋势，如图 2.3 所示，随着输入信号的增加，输出电平也随之线性增加，其中参数可以理解为直线的斜率(Slope)，b 参数为直线的偏置(Bias)。

对于某个神经元来说，和的映射关系 $f_{w,b}$ 是未知但确定的。两点即可确定一条直线，为了估计和的值，我们只需从图 2.3 中直线上采样任意 2 个数据点：
(^{1}, (1)), ((2), (2))即可，其中上标表示数据点编号：
(1) = (1) +
(2) = (2) +

当((1),(1)) ≠ ((2),(2))时，通过求解上式便可计算出和的值。考虑某个具体的例子：(1) = 1,
(1) = 1.56 , (2) = 2, (2) = 3. 3, 代入上式中可得：
1.56 = ∙ 1 +
3. 3 = ∙ 2 +

这就是我们初中时代学习过的二元一次方程组，通过消元法可以轻松计算出和的解析解： = 1. 477, = 0.089 。

可以看到，只需要观测两个不同数据点，就可完美求解单输入线性神经元模型的参数，对于输入的现象神经元模型，只需要采样 + 1组不同数据点即可，似乎线性神经元模型可以得到完美解决。那么上述方法存在什么问题呢？考虑对于任何采样点，都有可能存在观测误差，我们假设观测误差变量属于均值为，方差为2的正态分布(NormalDistribution，或高斯分布，Gaussian Distribution)：(,
2)，则采样到的样本符合：
$x+b+\epsilon, \epsilon \sim \mathcal{N}\left(\mu, \sigma^{2}\right)$

一旦引入观测误差后，即使简单如线性模型，如果仅采样两个数据点，可能会带来较大估计偏差。如图 2.4 所示，图中的数据点均带有观测误差，如果基于蓝色矩形块的两个数据点进行估计，则计算出的蓝色虚线与真实橙色直线存在较大偏差。为了减少观测误差引入的估计偏差，可以通过采样多组数据样本集合 = $\left\{\left(x^{(1)}, y^{(1)}\right),\left(x^{(2)}, y^{(2)}\right), \ldots,\left(x^{(n)}, y^{(n)}\right)\right\}$ ，然后找出一条“最好”的直线，使得它尽可能地让所有采样点到该直线的误差(Error，或损失 Loss)之和最小。

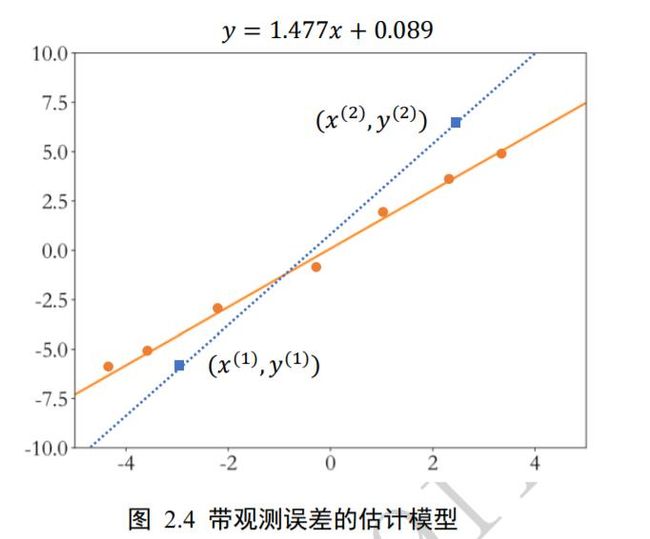
也就是说，由于观测误差的存在，当我们采集了多个数据点时，可能不存在一条直线完美的穿过所有采样点。退而求其次，我们希望能找到一条比较“好”的位于采样点中间的直线。那么怎么衡量“好”与“不好”呢？一个很自然的想法就是，求出当前模型的所有采样点上的预测值() + 与真实值()之间的差的平方和作为总误差ℒ：
$\mathcal{L}=\frac{1}{n} \sum_{i=1}^{n}\left(w x^{(i)}+b-y^{(i)}\right)^{2}$
然后搜索一组参数∗, ∗使得ℒ最小，对应的直线就是我们要寻找的最优直线：
$w^{*}, b^{*}=\underset{w, b}{\operatorname{argmin}} \frac{1}{n} \sum_{i=1}^{n}\left(w x^{(i)}+b-y^{(i)}\right)^{2}$
其中表示采样点的个数。这种误差计算方法称为均方误差(Mean Squared Error，简称
MSE）。

2.2 优化方法

现在来小结一下上述方案：我们需要找出最优参数(Optimal Parameter)∗和∗，使得输入和输出满足线性关系() = () + , ∈ [1, ]。但是由于观测误差的存在，需要通过采样足够多组的数据样本组成的数据集(Dataset)： ={((1),(1)), ((2),(2)),… , ((), ())}，找到一组最优的参数 ∗, ∗使得均方差ℒ =1 (() + − ())2 =1 最小。

对于单输入的神经元模型，只需要两个样本，能通过消元法求出方程组的精确解，这种通过严格的公式推导出的精确解称为解析解(Closed-form Solution)。但是对于多个数据点( ≫ 2)的情况，这时很有可能不存在解析解，我们只能借助数值方法去优化(Optimize)出一个近似的数值解(Numerical Solution)。为什么叫作优化？这是因为计算机的计算速度非常快，我们可以借助强大的计算能力去多次“搜索”和“试错”，从而一步步降低误差ℒ。最简单的优化方法就是暴力搜索或随机试验，比如要找出最合适的w∗和∗，我们就可以从(部分)实数空间中随机采样任意的和，并计算出对应模型的误差值ℒ，然后从测试过的{ℒ}中挑出最好的ℒ∗，它所对应的和就可以作为我们要找的最优w∗和∗。

这种算法固然简单直接，但是面对大规模、高维度数据的优化问题时计算效率极低，基本不可行。梯度下降算法(Gradient Descent)是神经网络训练中最常用的优化算法，配合强大的图形处理芯片 GPU(Graphics Processing Unit)的并行加速能力，非常适合优化海量数据的神经网络模型，自然也适合优化我们这里的神经元线性模型。这里先简单地应用梯度下降算法，用于解决神经元模型预测的问题。由于梯度下降算法是深度学习的核心算法，我们将在第 7 章非常详尽地推导梯度下降算法在神经网络中的应用，这里先给读者第一印象。

我们在高中时代学过导数(Derivative)的概念，如果要求解一个函数的极大、极小值，可以简单地令导数函数为 0，求出对应的自变量点(称为驻点)，再检验驻点类型即可。以函数() = $x^{(2)}$ ∙ ()为例，我们绘制出函数及其导数在 ∈ [−1 ,1 ]区间曲线，其中蓝色实线为()，黄色虚线为 $\frac{\mathrm{d} f(x)}{\mathrm{d} x}$ ，如图 2.5 所示。可以看出，函数导数(虚线)为 0 的点即为()的驻点，函数的极大值和极小值点均出现在驻点中。

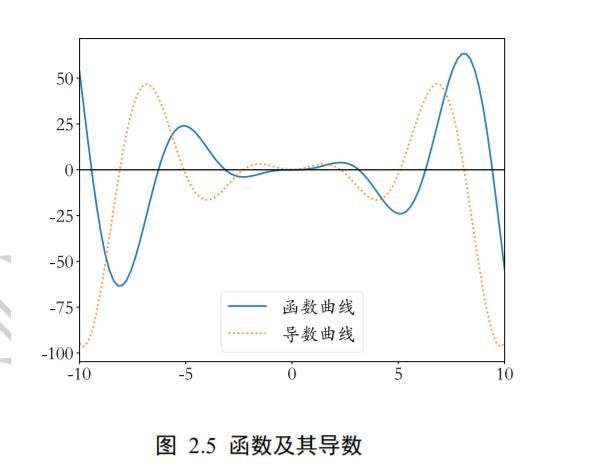
函数的梯度(Gradient)定义为函数对各个自变量的偏导数(Partial Derivative)组成的向量。考虑 3 维函数 = (, )，函数对自变量的偏导数记为 $\frac{\partial z}{\partial x}$ ，函数对自变量y的偏导数记为 $\frac{\partial z}{\partial y}$ ，则梯度∇为向量 $\left(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\right)$ 。我们通过一个具体的函数来感受梯度的性质，如图 2.6所示， $y)=-\left(\cos ^{2} x+\cos ^{2} y\right)^{2}$ ，图中平面的红色箭头的长度表示梯度向量的模，箭头的方向表示梯度向量的方向。可以看到，箭头的方向总是指向当前位置函数值增速最大的方向，函数曲面越陡峭，箭头的长度也就越长，梯度的模也越大。

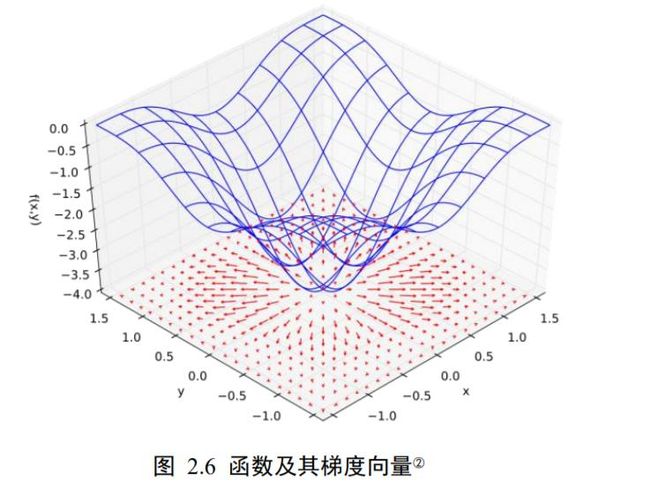
通过上面的例子，我们能直观地感受到，函数在各处的梯度方向∇总是指向函数值增大的方向，那么梯度的反方向−∇应指向函数值减少的方向。利用这一性质，我们只需要按照
$x^{\prime}=x-\eta \cdot \nabla f$
来迭代更新′，就能获得越来越小的函数值，其中用来缩放梯度向量，一般设置为某较小的值，如 0.01，0.001 等。特别地，对于一维函数，上述向量形式可以退化成标量形式：
$x^{\prime}=x-\eta \cdot \frac{\mathrm{d} y}{\mathrm{d} x}$
通过上式迭代更新′若干次，这样得到的′处的函数值′，总是更有可能比在处的函数值小。

通过上面公式优化参数的方法称为梯度下降算法，它通过循环计算函数的梯度∇并更新待优化参数，从而得到函数获得极小值时参数的最优数值解。需要注意的是，在深度学习中，一般表示模型输入，模型的待优化参数一般用、、等符号表示。

现在我们将应用速学的梯度下降算法来求解∗和∗参数。这里要最小化的是均方差误差函数ℒ：
$\mathcal{L}=\frac{1}{n} \sum_{i=0}^{n}\left(w x^{(i)}+b-y^{(i)}\right)^{2}$
需要优化的模型参数是和，因此我们按照
$\begin{array}{l} w^{\prime}=w-\eta \frac{\partial \mathcal{L}}{\partial w} \\ b^{\prime}=b-\eta \frac{\partial \mathcal{L}}{\partial b} \end{array}$
方式循环更新参数。

2.3 线性模型实战

在介绍了用于优化和的梯度下降算法后，我们来实战训练单输入神经元线性模型。首先我们需要采样自真实模型的多组数据，对于已知真实模型的玩具样例(Toy Example)，我们直接从指定的 = 1.477 , = 0.089 的真实模型中直接采样：
$y = 1.477 * x + 0.089$

1. 采样数据

为了能够很好地模拟真实样本的观测误差，我们给模型添加误差自变量，它采样自均值为 0，方差为 0.01 的高斯分布：
$x+0.089+\epsilon, \epsilon \sim \mathcal{N}(0,0.01)$
通过随机采样 = 100 次，我们获得个样本的训练数据集train：

import numpy as np
data=[] #保存样本集的列表
for i in range(100): #循环采样100个点
  x=np.random.uniform(-10.,10.) #随机采样输入x
  # 采样高斯噪声
  eps=np.random.normal(0.,0.1) # 均值和方差
  # 得到模型的输出
  y=1.477*x+0.089+eps
  data.append([x,y]) #保存样本点
data=np.array(data)# 转换为2D Numpy数组
print(data)

循环进行 100 次采样，每次从区间[-10, 10]的均匀分布U( ,1)中随机采样一个数据，同时从均值为 0，方差为 $0.1^{2}$ 的高斯分布( 0, $0.1^{2}$ )中随机采样噪声，根据真实模型生成的数据，并保存为 Numpy数组。

2. 计算误差
循环计算在每个点((), ())处的预测值与真实值之间差的平方并累加，从而获得训练集上的均方差损失值.

def mse(b,w,points):
  totalError=0  # 根据当前的w，b参数计算均方差损失
  for i in range(0,len(points)): # 循环迭代所有点
    x=points[i,0] #获得i号点的输入x
    y=points[i,1]  #获得i号点的输出y
    # 计算差的平方，并累加
    totalError+=(y-(w*x+b))**2
  # 将累加的误差求平均，得到均方误差
  return totalError/float(len(points))

最后的误差和除以数据样本总数，从而得到每个样本上的平均误差。

3. 计算梯度

根据之前介绍的梯度下降算法，我们需要计算出函数在每一个点上的梯度信息： $\left(\frac{\partial \mathcal{L}}{\partial w}, \frac{\partial \mathcal{L}}{\partial b}\right)$ 。我们来推导一下梯度的表达式，首先考虑 $\frac{\partial \mathcal{L}}{\partial w}$ ，将均方差函数展开：
$\frac{\partial \mathcal{L}}{\partial w}=\frac{\partial \frac{1}{n} \sum_{i=1}^{n}\left(w x^{(i)}+b-y^{(i)}\right)^{2}}{\partial w}=\frac{1}{n} \sum_{i=1}^{n} \frac{\partial\left(w x^{(i)}+b-y^{(i)}\right)^{2}}{\partial w}$
考虑到
$\frac{\partial g^{2}}{\partial w}=2 \cdot g \cdot \frac{\partial g}{\partial w}$
因此

如果难以理解上述推导，可以复习数学中函数的梯度相关课程，同时在本书第 7 章也会详细介绍，我们可以记住 $\frac{\partial \mathcal{L}}{\partial w}$ 的最终表达式即可。用同样的方法，我们可以推导偏导数 $\frac{\partial \mathcal{L}}{\partial b}$ 的表达式：
$\begin{array}{c} \frac{\partial \mathcal{L}}{\partial b}=\frac{\partial \frac{1}{n} \sum_{i=1}^{n}\left(w x^{(i)}+b-y^{(i)}\right)^{2}}{\partial b}=\frac{1}{n} \sum_{i=1}^{n} \frac{\partial\left(w x^{(i)}+b-y^{(i)}\right)^{2}}{\partial b} \\ =\frac{1}{n} \sum_{i=1}^{n} 2\left(w x^{(i)}+b-y^{(i)}\right) \cdot \frac{\partial\left(w x^{(i)}+b-y^{(i)}\right)}{\partial b} \\ =\frac{1}{n} \sum_{i=1}^{n} 2\left(w x^{(i)}+b-y^{(i)}\right) \cdot 1 \\ =\frac{2}{n} \sum_{i=1}^{n}\left(w x^{(i)}+b-y^{(i)}\right) \end{array}$
根据上面偏导数的表达式，我们只需要计算在每一个点上面的(() + − ()) ∙()和(() + − ()
)值，平均后即可得到偏导数 $\frac{\partial \mathcal{L}}{\partial w}$ 和 $\frac{\partial \mathcal{L}}{\partial b}$ 。实现如下：

def step_gradient(b_current,w_current,points,lr):
  # 计算误差函数在所有点上的异数，并更新w，b
  b_gradirnt=0
  w_gradient=0
  M=float(len(points))# 总体样本
  for i in range(0,len(points)):
    x=points[i,0]
    y=points[i,1]
    # 误差函数对b的导数；grad_b=2(wx+b-y)
    b_gradirnt+=(2/M) *((w_current*x+b_current)-y)
    # 误差函数对w的求导：grad_w=2(wx+b-y)*x
    w_gradient=w_gradient+(2/M)*x*((w_current*x+b_current)-y)
  # 根据梯度下降算法更新的 w',b',其中lr为学习率
  new_b=b_current-(lr*b_gradirnt)
  new_w=w_current-(lr*w_gradient)
  return [new_b,new_w]

4. 梯度更新

在计算出误差函数在和处的梯度后，我们可以根据公式来更新和的值。我们把对数据集的所有样本训练一次称为一个 Epoch，共循环迭代 num_iterations 个 Epoch。实现如下：

def gradient_descent(points,starting_b,starting_w,lr,num_iterations):
  # 循环更新w，b多次
  b=starting_b #b的初始值
  w=starting_w #w的初始值
  #根据梯度下降算法更新多次
  for step in range(num_iterations):
    # 计算梯度并跟新一次
    b,w=step_gradient(b,w,np.array(points),lr)
    loss=mse(b,w,points) #计算当前的均方误差，用于监控训练进度
    if step%50==0: #打印误差和实时的w，b值
      print("iteration:{},loss:{},w:{},b:{}".format(step,loss,w,b))
  return [b,w] #返回最后一次的w，b

主训练函数实现如下：

def main():
  # 加载训练数据集，这些数据是通过真实模型添加观测误差采集的到的
  lr=0.01 # 学习率
  initial_b=0 # 初始化b为0
  initial_w=0 # 初始化w为0
  num_iteration=1000
  # 训练优化1000次，返回最优 w*,b*和训练Loss的下降过程
  [b,w],losses=gradient_descent(data,initial_b,initial_w,lr,num_iteration)
  loss=mse(b,w,data)# 计算最优数值w,b的均方误差
  print('Final loss:{},w:{},b:{}'.format(loss,w,b))

经过 1000 的迭代更新后，保存最后的和值，此时的和的值就是我们要找的w∗和∗数值解。运行结果如下：
iteration:0, loss:11.437586448749, w:0.88955725981925, b:0.02661765516748428
iteration:50, loss:0.111323083882350, w:1.48132089048970, b:0.58389075913875
iteration:100, loss:0.02436449474995, w:1.479296279074, b:0.78524532356388
…
iteration:950, loss:0.01097700897880, w:1.478131231919, b:0.901113267769968
Final loss:0.010977008978805611, w:1.4781312318924746, b:0.901113270434582
可以看到，第 100 次迭代时，和的值就已经比较接近真实模型了，更新 1000 次后得到的∗和∗数值解与真实模型的非常接近，训练过程的均方差变化曲线如图 2.7 所示。

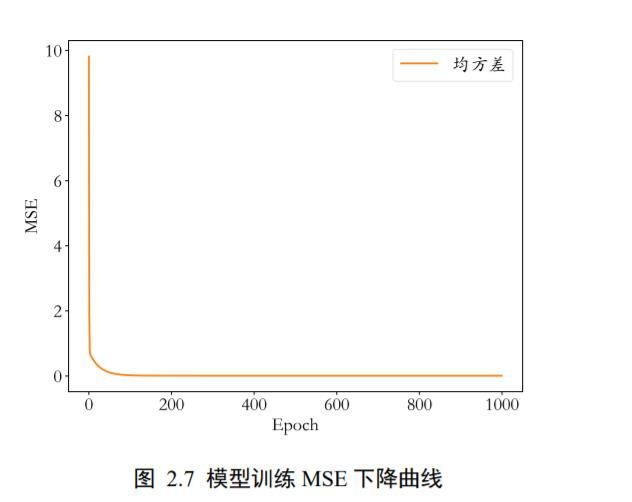
上述例子比较好地展示了梯度下降算法在求解模型参数上的强大之处。需要注意的是，对于复杂的非线性模型，通过梯度下降算法求解到的和可能是局部极小值而非全局最小值解，这是由模型函数的非凸性决定的。但是我们在实践中发现，通过梯度下降算法求得的数值解，它的性能往往都能优化得很好，可以直接使用求解到的数值解和来近似作为最优解。

2.4 线性回归

简单回顾一下我们的探索之路：首先假设个输入的生物神经元的数学模型为线性模型之后，只采样 + 1个数据点就可以估计线性模型的参数和。引入观测误差后，通过梯度下降算法，我们可以采样多组数据点循环优化得到和的数值解。

如果我们换一个角度来看待这个问题，它其实可以理解为一组连续值(向量)的预测问题。给定数据集，我们需要从中学习到数据的真实模型，从而预测未见过的样本的输出值。在假定模型的类型后，学习过程就变成了搜索模型参数的问题，比如我们假设神经元为线性模型，那么训练过程即为搜索线性模型的和参数的过程。训练完成后，利用学到的模型，对于任意的新输入，我们就可以使用学习模型输出值作为真实值的近似。从这个角度来看，它就是一个连续值的预测问题。

在现实生活中，连续值预测问题是非常常见的，比如股价的走势预测、天气预报中温度和湿度等的预测、年龄的预测、交通流量的预测等。对于预测值是连续的实数范围，或者属于某一段连续的实数区间，我们把这种问题称为回归(Regression)问题。特别地，如果使用线性模型去逼近真实模型，那么我们把这一类方法叫做线性回归(Linear Regression，简称 LR)，线性回归是回归问题中的一种具体的实现。

除了连续值预测问题以外，是不是还有离散值预测问题呢？比如说硬币正反面的预测，它的预测值只可能有正面或反面两种可能；再比如说给定一张图片，这张图片中物体的类别也只可能是像猫、狗、天空之类的离散类别值。对于这一类问题，我们把它称为分类(Classification)问题。接下来我们来挑战分类问题吧！

第3章分类问题

在人工智能上花一年时间，这足以让人相信上帝的存在。−艾伦·佩利

前面已经介绍了用于连续值预测的线性回归模型，现在我们来挑战分类问题。分类问题的一个典型应用就是教会机器如何去自动识别图片中物体的种类。考虑图片分类中最简单的任务之一：0~9 数字图片识别，它相对简单，而且也具有非常广泛的应用价值，比如邮政编码、快递单号、手机号码等都属于数字图片识别范畴。我们将以数字图片识别为例，探索如何用机器学习的方法去解决这个问题。

3.1 手写数字图片数据集

机器学习需要从数据中间学习，首先我们需要采集大量的真实样本数据。以手写的数字图片识别为例，如图 3.1 所示，我们需要收集大量的由真人书写的 0~9的数字图片，为了便于存储和计算，一般把收集的原始图片缩放到某个固定的大小(Size 或 Shape)，比如224 个像素的行和 224 个像素的列(224 × 224)，或者 96 个像素的行和 96 个像素的列(96 × 96)，这张图片将作为输入数据 x。同时，我们需要给每一张图片标注一个标签(Label)，它将作为图片的真实值，这个标签表明这张图片属于哪一个具体的类别，一般通过映射方式将类别名一一对应到从 0 开始编号的数字，比如说硬币的正反面，我们可以用0 来表示硬币的反面，用 1 来表示硬币的正面，当然也可以反过来 1 表示硬币的反面，这种编码方式叫作数字编码(Number Encoding)。对于手写数字图片识别问题，编码更为直观，我们用数字的 0~9 来表示类别名字为 0~9 的图片。

如果希望模型能够在新样本上也能具有良好的表现，即模型泛化能力(GeneralizationAbility)较好，那么我们应该尽可能多地增加数据集的规模和多样性(Variance)，使得我们用于学习的训练数据集与真实的手写数字图片的分布(Ground-truth Distribution)尽可能的逼近，这样在训练数据集上面学到了模型能够很好的用于未见过的手写数字图片的预测。

为了方便业界统一测试和评估算法， (Lecun, Bottou, Bengio, & Haffner, 1998)发布了手写数字图片数据集，命名为 MNIST，它包含了 0~9 共 10 种数字的手写图片，每种数字一共有 7000 张图片，采集自不同书写风格的真实手写图片，一共 70000 张图片。其中 60000张图片作为训练train(Training Set)，用来训练模型，剩下 10000 张图片作为测试集test(Test Set)，用来预测或者测试，训练集和测试集共同组成了整个 MNIST 数据集。

考虑到手写数字图片包含的信息比较简单，每张图片均被缩放到28 × 28的大小，同时只保留了灰度信息，如图 3.2 所示。这些图片由真人书写，包含了如字体大小、书写风格、粗细等丰富的样式，确保这些图片的分布与真实的手写数字图片的分布尽可能的接近，从而保证了模型的泛化能力。

现在我们来看下图片的表示方法。一张图片包含了ℎ行(Height/Row)，列(Width/Column)，每个位置保存了像素(Pixel)值，像素值一般使用 0~255 的整形数值来表达颜色强度信息，例如 0 表示强度最低，255 表示强度最高。如果是彩色图片，则每个像素点包含了 R、G、B 三个通道的强度信息，分别代表红色通道、绿色通道、蓝色通道的颜色强度，所以与灰度图片不同，它的每个像素点使用一个 1 维、长度为 3 的向量(Vector)来表示，向量的 3 个元素依次代表了当前像素点上面的 R、G、B 颜色强值，因此彩色图片需要保存为形状是[ℎ, , 3]的张量(Tensor，可以通俗地理解为 3 维数组)。如果是灰度图片，则使用一个数值来表示灰度强度，例如 0 表示纯黑，255 表示纯白，因此它只需要一个形为[ℎ, ]的二维矩阵(Matrix)来表示一张图片信息(也可以保存为[ℎ, , 1]形状的张量)。图 3.3 演示了内容为 8 的数字图片的矩阵内容，可以看到，图片中黑色的像素用 0 表示，灰度信息用 0~255 表示，图片中灰度越白的像素点，对应矩阵位置中数值也就越大。

目前常用的深度学习框架，如 TensorFlow，PyTorch 等，都可以非常方便的通过数行代码自动下载、管理和加载 MNIST 数据集，不需要我们额外编写代码，使用起来非常方便。我们这里利用TensorFlow 自动在线下载 MNIST 数据集，并转换为 Numpy 数组格式：

import os
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,optimizers,datasets

(x,y),(x_val,y_val)=datasets.mnist.load_data()#60000训练集/10000测试集
x=2*tf.convert_to_tensor(x,dtype=tf.float32)/255-1 #转换为张量，缩放到-1~1 60000*28*28
y=tf.one_hot(y,depth=10)#one-hot编码  60000,10
print(x.shape,y.shape)
train_dataset=tf.data.Dataset.from_tensor_slices((x,y))#构建数据集对象
train_dataset=train_dataset.batch(512)#批量训练

load_data()函数返回两个元组(tuple)对象，第一个是训练集，第二个是测试集，每个 tuple的第一个元素是多个训练图片数据X，第二个元素是训练图片对应的类别数字Y。其中训练集X的大小为(60000,28,28)，代表了 60000 个样本，每个样本由 28 行、28 列构成，由于是灰度图片，故没有 RGB 通道；训练集Y的大小为(60000, )，代表了这 60000 个样本的标签数字，每个样本标签用一个 0~9 的数字表示。测试集 X 的大小为(10000,28,28)，代表了10000 张测试图片，Y 的大小为(10000, )。

从 TensorFlow 中加载的 MNIST 数据图片，数值的范围在[0,255]之间。在机器学习中间，一般希望数据的范围在 0 周围小范围内分布。通过预处理步骤，我们把[0,255]像素范围归一化(Normalize)到[0,1.]区间，再缩放到[−1,1]区间，从而有利于模型的训练。

每一张图片的计算流程是通用的，我们在计算的过程中可以一次进行多张图片的计算，充分利用 CPU 或 GPU 的并行计算能力。一张图片我们用 shape 为[h, w]的矩阵来表示，对于多张图片来说，我们在前面添加一个数量维度(Dimension)，使用 shape 为[, ℎ, ]的张量来表示，其中的代表了 batch size(批量)；多张彩色图片可以使用 shape 为[, ℎ, , ]的张量来表示，其中的表示通道数量(Channel)，彩色图片 = 3。通过 TensorFlow 的Dataset 对象可以方便完成模型的批量训练，只需要调用 batch()函数即可构建带 batch 功能的数据集对象。

3.2 模型构建

回顾我们在回归问题讨论的生物神经元结构。我们把一组长度为 $d_{in}$ 的输入向量 =[1, 2, … , ]简化为单输入标量 x，模型可以表达成 = ∗ + 。如果是多输入、单输出的模型结构的话，我们需要借助于向量形式：
$y=\boldsymbol{w}^{T} \boldsymbol{x}+b=\left[w_{1}, w_{2}, w_{3}, \ldots, w_{d_{i n}}\right] \cdot\left[\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ \ldots \\ x_{d_{i n}} \end{array}\right]+b$
更一般地，通过组合多个多输入、单输出的神经元模型，可以拼成一个多输入、多输出的模型：
$y = W x + b$
其中， $\boldsymbol{x} \in R^{d_{i n}}, \boldsymbol{b} \in R^{d_{o u t}}, \boldsymbol{y} \in R^{d_{o u t}}, W \in R^{d_{o u t} \times d_{i n}}$

对于多输出节点、批量训练方式，我们将模型写成张量形式：
$Y = X @ W + b$
其中 $\in R^{b \times d_{i n}}, \boldsymbol{b} \in R^{d_{o u t}}, \quad Y \in R^{b \times d_{o u t}}, \quad W \in R^{d_{i n} \times d_{o u t}}$ ， $d_{in}$ 表示输入节点数， $d_{out}$ 表示输出节点数；X shape 为[, $d_{in}$ ]，表示个样本的输入数据，每个样本的特征长度为；W的 shape 为[ $d_{in}$ , $d_{out}$ ]，共包含了 $d_{in}$ * $d_{out}$ 个网络参数；偏置向量 shape 为 $d_{out}$ ，每个输出节点上均添加一个偏置值；@符号表示矩阵相乘(Matrix Multiplication，matmul)。

考虑 2 个样本，输入特征长度 $d_{in}$ = 3，输出特征长度 $d_{out}$ = 2的模型，公式展开为
$\left[\begin{array}{cc} o_{1}^{1} & o_{2}^{1} \\ o_{1}^{2} & o_{2}^{2} \end{array}\right]=\left[\begin{array}{ccc} x_{1}^{1} & x_{2}^{1} & x_{3}^{1} \\ x_{1}^{2} & x_{2}^{2} & x_{3}^{2} \end{array}\right]\left[\begin{array}{cc} w_{11} & w_{12} \\ w_{21} & w_{22} \\ w_{31} & w_{32} \end{array}\right]+\left[\begin{array}{c} b_{1} \\ b_{2} \end{array}\right]$
其中 $x_{1}^{1}$ , $o_{0}^{0}$ 等符号的上标表示样本索引号，下标表示样本向量的元素。对应模型结构图为

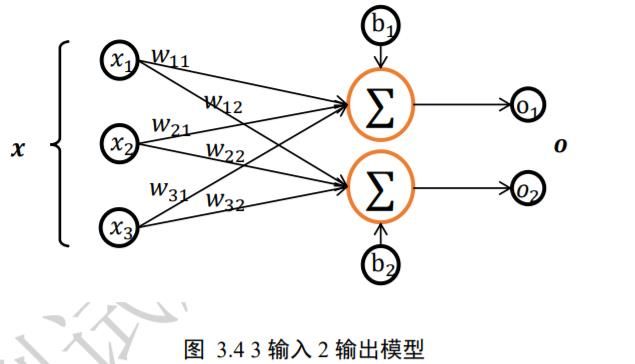
可以看到，通过张量形式表达网络结构，更加简洁清晰，同时也可充分利用张量计算的并行加速能力。那么怎么将图片识别任务的输入和输出转变为满足格式要求的张量形式呢

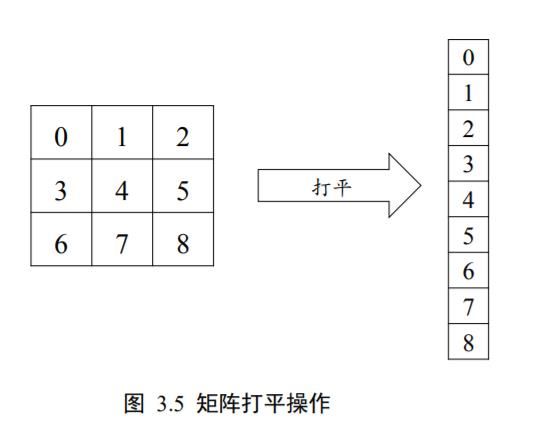
考虑输入格式，一张图片使用矩阵方式存储，shape 为：[ℎ, ]，张图片使用 shape为[, ℎ, ]的张量 X 存储。而我们模型只能接受向量形式的输入特征向量，因此需要将[ℎ, ]的矩阵形式图片特征平铺成[ℎ ∗ ]长度的向量，如图 3.5 所示，其中输入特征的长度 $d_{in}$ = ℎ ∗ 。

对于输出标签，前面我们已经介绍了数字编码，它可以用一个数字来表示便签信息，例如数字 1 表示猫，数字 3 表示鱼等。但是数字编码一个最大的问题是，数字之间存在天然的大小关系，比如1 < 2 < 3，如果 1、2、3 分别对应的标签是猫、狗、鱼，他们之间并没有大小关系，所以采用数字编码的时候会迫使模型去学习到这种不必要的约束。

那么怎么解决这个问题呢？可以将输出设置为 $d_{out}$ 个输出节点的向量， $d_{out}$ 与类别数相同，让第 ∈ [1, $d_{out}$ ]个输出值表示当前样本属于类别的概率(属于类别|)。我们只考虑输入图片只输入一个类别的情况，此时输入图片的真实的标注已经明确：如果物体属于第类的话，那么索引为的位置上设置为 1，其他位置设置为 0，我们把这种编码方式叫做 one-hot 编码(独热编码)。以图 3.6 中的“猫狗鱼鸟”识别系统为例，所有的样本只属于“猫狗鱼鸟”4 个类别中其一，我们将第1,2,3,4号索引位置分别表示猫狗鱼鸟的类别，对于所有猫的图片，它的数字编码为 0，One-hot 编码为[1,0,0,0]；对于所有狗的图片，它的数字编码为 1，One-hot 编码为[0,1,0,0]，以此类推。

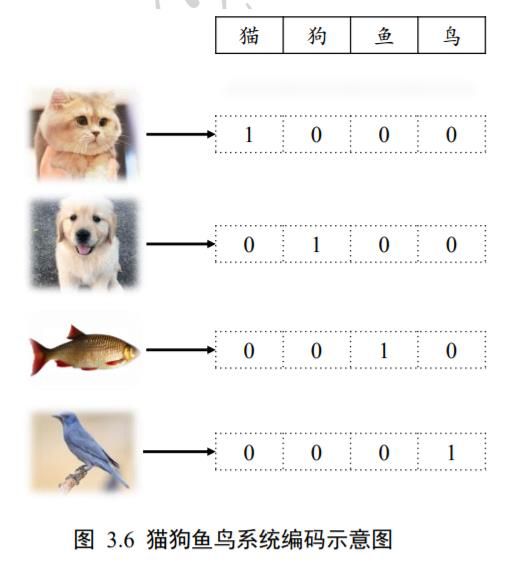
手写数字图片的总类别数有 10 种，即输出节点数 $d_{out}$ = 10，那么对于某个样本，假设它属于类别，即图片的中数字为，只需要一个长度为 10 的向量，向量的索引号为的元素设置为 1，其他位为 0。比如图片 0 的 One-hot 编码为[1,0,0,… ,0]，图片 2 的 Onehot 编码为[0,0,1,… ,0]，图片 9 的One-hot 编码为[0,0,0, … ,1]。One-hot 编码是非常稀疏(Sparse)的，相对于数字编码来说，占用较多的存储空间，所以一般在存储时还是采用数字编码，在计算时，根据需要来把数字编码转换成 One-hot 编码，通过 tf.one_hot即可实现

y=tf.constant([0,1,2,3])#数字编码
y=tf.one_hot(y,depth=10)#one-hot编码
print(y)

tf.Tensor(
[[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]], shape=(4, 10), dtype=float32)

现在我们回到手写数字图片识别任务，输入是一张打平后的图片向量 ∈ R $^{28∗28}$ ，输出
是一个长度为 10 的向量 ∈ $R^{10}$ ，图片的真实标签 y 经过 one-hot 编码后变成长度为 10 的非 0 即 1 的稀疏向量 $\in\{0,1\}^{10}$ 。预测模型采用多输入、多输出的线性模型 = + ，其中模型的输出记为输入的预测值，我们希望越接近真实标签越好。我们一般把输入经过一次(线性)变换叫做一层网络。

3.3 误差计算

对于分类问题来说，我们的目标是最大化某个性能指标，比如准确度 acc，但是把准确度当做损失函数去优化时，会发现 $\frac{\partial a c c}{\partial \theta}$ 是不可导的，无法利用梯度下降算法优化网络参数。一般的做法是，设立一个平滑可导的代理目标函数，比如优化模型的输出与 Onehot 编码后的真实标签之间的距离(Distance)，通过优化代理目标函数得到的模型，一般在测试性能上也能有良好的表现。因此，相对回归问题而言，分类问题的优化目标函数和评价目标函数是不一致的。模型的训练目标是通过优化损失函数ℒ来找到最优数值解W∗, ∗:
$\mathrm{W}^{*}, \boldsymbol{b}^{*}=\underbrace{\underset{W, \boldsymbol{b}}{\operatorname{argmin}} \mathcal{L}(\boldsymbol{o}, \boldsymbol{y})}$
对于分类问题的误差计算来说，更常见的是采用****交叉熵(Cross entropy)损失函数，而不是采用回归问题中介绍的均方差损失函数。我们将在后续章节介绍交叉熵损失函数，这里还是采用 MSE 损失函数来求解手写数字识别问题。对于个样本的均方差损失函数可以表达为：
$\mathcal{L}(\boldsymbol{o}, \boldsymbol{y})=\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{10}\left(o_{j}^{i}-y_{j}^{i}\right)^{2}$
现在我们只需要采用梯度下降算法来优化损失函数得到W, 的最优解，利用求得的模型去预测未知的手写数字图片 ∈ 。

3.4 真的解决了吗

按照上面的方案，手写数字图片识别问题真的得到了完美的解决吗？目前来看，至少存在两大问题：

❑ 线性模型 线性模型是机器学习中间最简单的数学模型之一，参数量少，计算简单，但是只能表达线性关系。即使是简单如数字图片识别任务，它也是属于图片识别的范畴，人类目前对于复杂大脑的感知和决策的研究尚处于初步探索阶段，如果只使用一个简单的线性模型去逼近复杂的人脑图片识别模型，很显然不能胜任

❑ 表达能力 上面的解决方案只使用了少量神经元组成的一层网络模型，相对于人脑中千亿级别的神经元互联结构，它的表达能力明显偏弱，其中表达能力体现为逼近复杂分布的能力

模型的表达能力与数据模态之间的示意图如图 3.7 所示，图中绘制了带观测误差的采样点的分布，人为推测数据的真实分布可能是某 2 次抛物线模型。如图 3.7(a)所示，如果使用表达能力偏弱的线性模型去学习，很难学习到比较好的模型；如果使用合适的多项式函数模型去学习，则能学到比较合适的模型，如图 3.7(b)；但模型过于复杂，表达能力过强时，则很有可能会过拟合，伤害模型的泛化能力，如图 3.7©。

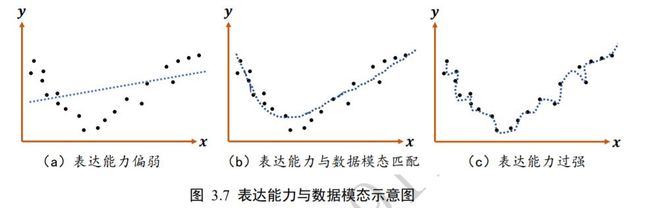
目前我们所采用的多神经元模型仍是线性模型，表达能力偏弱，接下来我们尝试解决这 2个问题。

3.5 非线性模型

既然线性模型不可行，我们可以给线性模型嵌套一个非线性函数，即可将其转换为非线性模型。我们把这个非线性函数称为激活函数(Activation function)，用表示：
$\boldsymbol{o}=\sigma(\boldsymbol{W} \boldsymbol{x}+\boldsymbol{b})$
这里的代表了某个具体的非线性激活函数，比如 Sigmoid 函数(图 3.8(a))，ReLU 函数(图3.8(b))。

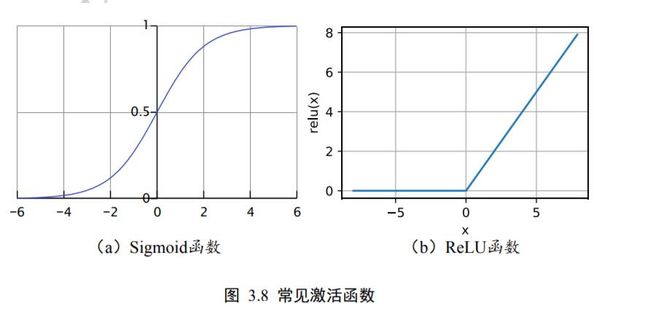
ReLU 函数非常简单，仅仅是在 = 在基础上面截去了 < 0的部分，可以直观地理解为 ReLU 函数仅仅保留正的输入部份，清零负的输入。虽然简单，ReLU 函数却有优良的非线性特性，而且梯度计算简单，训练稳定，是深度学习模型使用最广泛的激活函数之一。我们这里通过嵌套 ReLU 函数将模型转换为非线性模型：
$\boldsymbol{o}=\operatorname{ReLU}(\boldsymbol{W} \boldsymbol{x}+\boldsymbol{b})$

3.6 表达能力

针对于模型的表达能力偏弱的问题，可以通过重复堆叠多次变换来增加其表达能力：
= ( + )
= ( + )
$\boldsymbol{o}$ = +

把第一层神经元的输出值作为第二层神经元模型的输入，把第二层神经元的输出作为第三层神经元的输入，最后一层神经元的输出作为模型的输出。

从网络结构上看，如图 3.9 所示，函数的嵌套表现为网络层的前后相连，每堆叠一个(非)线性环节，网络层数增加一层。我们把数据节点所在的层叫做输入层，每一个非线性模块的输出连同它的网络层参数和称为一层网络层，特别地，对于网络中间的层，叫做隐藏层，最后一层叫做输出层。这种由大量神经元模型连接形成的网络结构称为(前馈)神经网络(Neural Network)。

现在我们的网络模型已经升级为为 3 层的神经网络，具有较好的非线性表达能力，接下来我们讨论怎么优化网络。

3.7 优化方法

对于仅一层的网络模型，如线性回归的模型，我们可以直接推导出 $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$ 的表达式，然后直接计算每一步的梯度，根据梯度更新法则循环更新, 参数即可。但是，当网络层数增加、数据特征长度增大、添加复杂的非线性函数之后，模型的表达式将变得非常复杂，很难手动推导出梯度的计算公式；而且一旦网络结构发生变动，网络的函数模型也随之发生改变，依赖人工去计算梯度的方式显然不可行。

这个时候就是深度学习框架发明的意义所在，借助于自动求导(Autograd)技术，深度学习框架在计算函数的损失函数的过程中，会记录模型的计算图模型，并自动完成任意参数的偏导分 $\frac{\partial L}{\partial \theta}$ 的计算，用户只需要搭建出网络结构，梯度将自动完成计算和更新，使用起来非常便捷高效。

3.8 手写数字图片识别体验

本节我们将在未介绍 TensorFlow 的情况下，先带大家体验一下神经网络的乐趣。本节的主要目的并不是教会每个细节，而是让读者对神经网络算法有全面、直观的感受，为接下来介绍 TensorFlow 基础和深度学习理论打下基础。让我们开始体验神奇的图片识别算法吧！

网络搭建 对于第一层模型来说，他接受的输入 ∈ $R^{784}$ ，输出 ∈ $R^{256}$ 设计为长度为 256的向量，我们不需要显式地编写 = ( + )的计算逻辑，在 TensorFlow 中通过一行代码即可实现：

layers.Dense(256, activation='relu')

使用 TensorFlow 的 Sequential 容器可以非常方便地搭建多层的网络。对于 3 层网络，我们可以通过

keras.sequential([
    layers.Dense(256,activation='relu'),
    layers.Dense(128,activation='relu'),
    layers.Dense(10)])

快速完成 3 层网络的搭建，第 1 层的输出节点数设计为 256，第 2 层设计为 128，输出层节点数设计为 10。直接调用这个模型对象 model(x)就可以返回模型最后一层的输出。

模型训练 得到模型输出 $\boldsymbol{o}$ 后，通过 MSE 损失函数计算当前的误差ℒ：

with tf.GradientTape() as tape:#构建梯度记录环境
    #打平，[b,28,28] =>[b,784]
    x=tf.reshape(x,(-1,28*28))
    #step1. 得到模型输出 output
    # [b,784] =>[b,10]
    out=model(x)

再利用 TensorFlow 提供的自动求导函数 tape.gradient(loss, model.trainable_variables)求出模型中所有的梯度信息 $\frac{\partial L}{\partial \theta}$ , ∈ {1, ,2, ,3, }：

# Step3. 计算参数的梯度 w1, w2, w3, b1, b2, b3
 grads = tape.gradient(loss, model.trainable_variables)

计算获得的梯度结果使用 grads 变量保存。再使用 optimizers 对象自动按着梯度更新法则
$\theta^{\prime}=\theta-\eta * \frac{\partial \mathcal{L}}{\partial \theta}$
去更新模型的参数。

grads = tape.gradient(loss, model.trainable_variables)
 # w' = w - lr * grad，更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))

循环迭代多次后，就可以利用学好的模型去预测未知的图片的类别概率分布。模型的测试部分暂不讨论。

手写数字图片 MNIST 数据集的训练误差曲线如图 3.10 所示，由于 3 层的神经网络表达能力较强，手写数字图片识别任务简单，误差值可以较快速、稳定地下降，其中对数据集的所有图片迭代一遍叫做一个 Epoch，我们可以在间隔数个 Epoch 后测试模型的准确率等指标，方便监控模型的训练效果。

3.9 小结

本章我们通过将一层的线性回归模型类推到分类问题，提出了表达能力更强的三层非线性神经网络，去解决手写数字图片识别的问题。本章的内容以感受为主，学习完大家其实已经了解了(浅层)的神经网络算法，接下来我们将学习 TensorFlow 的一些基础知识，为后续正式学习、实现深度学习算法打下夯实的基石。

第4章 TensorFlow 基础

TensorFlow 是一个面向于深度学习算法的科学计算库，内部数据保存在张量(Tensor)对象上，所有的运算操作(Operation, OP)也都是基于张量对象进行。复杂的神经网络算法本质上就是各种张量相乘、相加等基本运算操作的组合，在深入学习深度学习算法之前，熟练掌握 TensorFlow 张量的基础操作方法十分重要。

4.1 数据类型

首先我们来介绍 TensorFlow 中的基本数据类型，它包含了数值型、字符串型和布尔型。

4.1.1 数值类型

数值类型的张量是 TensorFlow 的主要数据载体，分为：

❑ 标量(Scalar) 单个的实数，如 1.2, 3.4 等，维度数(Dimension，也叫秩)为 0，shape 为[]

❑ 向量(Vector) n 个实数的有序集合，通过中括号包裹，如[1.2]，[1.2,3.4]等，维度数为1，长度不定，shape 为[]

❑ 矩阵(Matrix) n 行 m 列实数的有序集合，如[[1,2],[3,4]]，也可以写成
$\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]$
维度数为 2，每个维度上的长度不定，shape 为[, ]

❑ 张量(Tensor) 所有维度数dim > 2的数组统称为张量。张量的每个维度也做轴(Axis)，一般维度代表了具体的物理含义，比如 Shape 为[2,32,32,3]的张量共有 4 维，如果表示图片数据的话，每个维度/轴代表的含义分别是：图片数量、图片高度、图片宽度、图片通道数，其中 2 代表了 2 张图片，32 代表了高宽均为 32，3 代表了 RGB 3 个通道。张量的维度数以及每个维度所代表的具体物理含义需要由用户自行定义

在 TensorFlow 中间，为了表达方便，一般把标量、向量、矩阵也统称为张量，不作区分，需要根据张量的维度数和形状自行判断。

首先来看标量在 TensorFlow 是如何创建的：

a=1.2
aa=tf.constant(1.2)# 创建标量
print(type(a))
print(type(aa))
print(tf.is_tensor(aa))

output:
<class 'float'>
<class 'tensorflow.python.framework.ops.EagerTensor'>
True

必须通过 TensorFlow 规定的方式去创建张量，而不能使用 Python 语言的标准变量创建方式。
通过 print(x)或 x 可以打印出张量 x 的相关信息：

x = tf.constant([1,2.,3.3])

<tf.Tensor: id=165, shape=(3,), dtype=float32, numpy=array([1. , 2. , 3.3],dtype=float32)>

其中 id 是 TensorFlow 中内部索引对象的编号，shape 表示张量的形状，dtype 表示张量的数值精度，张量 numpy()方法可以返回 Numpy.array 类型的数据，方便导出数据到系统的其他模块：

Ix.numpy()

array([1. , 2. , 3.3], dtype=float32)

与标量不同，向量的定义须通过 List 类型传给 tf.constant()。创建一个元素的向量

a = tf.constant([1.2])
a, a.shape

(<tf.Tensor: id=8, shape=(1,), dtype=float32, numpy=array([1.2],dtype=float32)>,TensorShape([1]))

创建 2 个元素的向量：

a = tf.constant([1,2, 3.])
a, a.shape

(<tf.Tensor: id=11, shape=(3,), dtype=float32, numpy=array([1., 2., 3.],dtype=float32)>,TensorShape([3]))

同样的方法定义矩阵：

a = tf.constant([[1,2],[3,4]])
a, a.shape

(<tf.Tensor: id=13, shape=(2, 2), dtype=int32, numpy=array([[1, 2],[3, 4]])>, TensorShape([2, 2]))

3 维张量可以定义为：

a = tf.constant([
[
[1,2],[3,4]],[[5,6],[7,8]
]
])

<tf.Tensor: id=15, shape=(2, 2, 2), dtype=int32, numpy=array([[[1, 2],[3, 4]],[[5, 6],[7, 8]]])>

4.1.2 字符串类型

除了丰富的数值类型外，TensorFlow 还支持字符串(String)类型的数据，例如在表示图片数据时，可以先记录图片的路径，再通过预处理函数根据路径读取图片张量。通过传入字符串对象即可创建字符串类型的张量：

a = tf.constant('Hello, Deep Learning.')

<tf.Tensor: id=17, shape=(), dtype=string, numpy=b'Hello, Deep Learning.'>

在 tf.strings 模块中，提供了常见的字符串型的工具函数，如拼接 join()，长度 length()，切分 split()等等：

tf.strings.lower(a)

<tf.Tensor: id=19, shape=(), dtype=string, numpy=b'hello, deep learning.'>

深度学习算法主要还是以数值类型张量运算为主，字符串类型的数据使用频率较低，我们不做过多阐述。

4.1.3 布尔类型

为了方便表达比较运算操作的结果，TensorFlow 还支持布尔类型(Boolean, bool)的张量。布尔类型的张量只需要传入 Python 语言的布尔类型数据，转换成 TensorFlow 内部布尔型即可：

a = tf.constant(True)

<tf.Tensor: id=22, shape=(), dtype=bool, numpy=True>

传入布尔类型的向量：

a = tf.constant([True, False])

<tf.Tensor: id=25, shape=(2,), dtype=bool, numpy=array([ True, False])>

需要注意的是，TensorFlow 的布尔类型和 Python 语言的布尔类型并不对等，不能通用：

a = tf.constant(True) # 创建布尔张量
a == True

False

4.2 数值精度

对于数值类型的张量，可以保持为不同字节长度的精度，如浮点数 3.14 既可以保存为16-bit 长度，也可以保存为 32-bit 甚至 64-bit 的精度。Bit 位越长，精度越高，同时占用的内存空间也就越大。常用的精度类型有 tf.int16, tf.int32, tf.int64, tf.float16, tf.float32,tf.float64，其中 tf.float64 即为 tf.double。在创建张量时，可以指定张量的保存精度：

tf.constant(123456789, dtype=tf.int16)
tf.constant(123456789, dtype=tf.int32)

<tf.Tensor: id=33, shape=(), dtype=int16, numpy=-13035>
<tf.Tensor: id=35, shape=(), dtype=int32, numpy=123456789>

可以看到，保存精度过低时，数据 123456789 发生了溢出，得到了错误的结果，一般使用tf.int32, tf.int64 精度。对于浮点数，高精度的张量可以表示更精准的数据，例如采用tf.float32 精度保存时：

import numpy as np
np.pi
tf.constant(np.pi, dtype=tf.float32)

<tf.Tensor: id=29, shape=(), dtype=float32, numpy=3.1415927>

如果采用 tf.float32 精度保存，则能获得更高的精度：

tf.constant(np.pi, dtype=tf.float64)

<tf.Tensor: id=31, shape=(), dtype=float64, numpy=3.141592653589793>

对于大部分深度学习算法，一般使用 tf.int32, tf.float32 可满足运算精度要求，部分对精度要求较高的算法，如强化学习，可以选择使用 tf.int64, tf.float64 精度保存张量。

4.2.1 读取精度

通过访问张量的 dtype 成员属性可以判断张量的保存精度：

print('before:',a.dtype)
if a.dtype != tf.float32:
    a = tf.cast(a,tf.float32) # 转换精度
print('after :',a.dtype)

before: <dtype: 'float16'>
after : <dtype: 'float32'>

对于某些只能处理指定精度类型的运算操作，需要提前检验输入张量的精度类型，并将不符合要求的张量进行类型转换。

4.2.2 类型转换

系统的每个模块使用的数据类型、数值精度可能各不相同，对于不符合要求的张量的类型及精度，需要通过 tf.cast 函数进行转换：

a = tf.constant(np.pi, dtype=tf.float16)
tf.cast(a, tf.double)

<tf.Tensor: id=44, shape=(), dtype=float64, numpy=3.140625>

进行类型转换时，需要保证转换操作的合法性，例如将高精度的张量转换为低精度的张量
时，可能发生数据溢出隐患：

a = tf.constant(123456789, dtype=tf.int32)
tf.cast(a, tf.int16)

<tf.Tensor: id=38, shape=(), dtype=int16, numpy=-13035>

布尔型与整形之间相互转换也是合法的，是比较常见的操作：

a = tf.constant([True, False])
tf.cast(a, tf.int32)

<tf.Tensor: id=48, shape=(2,), dtype=int32, numpy=array([1, 0])>

一般默认 0 表示 False，1 表示 True，在 TensorFlow 中，将非 0 数字都视为 True:

a = tf.constant([-1, 0, 1, 2])
tf.cast(a, tf.bool)

<tf.Tensor: id=51, shape=(4,), dtype=bool, numpy=array([ True, False, True,True])>

4.3 待优化张量

为了区分需要计算梯度信息的张量与不需要计算梯度信息的张量，TensorFlow 增加了一种专门的数据类型来支持梯度信息的记录：tf.Variable。tf.Variable 类型在普通的张量类型基础上添加了 name，trainable 等属性来支持计算图的构建。由于梯度运算会消耗大量的计算资源，而且会自动更新相关参数，对于不需要的优化的张量，如神经网络的输入 X，不需要通过 tf.Variable 封装；相反，对于需要计算梯度并优化的张量，如神经网络层的W和，需要通过 tf.Variable 包裹以便 TensorFlow 跟踪相关梯度信息。

通过 tf.Variable()函数可以将普通张量转换为待优化张量：

a = tf.constant([-1, 0, 1, 2])
aa = tf.Variable(a)
aa.name, aa.trainable

('Variable:0', True)

其中张量的 name 和 trainable 属性是 Variable 特有的属性，name 属性用于命名计算图中的变量，这套命名体系是 TensorFlow 内部维护的，一般不需要用户关注 name 属性；trainable表征当前张量是否需要被优化，创建 Variable 对象是默认启用优化标志，可以设置trainable=False 来设置张量不需要优化。

除了通过普通张量方式创建 Variable，也可以直接创建：

a = tf.Variable([[1,2],[3,4]])

<tf.Variable 'Variable:0' shape=(2, 2) dtype=int32, numpy=array([[1, 2],[3, 4]])>

待优化张量可看做普通张量的特殊类型，普通张量也可以通过 GradientTape.watch()方法临时加入跟踪梯度信息的列表。

4.4 创建张量

在 TensorFlow 中，可以通过多种方式创建张量，如从 Python List 对象创建，从Numpy 数组创建，或者创建采样自某种已知分布的张量等。

4.4.1 从 Numpy, List 对象创建

Numpy Array 数组和 Python List 是 Python 程序中间非常重要的数据载体容器，很多数据都是通过 Python 语言将数据加载至 Array 或者 List 容器，再转换到 Tensor 类型，通过TensorFlow 运算处理后导出到 Array 或者 List 容器，方便其他模块调用。

通过 tf.convert_to_tensor 可以创建新 Tensor，并将保存在 Python List 对象或者 Numpy Array 对象中的数据导入到新 Tensor 中：

tf.convert_to_tensor([1,2.])

<tf.Tensor: id=86, shape=(2,), dtype=float32, numpy=array([1., 2.],dtype=float32)>

tf.convert_to_tensor(np.array([[1,2.],[3,4]]))

<tf.Tensor: id=88, shape=(2, 2), dtype=float64, numpy=array([[1., 2.], [3., 4.]])>

需要注意的是，Numpy 中浮点数数组默认使用 64-Bit 精度保存数据，转换到 Tensor 类型时精度为 tf.float64，可以在需要的时候转换为 tf.float32 类型。

实际上，tf.constant()和 tf.convert_to_tensor()都能够自动的把 Numpy 数组或者 PythonList 数据类型转化为 Tensor 类型，这两个 API 命名来自 TensorFlow 1.x 的命名习惯，在TensorFlow 2 中函数的名字并不是很贴切，使用其一即可.

4.4.2 创建全 0，全 1 张量

将张量创建为全 0 或者全 1 数据是非常常见的张量初始化手段。考虑线性变换 = + ，将权值矩阵 W 初始化为全 1 矩阵，偏置 b 初始化为全 0 向量，此时线性变化层输出 = ，是一种比较好的层初始化状态。

通过 tf.zeros()和 tf.ones()即可创建任意形状全 0 或全 1 的张量。例如，创建为 0 和为 1 的标量张量：

tf.zeros([]),tf.ones([])

(<tf.Tensor: id=90, shape=(), dtype=float32, numpy=0.0>,
<tf.Tensor: id=91, shape=(), dtype=float32, numpy=1.0>)

创建全 0 和全 1 的向量：

tf.zeros([1]),tf.ones([1])

(<tf.Tensor: id=96, shape=(1,), dtype=float32, numpy=array([0.],dtype=float32)>,
<tf.Tensor: id=99, shape=(1,), dtype=float32, numpy=array([1.],dtype=float32)>)

创建全 0 的矩阵：

tf.zeros([2,2])

<tf.Tensor: id=104, shape=(2, 2), dtype=float32, numpy=array([[0., 0.],[0., 0.]],dtype=float32)>

创建全 1 的矩阵：

tf.ones([3,2])

<tf.Tensor: id=108, shape=(3, 2), dtype=float32, numpy=array([[1., 1.],[1., 1.],[1., 1.]], dtype=float32)>

通过 tf.zeros_like, tf.ones_like 可以方便地新建与某个张量 shape 一致，内容全 0 或全 1
的张量。例如，创建与张量 a 形状一样的全 0 张量：

a = tf.ones([2,3])
tf.zeros_like(a)

<tf.Tensor: id=113, shape=(2, 3), dtype=float32, numpy=array([[0., 0., 0.],[0., 0., 0.]], dtype=float32)>

创建与张量 a 形状一样的全 1 张量：

a = tf.zeros([3,2])
tf.ones_like(a)

<tf.Tensor: id=120, shape=(3, 2), dtype=float32, numpy=array([[1., 1.],[1., 1.],[1., 1.]], dtype=float32)>

tf.*_like 是一个便捷函数，可以通过 tf.zeros(a.shape)等方式实现。

4.4.3 创建自定义数值张量

除了初始化为全 0，或全 1 的张量之外，有时也需要全部初始化为某个自定义数值的张量，比如将张量的数值全部初始化为-1 等。

通过tf.fill(shape, value)可以创建全为自定义数值 value 的张量。例如，创建元素为-1
的标量：

tf.fill([], -1)

<tf.Tensor: id=124, shape=(), dtype=int32, numpy=-1>

创建所有元素为-1 的向量：

tf.fill([1], -1)

<tf.Tensor: id=128, shape=(1,), dtype=int32, numpy=array([-1])>

创建所有元素为 99 的矩阵：

tf.fill([2,2], 99)

<tf.Tensor: id=136, shape=(2, 2), dtype=int32, numpy=array([[99, 99],[99, 99]])>

4.4.4 创建已知分布的张量

正态分布(Normal Distribution，或 Gaussian Distribution)和均匀分布(UniformDistribution)是最常见的分布之一，创建采样自这 2 种分布的张量非常有用，比如在卷积神经网络中，卷积核张量 W 初始化为正态分布有利于网络的训练；在对抗生成网络中，隐藏变量 z 一般采样自均匀分布。

通过 tf.random.normal(shape, mean=0.0, stddev=1.0)可以创建形状为 shape，均值为mean，标准差为 stddev 的正态分布(, 2)。例如，创建均值为 0，标准差为 1的正太分布：

tf.random.normal([2,2])

<tf.Tensor: id=143, shape=(2, 2), dtype=float32, numpy=array([[-0.4307344 , 0.44147003],[-0.6563149 , -0.30100572]], dtype=float32)>

创建均值为 1，标准差为 2 的正太分布：

tf.random.normal([2,2], mean=1,stddev=2)

<tf.Tensor: id=150, shape=(2, 2), dtype=float32, numpy=array([[-2.2687864, -0.7248812],[ 1.2752185, 2.8625617]], dtype=float32)>

通过 tf.random.uniform(shape, minval=0, maxval=None, dtype=tf.float32)可以创建采样自
[, ]区间的均匀分布的张量。例如创建采样自区间[0,1]，shape 为[2,2]的矩
阵：

tf.random.uniform([2,2])

<tf.Tensor: id=158, shape=(2, 2), dtype=float32, numpy=array([[0.65483284, 0.63064325],[0.008816 , 0.81437767]], dtype=float32)>

创建采样自区间[0,10]，shape 为[2,2]的矩阵：

tf.random.uniform([2,2],maxval=10)

<tf.Tensor: id=166, shape=(2, 2), dtype=float32, numpy=array([[4.541913 , 0.26521802],[2.578913 , 5.126876 ]], dtype=float32)>

如果需要均匀采样整形类型的数据，必须指定采样区间的最大值 maxval 参数，同时制定数据类型为 tf.int*型：

tf.random.uniform([2,2],maxval=100,dtype=tf.int32)

<tf.Tensor: id=171, shape=(2, 2), dtype=int32, numpy=array([[61, 21],[95, 75]])>

4.4.5 创建序列

在循环计算或者对张量进行索引时，经常需要创建一段连续的整形序列，可以通过tf.range()函数实现。tf.range(limit, delta=1)可以创建[0,)之间，步长为 delta 的整形序列，不包含 limit 本身。例如，创建 0~9，步长为 1 的整形序列：

tf.range(10)

<tf.Tensor: id=180, shape=(10,), dtype=int32, numpy=array([0, 1, 2, 3, 4, 5,6, 7, 8, 9])>

创建 0~9，步长为 2 的整形序列：

tf.range(10,delta=2)

<tf.Tensor: id=185, shape=(5,), dtype=int32, numpy=array([0, 2, 4, 6, 8])>

通过 tf.range(start, limit, delta=1)可以创建[, )，步长为 delta 的序列，不包含 limit
本身：

tf.range(1,10,delta=2)

<tf.Tensor: id=190, shape=(5,), dtype=int32, numpy=array([1, 3, 5, 7, 9])>

4.5 张量的典型应用

在介绍完张量的相关属性和创建方式后，我们将介绍每种维度下张量的典型应用，让读者在看到每种张量时，能够直观地联想到它主要的物理意义和用途，对后续张量的维度变换等一系列抽象操作的学习打下基础。本节在介绍典型应用时不可避免地会提及后续将要学习的网络模型或算法，学习时不需要完全理解，有初步印象即可。

4.5.1 标量

在 TensorFlow 中，标量最容易理解，它就是一个简单的数字，维度数为 0，shape 为[]。标量的典型用途之一是误差值的表示、各种测量指标的表示，比如准确度(Accuracy,acc)，精度(Precision)和召回率(Recall)等。

考虑某个模型的训练曲线，如图 4.1 所示，横坐标为训练 Batch 步数 Step，纵坐标分别为误差变化趋势(图 4.1(a))和准确度变化趋势曲线(图 4.1(b))，其中损失值 loss 和准确度均由张量计算产生，类型为标量。

以均方差误函数为例，经过 tf.keras.losses.mse(或 tf.keras.losses.MSE)返回每个样本上的误差值，最后取误差的均值作为当前 batch 的误差，它是一个标量：

out = tf.random.uniform([4,10]) #随机模拟网络输出
y = tf.constant([2,3,2,0]) # 随机构造样本真实标签
y = tf.one_hot(y, depth=10) # one-hot 编码
loss = tf.keras.losses.mse(y, out) # 计算每个样本的 MSE
loss = tf.reduce_mean(loss) # 平均 MSE
print(loss)

tf.Tensor(0.19950335, shape=(), dtype=float32)

4.5.2 向量

向量是一种非常常见的数据载体，如在全连接层和卷积神经网络层中，偏置张量就使用向量来表示。如图 4.2 所示，每个全连接层的输出节点都添加了一个偏置值，把所有输出节点的偏置表示成向量形式： = [1, 2]

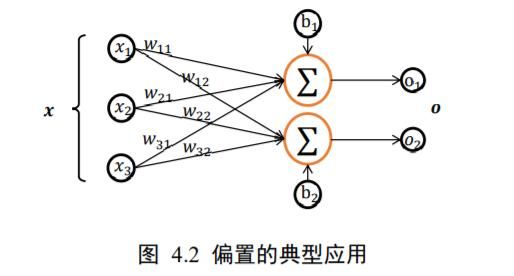
考虑 2 个输出节点的网络层，我们创建长度为 2 的偏置向量，并累加在每个输出节点上：
In [42]:

# z=wx,模拟获得激活函数的输入 z
z = tf.random.normal([4,2])
b = tf.zeros([2]) # 模拟偏置向量
z = z + b # 累加偏置

<tf.Tensor: id=245, shape=(4, 2), dtype=float32, numpy=
array([[ 0.6941646 , 0.4764454 ],
 [-0.34862405, -0.26460952],
 [ 1.5081744 , -0.6493869 ],
 [-0.26224667, -0.78742725]], dtype=float32)>

注意到这里 shape 为[4,2]的和 shape 为[2]的张量可以直接相加，这是为什么呢？让我们在 Broadcasting 一节为大家揭秘。

通过高层接口类 Dense()方式创建的网络层，张量 W 和存储在类的内部，由类自动创建并管理。可以通过全连接层的 bias 成员变量查看偏置变量，例如创建输入节点数为 4，输出节点数为 3 的线性层网络，那么它的偏置向量 b 的长度应为 3：

fc = layers.Dense(3) # 创建一层 Wx+b，输出节点为 3
# 通过 build 函数创建 W,b 张量，输入节点为 4
fc.build(input_shape=(2,4))
fc.bias # 查看偏置

<tf.Variable 'bias:0' shape=(3,) dtype=float32, numpy=array([0., 0., 0.],
dtype=float32)>

可以看到，类的偏置成员 bias 初始化为全 0，这也是偏置的默认初始化方案。

4.5.3 矩阵

矩阵也是非常常见的张量类型，比如全连接层的批量输入 = [, $d_{in}$ ]，其中表示输入样本的个数，即 batch size， $d_{in}$ 表示输入特征的长度。比如特征长度为 4，一共包含 2 个样本的输入可以表示为矩阵：

x = tf.random.normal([2,4])

令全连接层的输出节点数为 3，则它的权值张量 W 的 shape 为[4,3]:

w=tf.ones([4,3])
b=tf.zeros([3])
o =tf.matmul(x, w)+b
print(o)

<tf.Tensor: id=291, shape=(2, 3), dtype=float32, numpy=
array([[ 2.3506963, 2.3506963, 2.3506963],
 [-1.1724043, -1.1724043, -1.1724043]], dtype=float32)>

其中 X，W 张量均是矩阵。x*w+b 网络层称为线性层，在 TensorFlow 中可以通过 Dense类直接实现，Dense 层也称为全连接层。我们通过 Dense 类创建输入 4 个节点，输出 3 个节点的网络层，可以通过全连接层的 kernel 成员名查看其权值矩阵 W：

fc = layers.Dense(3) # 定义全连接层的输出节点为 3
fc.build(input_shape=(2,4)) # 定义全连接层的输入节点为 4
fc.kernel

<tf.Variable 'kernel:0' shape=(4, 3) dtype=float32, numpy=
array([[ 0.06468129, -0.5146048 , -0.12036425],
 [ 0.71618867, -0.01442951, -0.5891943 ],
 [-0.03011459, 0.578704 , 0.7245046 ],
 [ 0.73894167, -0.21171576, 0.4820758 ]], dtype=float32)>

4.5.4 三维张量

三维的张量一个典型应用是表示序列信号，它的格式是
= [, , ]

其中表示序列信号的数量，sequence len 表示序列信号在时间维度上的采样点数，featurelen 表示每个点的特征长度。

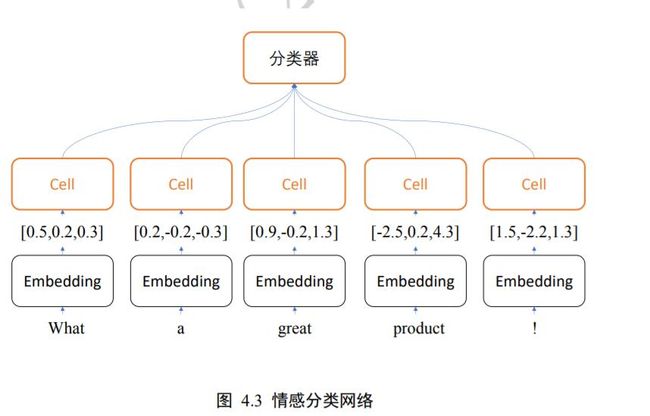
考虑自然语言处理中句子的表示，如评价句子的是否为正面情绪的情感分类任务网络，如图 4.3 所示。为了能够方便字符串被神经网络处理，一般将单词通过嵌入层(Embedding Layer)编码为固定长度的向量，比如“a”编码为某个长度 3 的向量，那么 2 个等长(单词数为 5)的句子序列可以表示为 shape 为[2,5,3]的 3 维张量，其中 2 表示句子个数，5 表示单词数量，3 表示单词向量的长度：

# 自动加载 IMDB 电影评价数据集
(x_train,y_train),(x_test,y_test)=keras.datasets.imdb.load_data(num_words=10000)
# 将句子填充、截断为等长 80 个单词的句子
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=80)
x_train.shape

可以看到 x_train 张量的 shape 为[25000,80]，其中 25000 表示句子个数，80 表示每个句子共 80 个单词，每个单词使用数字编码方式。我们通过 layers.Embedding 层将数字编码的单词转换为长度为 100 个词向量：

# 创建词向量 Embedding 层类
embedding=layers.Embedding(10000, 100)
# 将数字编码的单词转换为词向量
out = embedding(x_train)
out.shape

TensorShape([25000, 80, 100])

可以看到，经过 Embedding 层编码后，句子张量的 shape 变为[25000,80,100]，其中 100 表示每个单词编码为长度 100 的向量。

对于特征长度为 1 的序列信号，比如商品价格在 60 天内的变化曲线，只需要一个标量即可表示商品的价格，因此 2 件商品的价格变化趋势可以使用 shape 为[2,60]的张量表示。为了方便统一格式，也将价格变化趋势表达为 shape 为 [2,60,1]的张量，其中的 1 表示特征长度为 1。

4.5.5 4维张量

我们这里只讨论 3/4 维张量，大于 4 维的张量一般应用的比较少，如在元学习(metalearning)中会采用 5 维的张量表示方法，理解方法与 3/4 维张量类似。

4维张量在卷积神经网络中应用的非常广泛，它用于保存特征图(Feature maps)数据，格式一般定义为
$[b, h, w, c]$

其中表示输入的数量，h/w分布表示特征图的高宽，表示特征图的通道数，部分深度学习框架也会使用[, , ℎ, ]格式的特征图张量，例如 PyTorch。图片数据是特征图的一种，对于含有 RGB 3 个通道的彩色图片，每张图片包含了 h 行 w 列像素点，每个点需要 3 个数值表示 RGB 通道的颜色强度，因此一张图片可以表示为[h,w, 3]。如图 4.4 所示，最上层的图片表示原图，它包含了下面 3 个通道的强度信息。

神经网络中一般并行计算多个输入以提高计算效率，故张图片的张量可表示为[, ℎ, w, 3]。

# 创建 32x32 的彩色图片输入，个数为 4
x = tf.random.normal([4,32,32,3])
# 创建卷积神经网络
layer = layers.Conv2D(16,kernel_size=3)
out = layer(x) # 前向计算
out.shape # 输出大小

TensorShape([4, 30, 30, 16])

其中卷积核张量也是 4 维张量，可以通过 kernel 成员变量访问：

layer.kernel.shape
Out[49]: TensorShape([3, 3, 3, 16])

4.6 索引与切片

通过索引与切片操作可以提取张量的部分数据，使用频率非常高

4.6.1 索引

在 TensorFlow 中，支持基本的[][]…标准索引方式，也支持通过逗号分隔索引号的索引方式。考虑输入 X 为 4 张 32x32 大小的彩色图片(为了方便演示，大部分张量都使用随机分布模拟产生，后文同)，shape 为[4,32,32,3]，首先创建张量：

x = tf.random.normal([4,32,32,3])

接下来我们使用索引方式读取张量的部分数据。

❑ 取第 1 张图片的数据：

x[0]

<tf.Tensor: id=379, shape=(32, 32, 3), dtype=float32, numpy=
array([[[ 1.3005302 , 1.5301839 , -0.32005513],
 [-1.3020388 , 1.7837263 , -1.0747638 ], ...
 [-1.1092019 , -1.045254 , -0.4980363 ],
 [-0.9099222 , 0.3947732 , -0.10433522]]], dtype=float32)>

❑ 取第 1 张图片的第 2 行：

x[0][1]

<tf.Tensor: id=388, shape=(32, 3), dtype=float32, numpy=
array([[ 4.2904025e-01, 1.0574218e+00, 3.1540772e-01],
 [ 1.5800388e+00, -8.1637271e-02, 6.3147342e-01], ...,
 [ 2.8893018e-01, 5.8003378e-01, -1.1444757e+00],
 [ 9.6100050e-01, -1.0985689e+00, 1.0827581e+00]], dtype=float32)>

❑ 取第 1 张图片，第 2 行，第 3 列的像素：

In [53]: x[0][1][2]
Out[53]:
<tf.Tensor: id=401, shape=(3,), dtype=float32, numpy=array([-0.55954427,
0.14497331, 0.46424514], dtype=float32)>

❑ 取第 3 张图片，第 2 行，第 1 列的像素，B 通道(第 2 个通道)颜色强度值：

x[2][1][0][1]
Out[54]:
<tf.Tensor: id=418, shape=(), dtype=float32, numpy=-0.84922135>

当张量的维度数较高时，使用[][]. . .[]的方式书写不方便，可以采用[,, … , ]的方式索引，它们是等价的。

❑ 取第 2 张图片，第 10 行，第 3 列：

x[1,9,2]

<tf.Tensor: id=436, shape=(3,), dtype=float32, numpy=array([ 1.7487534 , -
0.41491988, -0.2944692 ], dtype=float32)>

4.6.2 切片

通过: : 切片方式可以方便地提取一段数据，其中 start 为开始读取位置的索引，end 为结束读取位置的索引(不包含 end 位)，step 为读取步长。

以 shape 为[4,32,32,3]的图片张量为例：

❑ 读取第 2和第3 张图片：

x[1:3]

<tf.Tensor: id=441, shape=(2, 32, 32, 3), dtype=float32, numpy=
array([[[[ 0.6920027 , 0.18658352, 0.0568333 ],
 [ 0.31422952, 0.75933754, 0.26853144],
 [ 2.7898 , -0.4284912 , -0.26247284],...

start: end: step切片方式有很多简写方式，其中 start、end、step 3 个参数可以根据需要选择性地省略，全部省略时即::，表示从最开始读取到最末尾，步长为 1，即不跳过任何元素。如 x[0,::]表示读取第 1 张图片的所有行，其中::表示在行维度上读取所有行，它等于x[0]的写法：

x[0,::]

<tf.Tensor: id=446, shape=(32, 32, 3), dtype=float32, numpy=
array([[[ 1.3005302 , 1.5301839 , -0.32005513],
 [-1.3020388 , 1.7837263 , -1.0747638 ],
 [-1.1230233 , -0.35004002, 0.01514002],

为了更加简洁，::可以简写为单个冒号:，如

x[:,0:28:2,0:28:2,:]

<tf.Tensor: id=451, shape=(4, 14, 14, 3), dtype=float32, numpy=
array([[[[ 1.3005302 , 1.5301839 , -0.32005513],
 [-1.1230233 , -0.35004002, 0.01514002],
 [ 1.3474811 , 0.639334 , -1.0826371 ],

表示取所有图片，隔行采样，隔列采样，所有通道信息，相当于在图片的高宽各缩放至原来的 50%。

我们来总结start: end: step切片的简写方式，其中从第一个元素读取时 start 可以省略，即 start=0 是可以省略，取到最后一个元素时 end 可以省略，步长为 1 时 step 可以省略，简写方式总结如表格 4.1：

特别地，step 可以为负数，考虑最特殊的一种例子，step = −1时，start: end: −1表示从 start 开始，逆序读取至 end 结束(不包含 end)，索引号 ≤ 。考虑一 0~9 简单序列，逆序取到第 1 号元素，不包含第 1 号：

x = tf.range(9)
x[8:0:-1]

<tf.Tensor: id=466, shape=(8,), dtype=int32, numpy=array([8, 7, 6, 5, 4, 3,2, 1])>

逆序取全部元素：

x[::-1]

<tf.Tensor: id=471, shape=(9,), dtype=int32, numpy=array([8, 7, 6, 5, 4, 3,2, 1, 0])>

逆序间隔采样：

x[::-2]

<tf.Tensor: id=476, shape=(5,), dtype=int32, numpy=array([8, 6, 4, 2, 0])>

读取每张图片的所有通道，其中行按着逆序隔行采样，列按着逆序隔行采样：

x = tf.random.normal([4,32,32,3])
x[0,::-2,::-2]

<tf.Tensor: id=487, shape=(16, 16, 3), dtype=float32, numpy=
array([[[ 0.63320625, 0.0655185 , 0.19056146],
 [-1.0078577 , -0.61400175, 0.61183935],
 [ 0.9230892 , -0.6860094 , -0.01580668],
 …

当张量的维度数量较多时，不需要采样的维度一般用单冒号:表示采样所有元素，此时有可能出现大量的:出现。继续考虑[4,32,32,3]的图片张量，当需要读取 G 通道上的数据时，前面所有维度全部提取，此时需要写为：

x[:,:,:,1]

<tf.Tensor: id=492, shape=(4, 32, 32), dtype=float32, numpy=
array([[[ 0.575703 , 0.11028383, -0.9950867 , ..., 0.38083118,
 -0.11705163, -0.13746642],
 ...

为了避免出现像[: , : , : ,1]这样出现过多冒号的情况，可以使用⋯符号表示取多个维度上所有的数据，其中维度的数量需根据规则自动推断：当切片方式出现⋯符号时，⋯符号左边的维度将自动对齐到最左边，⋯符号右边的维度将自动对齐到最右边，此时系统再自动推断⋯符号代表的维度数量，它的切片方式总结如表格 4.2：

考虑如下例子：

❑ 读取第 1-2 张图片的 G/B 通道数据：

In [64]: x[0:2,...,1:]
Out[64]:
<tf.Tensor: id=497, shape=(2, 32, 32, 2), dtype=float32, numpy=
array([[[[ 0.575703 , 0.8872789 ],
 [ 0.11028383, -0.27128693],
 [-0.9950867 , -1.7737272 ],
 ...

❑ 读取最后 2 张图片：

x[2:,...]

<tf.Tensor: id=502, shape=(2, 32, 32, 3), dtype=float32, numpy=
array([[[[-8.10753584e-01, 1.10984087e+00, 2.71821529e-01],
 [-6.10031188e-01, -6.47952318e-01, -4.07003373e-01],
 [ 4.62206364e-01, -1.03655539e-01, -1.18086267e+00],
 ...

❑ 读取 R/G 通道数据：

x[...,:2]

<tf.Tensor: id=507, shape=(4, 32, 32, 2), dtype=float32, numpy=
array([[[[-1.26881 , 0.575703 ],
 [ 0.98697686, 0.11028383],
 [-0.66420585, -0.9950867 ],
 ...

4.6.3 小结

张量的索引与切片方式多种多样，尤其是切片操作，初学者容易犯迷糊。但其实本质上切片操作只有: : 这一种基本形式，通过这种基本形式有目的地省略掉默认参数，从而衍生出多种简写方法，这也是很好理解的。它衍生的简写形式熟练后一看就能推测出省略掉的信息，书写起来也更方便快捷。由于深度学习一般处理的维度数在 4 维以内，⋯操作符完全可以用:符号代替，因此理解了这些就会发现张量切片操作并不复杂.

4.7 维度变换

在神经网络运算过程中，维度变换是最核心的张量操作，通过维度变换可以将数据任意地切换形式，满足不同场合的运算需求。

那么为什么需要维度变换呢？考虑线性层的批量形式：
$Y = X @ W + b$
其中 X 包含了 2 个样本，每个样本的特征长度为 4，X 的 shape 为[2,4]。线性层的输出为 3个节点，即 W 的 shape 定义为[4,3]，偏置的 shape 定义为[3]。那么X@W的运算张量shape 为[2,3]，需要叠加上 shape 为[3]的偏置。不同 shape 的 2 个张量怎么直接相加呢？

回到我们设计偏置的初衷，我们给每个层的每个输出节点添加一个偏置，这个偏置数据是对所有的样本都是共享的，换言之，每个样本都应该累加上同样的偏置向量，如图4.5 所示：

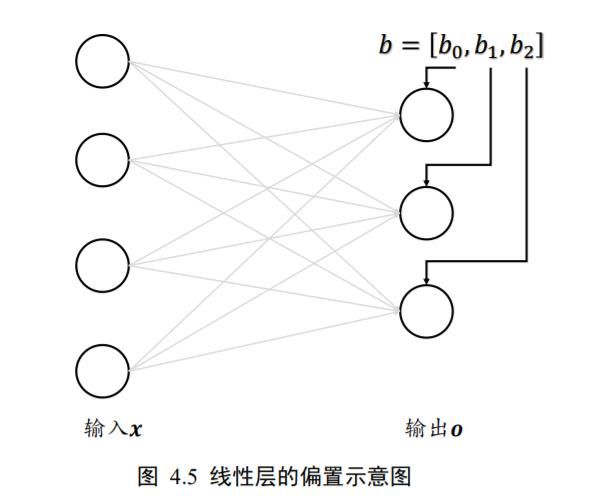
因此，对于 2 个样本的输入 X，我们需要将 shape 为[3]的偏置
$\boldsymbol{b}=\left[\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \end{array}\right]$
按样本数量复制 1 份，变成矩阵形式
$B^{\prime}=\left[\begin{array}{lll} b_{0} & b_{1} & b_{2} \\ b_{0} & b_{1} & b_{2} \end{array}\right]$
通过与X′ = X@W
$\mathrm{X}^{\prime}=\left[\begin{array}{lll} x_{00}^{\prime} & x_{01}^{\prime} & x_{02}^{\prime} \\ x_{10}^{\prime} & x_{11}^{\prime} & x_{12}^{\prime} \end{array}\right]$
相加，此时X′与 shape 相同，满足矩阵相加的数学条件：
$\mathrm{Y}=\mathrm{X}^{\prime}+\mathrm{B}^{\prime}=\left[\begin{array}{lll} x_{00}^{\prime} & x_{01}^{\prime} & x_{02}^{\prime} \\ x_{10}^{\prime} & x_{11}^{\prime} & x_{12}^{\prime} \end{array}\right]+\left[\begin{array}{lll} b_{0} & b_{1} & b_{2} \\ b_{0} & b_{1} & b_{2} \end{array}\right]$
通过这种方式，既满足了数学上矩阵相加需要 shape 一致的条件，又达到了给每个输入样本的输出节共享偏置的逻辑。为了实现这种运算方式，我们将插入一个新的维度，并把它定义为 batch 维度，然后在 batch 维度将数据复制 1 份，得到变换后的B′，新的 shape 为[2,3]。

算法的每个模块对于数据张量的格式有不同的逻辑要求，当现有的数据格式不满足算法要求时，需要通过维度变换将数据调整为正确的格式。这就是维度变换的功能。

基本的维度变换包含了改变视图 reshape，插入新维度 expand_dims，删除维度squeeze，交换维度 transpose，复制数据 tile 等

4.7.1 Reshape

在介绍改变视图操作之前，我们先来认识一下张量的存储和视图(View)的概念。张量的视图就是我们理解张量的方式，比如 shape 为[2,4,4,3]的张量 A，我们从逻辑上可以理解为 2 张图片，每张图片 4 行 4 列，每个位置有 RGB 3 个通道的数据；张量的存储体现在张量在内存上保存为一段连续的内存区域，对于同样的存储，我们可以有不同的理解方式，比如上述 A，我们可以在不改变张量的存储下，将张量 A 理解为 2 个样本，每个样本的特征为长度 48 的向量。这就是存储与视图的关系。

我们通过 tf.range()模拟生成 x 的数据：

x=tf.range(96)
x=tf.reshape(x,[2,4,4,3])

<tf.Tensor: id=11, shape=(2, 4, 4, 3), dtype=int32, numpy=
array([[[[ 0, 1, 2],
 [ 3, 4, 5],
 [ 6, 7, 8],
 [ 9, 10, 11]],…

在存储数据时，内存并不支持这个维度层级概念，只能以平铺方式按序写入内存，因此这种层级关系需要人为管理，也就是说，每个张量的存储顺序需要人为跟踪。为了方便表达，我们把张量 shape 中相对靠左侧的维度叫做大维度，shape 中相对靠右侧的维度叫做小维度，比如[2,4,4,3]的张量中，图片数量维度与通道数量相比，图片数量叫做大维度，通道数叫做小维度。在优先写入小维度的设定下，上述张量的内存布局为

数据在创建时按着初始的维度顺序写入，改变张量的视图仅仅是改变了张量的理解方式，并不会改变张量的存储顺序，这在一定程度上是从计算效率考虑的，大量数据的写入操作会消耗较多的计算资源。改变视图操作在提供便捷性的同时，也会带来很多逻辑隐患，这主要的原因是张量的视图与存储不同步造成的。我们先介绍合法的视图变换操作，再介绍不合法的视图变换。

比如张量按着初始视图[, ℎ, w, ]写入的内存布局，我们改变初始视图[, ℎ, w, ]的理解方式，它可以有多种合法理解方式：

❑ [, ℎ ∗w , ] 张量理解为 b 张图片，hw 个像素点，c 个通道
❑ [, ℎ, w∗ ] 张量理解为 b 张图片，h 行，每行的特征长度为 wc
❑ [, ℎ ∗ w∗ ] 张量理解为 b 张图片，每张图片的特征长度为 hwc

从语法上来说，视图变换只需要满足新视图的元素总量与内存区域大小相等即可，即新视图的元素数量等于
$b * h * w * c$

正是由于视图的设计约束很少，完全由用户定义，使得在改变视图时容易出现逻辑隐患。

现在我们来考虑不合法的视图变换。例如，如果定义新视图为[,w , ℎ, ]，[, , ℎ ∗w ]或者[, , ℎ, w]等时，与张量的存储顺序相悖，如果不同步更新张量的存储顺序，那么恢复出的数据将与新视图不一致，从而导致数据错乱。

为了能够正确恢复出数据，必须保证张量的存储顺序与新视图的维度顺序一致，例如根据图片数量-行-列-通道初始视图保存的张量，按照图片数量-行-列-通道( − ℎ −w − )的顺序可以获得合法数据。如果按着图片数量-像素-通道( b− h ∗ w − c)的方式恢复视图，也能得到合法的数据。但是如果按着图片数量-通道-像素( b− c − h ∗ w)的方式恢复数据，由于内存布局是按着图片数量-行-列-通道的顺序，视图维度与存储维度顺序相悖，提取的数据将是错乱的。

改变视图是神经网络中非常常见的操作，可以通过串联多个 Reshape 操作来实现复杂逻辑，但是在通过 Reshape 改变视图时，必须始终记住张量的存储顺序，新视图的维度顺序不能与存储顺序相悖，否则需要通过交换维度操作将存储顺序同步过来。

举个例子，对于 shape 为[4,32,32,3]的图片数据，通过 Reshape 操作将 shape 调整为[4,1024,3]，此时视图的维度顺序为 − − ，张量的存储顺序为[, ℎ, w, ]。可以将[4,1024,3]恢复为

❑ [, ℎ, w, ] = [4,32,32,3]时，新视图的维度顺序与存储顺序无冲突，可以恢复出无逻辑问题的数据
❑ [, w, ℎ, ] = [4,32,32,3]时，新视图的维度顺序与存储顺序冲突
❑ [ℎ ∗w ∗ , ] = [3072,4]时，新视图的维度顺序与存储顺序冲突

在 TensorFlow 中，可以通过张量的 ndim 和 shape 成员属性获得张量的维度数和形状：

x.ndim,x.shape
(4, TensorShape([2, 4, 4, 3]))

通过 tf.reshape(x, new_shape)，可以将张量的视图任意的合法改变：

tf.reshape(x,[2,-1])
<tf.Tensor: id=520, shape=(2, 48), dtype=int32, numpy=
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,…
 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]])>

其中的参数-1 表示当前轴上长度需要根据视图总元素不变的法则自动推导，从而方便用户书写。比如，上面的-1 可以推导为
$\frac{2 * 4 * 4 * 3}{2}=48$
再次改变数据的视图为[2,4,12]：

tf.reshape(x,[2,4,12])

<tf.Tensor: id=523, shape=(2, 4, 12), dtype=int32, numpy=
array([[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],…
 [36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]],
 [[48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59], …
 [84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]]])>

再次改变数据的视图为[2,16,3]：

tf.reshape(x,[2,-1,3])

<tf.Tensor: id=526, shape=(2, 16, 3), dtype=int32, numpy=
array([[[ 0, 1, 2], …
 [45, 46, 47]],
 [[48, 49, 50],…
 [93, 94, 95]]])>

通过上述的一系列连续变换视图操作时需要意识到，张量的存储顺序始终没有改变，数据在内存中仍然是按着初始写入的顺序0,1,2, … ,95保存的。

4.7.2 增删维度

增加维度 增加一个长度为 1 的维度相当于给原有的数据增加一个新维度的概念，维度长度为 1，故数据并不需要改变，仅仅是改变数据的理解方式，因此它其实可以理解为改变视图的一种特殊方式。

考虑一个具体例子，一张 28x28 灰度图片的数据保存为 shape 为[28,28]的张量，在末尾给张量增加一新维度，定义为为通道数维度，此时张量的 shape 变为[28,28,1]：

x = tf.random.uniform([28,28],maxval=10,dtype=tf.int32)

<tf.Tensor: id=552, shape=(28, 28), dtype=int32, numpy=
array([[4, 5, 7, 6, 3, 0, 3, 1, 1, 9, 7, 7, 3, 1, 2, 4, 1, 1, 9, 8, 6, 6,
 4, 9, 9, 4, 6, 0],…

通过 tf.expand_dims(x, axis)可在指定的 axis 轴前可以插入一个新的维度：

x = tf.expand_dims(x,axis=2)

<tf.Tensor: id=555, shape=(28, 28, 1), dtype=int32, numpy=
array([[[4],
 [5],
 [7],
 [6],
 [3],…

可以看到，插入一个新维度后，数据的存储顺序并没有改变，依然按着 4,5,7,6,3,0,…的顺序保存，仅仅是在插入一个新的维度后，改变了数据的视图。

同样的方法，我们可以在最前面插入一个新的维度，并命名为图片数量维度，长度为1，此时张量的 shape 变为[1,28,28,1]。

x = tf.expand_dims(x,axis=0)

<tf.Tensor: id=558, shape=(1, 28, 28), dtype=int32, numpy=
array([[[4, 5, 7, 6, 3, 0, 3, 1, 1, 9, 7, 7, 3, 1, 2, 4, 1, 1, 9, 8, 6,
 6, 4, 9, 9, 4, 6, 0],
 [5, 8, 6, 3, 6, 4, 3, 0, 5, 9, 0, 5, 4, 6, 4, 9, 4, 4, 3, 0, 6,
 9, 3, 7, 4, 2, 8, 9],…

需要注意的是，tf.expand_dims 的 axis 为正时，表示在当前维度之前插入一个新维度；为负时，表示当前维度之后插入一个新的维度。以[, ℎ, w, ]张量为例，不同 axis 参数的实际插入位置如下图 4.6 所示：

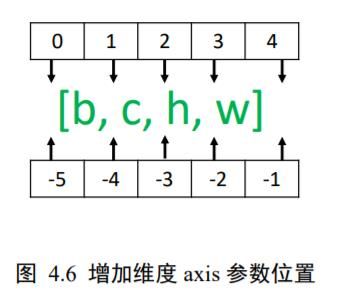
删除维度 是增加维度的逆操作，与增加维度一样，删除维度只能删除长度为 1 的维度，也不会改变张量的存储。继续考虑增加维度后 shape 为[1,28,28,1]的例子，如果希望将图片数量维度删除，可以通过 tf.squeeze(x, axis)函数，axis 参数为待删除的维度的索引号，图片数量的维度轴 axis=0：

x = tf.squeeze(x, axis=0)

<tf.Tensor: id=586, shape=(28, 28, 1), dtype=int32, numpy=
array([[[8],
 [2],
 [2],
 [0],…

继续删除通道数维度，由于已经删除了图片数量维度，此时的 x 的 shape 为[28,28,1]，因此删除通道数维度时指定 axis=2：

x = tf.squeeze(x, axis=2)

<tf.Tensor: id=588, shape=(28, 28), dtype=int32, numpy=
array([[8, 2, 2, 0, 7, 0, 1, 4, 9, 1, 7, 4, 8, 2, 7, 4, 8, 2, 9, 8, 8, 0,
 9, 9, 7, 5, 9, 7],
 [3, 4, 9, 9, 0, 6, 5, 7, 1, 9, 9, 1, 2, 7, 2, 7, 5, 3, 3, 7, 2, 4,
 5, 2, 7, 3, 8, 0],…

如果不指定维度参数 axis，即 ·tf.squeeze(x)·，那么他会默认删除所有长度为 1 的维度：

x = tf.random.uniform([1,28,28,1],maxval=10,dtype=tf.int32)
tf.squeeze(x)

<tf.Tensor: id=594, shape=(28, 28), dtype=int32, numpy=
array([[9, 1, 4, 6, 4, 9, 0, 0, 1, 4, 0, 8, 5, 2, 5, 0, 0, 8, 9, 4, 5, 0,
 1, 1, 4, 3, 9, 9],…

4.7.3 交换维度

改变视图、增删维度都不会影响张量的存储。在实现算法逻辑时，在保持维度顺序不变的条件下，仅仅改变张量的理解方式是不够的，有时需要直接调整的存储顺序，即交换维度(Transpose)。通过交换维度，改变了张量的存储顺序，同时也改变了张量的视图。

交换维度操作是非常常见的，比如在 TensorFlow 中，图片张量的默认存储格式是通道后行格式：[, ℎ, w, ]，但是部分库的图片格式是通道先行：[, , ℎ, w]，因此需要完成[, ℎ, w, ]到[, , ℎ,w ]维度交换运算。

我们以[, ℎ, w, ]转换到[, , ℎ,w ]为例，介绍如何使用 tf.transpose(x, perm)函数完成维度交换操作，其中 perm 表示新维度的顺序 List。考虑图片张量 shape 为[2,32,32,3]，图片数量、行、列、通道数的维度索引分别为 0,1,2,3，如果需要交换为[, , ℎ, w]格式，则新维度的排序为图片数量、通道数、行、列，对应的索引号为[0,3,1,2]，实现如下：

x = tf.random.normal([2,32,32,3])
tf.transpose(x,perm=[0,3,1,2])

<tf.Tensor: id=603, shape=(2, 3, 32, 32), dtype=float32, numpy=
array([[[[-1.93072677e+00, -4.80163872e-01, -8.85614634e-01, ...,
 1.49124235e-01, 1.16427064e+00, -1.47740364e+00],
 [-1.94761145e+00, 7.26879001e-01, -4.41877693e-01, ...

如果希望将[, ℎ, w, ]交换为[, w, ℎ, ]，即将行列维度互换，则新维度索引为[0,2,1,3]:

x = tf.random.normal([2,32,32,3])
tf.transpose(x,perm=[0,2,1,3])

<tf.Tensor: id=612, shape=(2, 32, 32, 3), dtype=float32, numpy=
array([[[[ 2.1266546 , -0.64206547, 0.01311932],
 [ 0.918484 , 0.9528751 , 1.1346699 ],
 ...,

需要注意的是，通过 tf.transpose 完成维度交换后，张量的存储顺序已经改变，视图也随之改变，后续的所有操作必须基于新的存续顺序进行。

4.7.4 数据复制

当通过增加维度操作插入新维度后，可能希望在新的维度上面复制若干份数据，满足后续算法的格式要求。

考虑 = @ + 的例子，偏置插入新维度后，需要在新维度上复制 batch size 份数据，将 shape 变为与@一致后，才能完成张量相加运算。可以通过tf.tile(x, multiples)函数完成数据在指定维度上的复制操作，multiples 分别指定了每个维度上面的复制倍数，对应位置为 1 表明不复制，为 2 表明新长度为原来的长度的 2 倍，即数据复制一份，以此类推。

以输入为[2,4]，输出为 3 个节点线性变换层为例，偏置定义为：
$\boldsymbol{b}=\left[\begin{array}{l} b_{0} \\ b_{1} \\ b_{2} \end{array}\right]$
通过 tf.expand_dims(b,axis=0)插入新维度：样本数量维度
$\left.\boldsymbol{b}=\left[\begin{array}{lll} b_{0} & b_{1} & b_{2} \end{array}\right]\right]$
此时的 shape 变为[1,3]，我们需要在 axis=0 图片数量维度上根据输入样本的数量复制若干次，这里的 batch size 为 2，变为矩阵 B：
$B=\left[\begin{array}{lll} b_{0} & b_{1} & b_{2} \\ b_{0} & b_{1} & b_{2} \end{array}\right]$
通过 tf.tile(b, multiples=[2,1])即可在 axis=0 维度复制 1 次，在 axis=1 维度不复制。首先插入新的维度：

b = tf.constant([1,2])
b = tf.expand_dims(b, axis=0)
b

<tf.Tensor: id=645, shape=(1, 2), dtype=int32, numpy=array([[1, 2]])>

在 batch 维度上复制数据 1 份：

b = tf.tile(b, multiples=[2,1])

<tf.Tensor: id=648, shape=(2, 2), dtype=int32, numpy=
array([[1, 2],
 [1, 2]])>

此时 B 的 shape 变为[2,3]，可以直接与X@W进行相加运算。

考虑另一个例子，输入 x 为 2 行 2 列的矩阵：

x = tf.range(4)
x=tf.reshape(x,[2,2])

<tf.Tensor: id=655, shape=(2, 2), dtype=int32, numpy=
array([[0, 1],
 [2, 3]])>

首先在列维度复制 1 份数据：

x = tf.tile(x,multiples=[1,2])

<tf.Tensor: id=658, shape=(2, 4), dtype=int32, numpy=
array([[0, 1, 0, 1],
 [2, 3, 2, 3]])>

然后在行维度复制 1 份数据：

x = tf.tile(x,multiples=[2,1])

<tf.Tensor: id=672, shape=(4, 4), dtype=int32, numpy=
array([[0, 1, 0, 1],
 [2, 3, 2, 3],
 [0, 1, 0, 1],
 [2, 3, 2, 3]])>

经过 2 个维度上的复制运算后，可以看到数据的变化过程，shape 也变为原来的 2 倍。

需要注意的是，tf.tile 会创建一个新的张量来保存复制后的张量，由于复制操作涉及到大量数据的读写 IO 运算，计算代价相对较高。神经网络中不同 shape 之间的运算操作十分频繁，那么有没有轻量级的复制操作呢？这就是接下来要介绍的 Broadcasting 操作。

4.8 Broadcasting

Broadcasting 也叫广播机制(自动扩展也许更合适)，它是一种轻量级张量复制的手段，在逻辑上扩展张量数据的形状，但是只要在需要时才会执行实际存储复制操作。对于大部分场景，Broadcasting 机制都能通过优化手段避免实际复制数据而完成逻辑运算，从而相对于 tf.tile 函数，减少了大量计算代价。

对于所有长度为 1 的维度，Broadcasting 的效果和 tf.tile 一样，都能在此维度上逻辑复制数据若干份，区别在于 tf.tile 会创建一个新的张量，执行复制 IO 操作，并保存复制后的张量数据，Broadcasting 并不会立即复制数据，它会逻辑上改变张量的形状，使得视图上变成了复制后的形状。

Broadcasting 会通过深度学习框架的优化手段避免实际复制数据而完成逻辑运算，至于怎么实现的用户不必关系，对于用户来说，Broadcasting 和 tf.tile 复制的最终效果是一样的，操作对用户透明，但是 Broadcasting 机制节省了大量计算资源，建议在运算过程中尽可能地利用 Broadcasting 提高计算效率。

继续考虑上述的Y = X@W + 的例子，X@W的 shape 为[2,3]，的 shape 为[3]，我们可以通过结合 tf.expand_dims 和 tf.tile 完成实际复制数据运算，将变换为[2,3]，然后与X@W完成相加。但实际上，我们直接将 shape 为[2,3]与[3]的相加：

x = tf.random.normal([2,4])
w = tf.random.normal([4,3])
b = tf.random.normal([3])
y = x@w+b

上述加法并没有发生逻辑错误，那么它是怎么实现的呢？这是因为它自动调用 Broadcasting函数 tf.broadcast_to(x, new_shape)，将 2 者 shape 扩张为相同的[2,3]，即上式可以等效为：

y = x@w + tf.broadcast_to(b,[2,3])

也就是说，操作符+在遇到 shape 不一致的 2 个张量时，会自动考虑将 2 个张量Broadcasting 到一致的 shape，然后再调用 tf.add 完成张量相加运算，这也就解释了我们之前一直存在的困惑。通过自动调用 tf.broadcast_to(b, [2,3])的 Broadcasting 机制，既实现了增加维度、复制数据的目的，又避免实际复制数据的昂贵计算代价，同时书写更加简洁高效。

那么有了Broadcasting 机制后，所有 shape 不一致的张量是不是都可以直接完成运算？很明显，所有的运算都需要在正确逻辑下进行，Broadcasting 机制并不会扰乱正常的计算逻辑，它只会针对于最常见的场景自动完成增加维度并复制数据的功能，提高开发效率和运行效率。这种最常见的场景是什么呢？这就要说到 Broadcasting 设计的核心思想。

Broadcasting 机制的核心思想是普适性，即同一份数据能普遍适合于其他位置。在验证普适性之前，需要将张量 shape 靠右对齐，然后进行普适性判断：对于长度为 1 的维度，默认这个数据普遍适合于当前维度的其他位置；对于不存在的维度，则在增加新维度后默认当前数据也是普适性于新维度的，从而可以扩展为更多维度数、其他长度的张量形状。

考虑 shape 为[ , 1]的张量 A，需要扩展为 shape：[, ℎ, w, ]，如图 4.7 所示，上行为欲扩展的 shape，下面为现有 shape：

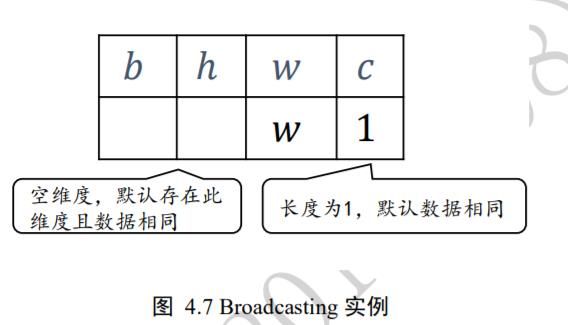
首先将 2 个 shape 靠右对齐，对于通道维度 c，张量的现长度为 1，则默认此数据同样适合当前维度的其他位置，将数据逻辑上复制 − 1份，长度变为 c；对于不存在的 b 和 h 维度，则自动插入新维度，新维度长度为 1，同时默认当前的数据普适于新维度的其他位置，即对于其它的图片、其他的行来说，与当前的这一行的数据完全一致。这样将数据b，h 维度的长度自动扩展为 b，h，如图 4.8 所示：

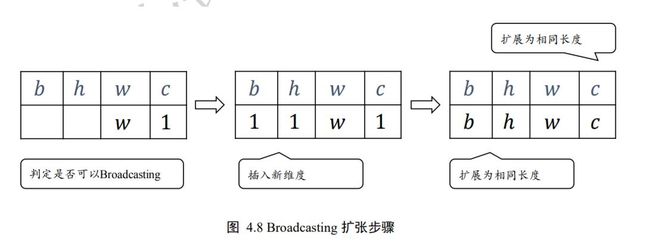
通过 tf.broadcast_to(x, new_shape)可以显式将现有 shape 扩张为 new_shape：

A = tf.random.normal([32,1])
tf.broadcast_to(A, [2,32,32,3])

<tf.Tensor: id=13, shape=(2, 32, 32, 3), dtype=float32, numpy=
array([[[[-1.7571245 , -1.7571245 , -1.7571245 ],
 [ 1.580159 , 1.580159 , 1.580159 ],
 [-1.5324328 , -1.5324328 , -1.5324328 ],...

可以看到，在普适性原则的指导下，Broadcasting 机制变得直观好理解，它的设计是非常符合人的思维模式。

我们来考虑不满足普适性原则的例子，如下图 4.9 所示：

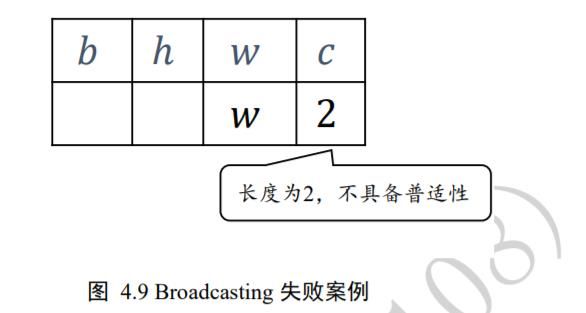
在 c 维度上，张量已经有 2 个特征数据，新 shape 对应维度长度为 c( ≠ 2，比如 c=3)，那么当前维度上的这 2 个特征无法普适到其他长度，故不满足普适性原则，无法应用Broadcasting 机制，将会触发错误：

A = tf.random.normal([32,2])
tf.broadcast_to(A, [2,32,32,4])

InvalidArgumentError: Incompatible shapes: [32,2] vs. [2,32,32,4]
[Op:BroadcastTo]

在进行张量运算时，有些运算可以在处理不同 shape 的张量时，会隐式自动调用Broadcasting 机制，如+，-，*，/等运算等，将参与运算的张量 Broadcasting 成一个公共shape，再进行相应的计算，如图 4.10 所示，演示了 3 种不同 shape 下的张量 A，B 相加的例子

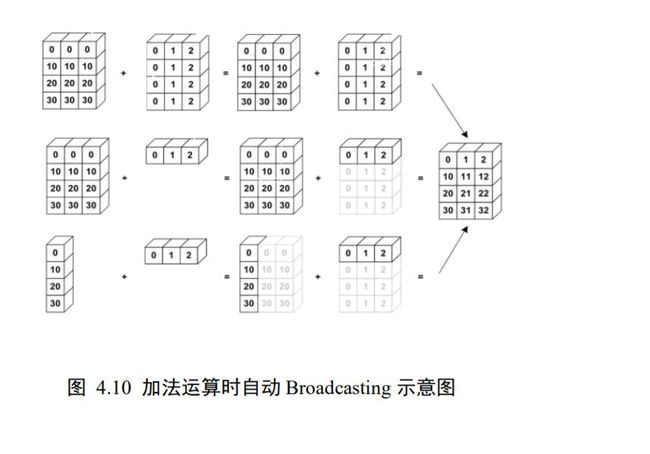
简单测试一下基本运算符的自动 Broadcasting 机制：

a = tf.random.normal([2,32,32,1])
b = tf.random.normal([32,32])
a+b,a-b,a*b,a/b

这些运算都能 Broadcasting 成[2,32,32,32]的公共 shape，再进行运算。熟练掌握并运用Broadcasting 机制可以让代码更简洁，计算效率更高。

4.9 数学运算

前面的章节我们已经使用了基本的加减乘除等数学运算函数，本节我们将系统地介绍TensorFlow 中常见的数学运算函数。

4.9.1 加减乘除

加减乘除是最基本的数学运算，分别通过 tf.add, tf.subtract, tf.multiply, tf.divide 函数实现，TensorFlow 已经重载了+ −∗/运算符，一般推荐直接使用运算符来完成加减乘除运算。

整除和余除也是常见的运算之一，分别通过//和%运算符实现。我们来演示整除运算：

a = tf.range(5)
b = tf.constant(2)
a//b
<tf.Tensor: id=115, shape=(5,), dtype=int32, numpy=array([0, 0, 1, 1, 2])>

余除运算：

a%b

<tf.Tensor: id=117, shape=(5,), dtype=int32, numpy=array([0, 1, 0, 1, 0])>

4.9.2 乘方

通过 tf.pow(x, a)可以方便地完成 = $x^{a}$ 乘方运算，也可以通过运算符**实现 ∗∗ 运算，实现如下：

x = tf.range(4)
tf.pow(x,3)

<tf.Tensor: id=124, shape=(4,), dtype=int32, numpy=array([ 0, 1, 8, 27])>

x**2

<tf.Tensor: id=127, shape=(4,), dtype=int32, numpy=array([0, 1, 4, 9])>

设置指数为 $\frac{1}{a}$ 形式即可实现根号运算： $\sqrt[a]{x}$ :

x=tf.constant([1.,4.,9.])
x**(0.5)

<tf.Tensor: id=139, shape=(3,), dtype=float32, numpy=array([1., 2., 3.],
dtype=float32)>

特别地，对于常见的平方和平方根运算，可以使用 tf.square(x)和 tf.sqrt(x)实现。平方运算实现如下：

x = tf.range(5)
x = tf.cast(x, dtype=tf.float32)
x = tf.square(x)

<tf.Tensor: id=159, shape=(5,), dtype=float32, numpy=array([ 0., 1., 4.,
9., 16.], dtype=float32)>

平方根运算实现如下：

tf.sqrt(x)

<tf.Tensor: id=161, shape=(5,), dtype=float32, numpy=array([0., 1., 2., 3.,
4.], dtype=float32)>

4.9.3 指数、对数

通过 tf.pow(a, x)或者**运算符可以方便实现指数运算 $a^{x}$ ：

x = tf.constant([1.,2.,3.])
2**x

<tf.Tensor: id=179, shape=(3,), dtype=float32, numpy=array([2., 4., 8.],
dtype=float32)>

特别地，对于自然指数 $e^{x}$ ,可以通过 tf.exp(x)实现：

tf.exp(1.)

<tf.Tensor: id=182, shape=(), dtype=float32, numpy=2.7182817>

在 TensorFlow 中，自然对数 $log _{e} x$ 可以通过 tf.math.log(x)实现:

x=tf.exp(3.)
tf.math.log(x)

<tf.Tensor: id=186, shape=(), dtype=float32, numpy=3.0>

如果希望计算其他底数的对数，可以根据对数的换底公式：
$\log _{a} x=\frac{\log _{e} x}{\log _{e} a}$
间接的通过 tf.math.log(x)实现。如计算 $log _{10} x$ 可以通过 $\frac{\log _{e} x}{\log _{e} 10}$ 实现如下：

x = tf.constant([1.,2.])
x = 10**x
tf.math.log(x)/tf.math.log(10.)

<tf.Tensor: id=222, shape=(2,), dtype=float32, numpy=array([0. ,
2.3025851], dtype=float32)>

实现起来相对繁琐，也许 TensorFlow 以后会推出任意底数的 log 函数.

4.9.4 矩阵相乘

神经网络中间包含了大量的矩阵相乘运算，前面我们已经介绍了通过@运算符可以方便的实现矩阵相乘，还可以通过 tf.matmul(a, b)实现。需要注意的是，TensorFlow 中的矩阵相乘可以使用批量方式，也就是张量 a,b 的维度数可以大于 2。当张量 a,b 维度数大于 2时，TensorFlow 会选择 a,b 的最后两个维度进行矩阵相乘，前面所有的维度都视作 Batch 维度。

根据矩阵相乘的定义，a 和 b 能够矩阵相乘的条件是，a 的倒数第一个维度长度(列)和b 的倒数第二个维度长度(行)必须相等。比如张量 a shape:[4,3,28,32]可以与张量 bshape:[4,3,32,2]进行矩阵相乘：

a = tf.random.normal([4,3,23,32])
b = tf.random.normal([4,3,32,2])
a@b

<tf.Tensor: id=236, shape=(4, 3, 28, 2), dtype=float32, numpy=
array([[[[-1.66706240e+00, -8.32602978e+00],
 [ 9.83304405e+00, 8.15909767e+00],
 [ 6.31014729e+00, 9.26124632e-01],…

得到 shape 为[4,3,28,2]的结果。

矩阵相乘函数支持自动 Broadcasting机制：

a = tf.random.normal([4,28,32])
b = tf.random.normal([32,16])
tf.matmul(a,b)

<tf.Tensor: id=264, shape=(4, 28, 16), dtype=float32, numpy=
array([[[-1.11323869e+00, -9.48194981e+00, 6.48123884e+00, ...,
 6.53280640e+00, -3.10894990e+00, 1.53050375e+00],
 [ 4.35898495e+00, -1.03704405e+01, 8.90656471e+00, ...,

4.10 前向传播实战

到现在为止，我们已经介绍了如何创建张量，对张量进行索引切片，维度变换和常见的数学运算等操作。本节我们将利用我们已经学到的知识去完成三层神经网络的实现：
$\left.\text {out}\left.=\text {relu\{relu\{relu}\left[X @ W_{1}+b_{1}\right] @ W_{2}+b_{2}\right\} @ W_{3}+b_{3}\right\}$

我们采用的数据集是 MNIST 手写数字图片集，输入节点数为 784，第一层的输出节点数是256，第二层的输出节点数是 128，第三层的输出节点是 10，也就是当前样本属于 10 类别的概率。

首先创建每个非线性函数的 w,b 参数张量：

w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev=0.1))
b3 = tf.Variable(tf.zeros([10]))

在前向计算时，首先将 shape 为[, 28,28]的输入数据 Reshape 为[, 784]:

 # [b, 28, 28] => [b, 28*28]
 x = tf.reshape(x, [-1, 28*28])

完成第一个非线性函数的计算，我们这里显示地进行 Broadcasting:

 # [b, 784]@[784, 256] + [256] => [b, 256] + [256] => [b, 256] +[b, 256]
 h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
 h1 = tf.nn.relu(h1)

同样的方法完成第二个和第三个非线性函数的前向计算，输出层可以不使用 ReLU 激活函数：

 # [b, 256] => [b, 128]
 h2 = h1@w2 + b2
 h2 = tf.nn.relu(h2)
 # [b, 128] => [b, 10]
 out = h2@w3 + b3

将真实的标注张量 y 转变为 one-hot 编码，并计算与 out 的均方差：

 # mse = mean(sum(y-out)^2)
 # [b, 10]
 loss = tf.square(y_onehot - out)
 # mean: scalar
 loss = tf.reduce_mean(loss)

上述的前向计算过程都需要包裹在 with tf.GradientTape() as tape 上下文中，使得前向计算时能够保存计算图信息，方便反向求导运算。
通过 tape.gradient()函数求得网络参数到梯度信息：

 # compute gradients
 grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])

并按照
$\theta^{\prime}=\theta-\eta * \frac{\partial \mathcal{L}}{\partial \theta}$
来更新网络参数：

# w1 = w1 - lr * w1_grad
 w1.assign_sub(lr * grads[0])
 b1.assign_sub(lr * grads[1])
 w2.assign_sub(lr * grads[2])
 b2.assign_sub(lr * grads[3])
 w3.assign_sub(lr * grads[4])
 b3.assign_sub(lr * grads[5])

其中 assign_sub()将原地(In-place)减去给定的参数值，实现参数的自我更新操作。网络训练
误差值的变化曲线如图 4.11 所示。

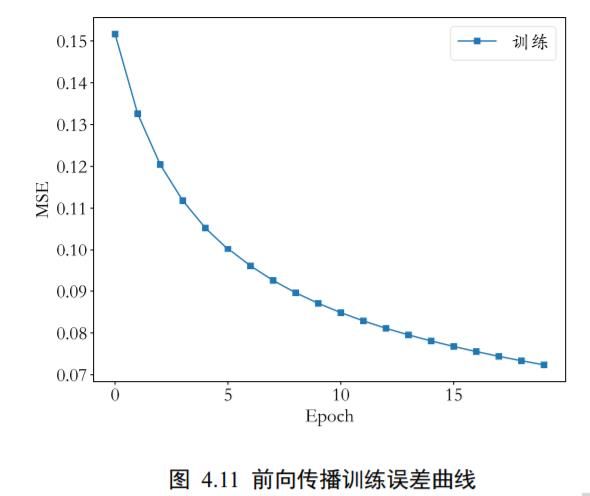
第5章 TensorFlow 进阶

在介绍完张量的基本操作后，我们来进一步学习张量的进阶操作，如张量的合并与分割，范数统计，张量填充，限幅等，并用过 MNIST 数据集的测试实战加深读者对TensorFlow 张量操作的立即。

5.1 合并与分割

5.1.1 合并

合并是指将多个张量在某个维度上合并为一个张量。以某学校班级成绩册数据为例，设张量 A 保存了某学校 1-4 号班级的成绩册，每个班级 35 个学生，共 8 门科目，则张量 A的 shape 为：[4,35,8]；同样的方式，张量 B 保存了剩下的 6 个班级的成绩册，shape 为[6,35,8]。通过合并 2 个成绩册，便可得到学校所有班级的成绩册张量 C，shape 应为[10,35,8]。这就是张量合并的意义所在。张量的合并可以使用拼接(Concatenate)和堆叠(Stack)操作实现，拼接并不会产生新的维度，而堆叠会创建新维度。选择使用拼接还是堆叠操作来合并张量，取决于具体的场景是否需要创建新维度。

拼接在 TensorFlow 中，可以通过 tf.concat(tensors, axis)，其中 tensors 保存了所有需要合并的张量 List，axis 指定需要合并的维度。回到上面的例子，这里班级维度索引号为 0，即 axis=0，合并张量 A,B 如下：

a = tf.random.normal([4,35,8]) # 模拟成绩册 A
b = tf.random.normal([6,35,8]) # 模拟成绩册 B
tf.concat([a,b],axis=0) # 合并成绩册

<tf.Tensor: id=13, shape=(10, 35, 8), dtype=float32, numpy=
array([[[ 1.95299834e-01, 6.87859178e-01, -5.80048323e-01, ...,
 1.29430830e+00, 2.56610274e-01, -1.27798581e+00],
 [ 4.29753691e-01, 9.11329567e-01, -4.47975427e-01, ...,

除了可以在班级维度上进行合并，还可以在其他维度上合并张量。考虑张量 A 保存了所有班级所有学生的前 4 门科目成绩，shape 为[10,35,4]，张量 B 保存了剩下的 4 门科目成绩，shape 为[10,35,4]，则可以合并 shape 为[10,35,8]的总成绩册张量：

a = tf.random.normal([10,35,4])
b = tf.random.normal([10,35,4])
tf.concat([a,b],axis=2) # 在科目维度拼接

<tf.Tensor: id=28, shape=(10, 35, 8), dtype=float32, numpy=
array([[[-5.13509691e-01, -1.79707789e+00, 6.50747120e-01, ...,
 2.58447856e-01, 8.47878829e-02, 4.13468748e-01],
 [-1.17108583e+00, 1.93961406e+00, 1.27830813e-02, ...,

合并操作可以在任意的维度上进行，唯一的约束是非合并维度的长度必须一致。比如 shape为[4,32,8]和 shape 为[6,35,8]的张量则不能直接在班级维度上进行合并，因为学生数维度的长度并不一致，一个为 32，另一个为 35：

a = tf.random.normal([4,32,8])
b = tf.random.normal([6,35,8])
tf.concat([a,b],axis=0) # 非法拼接

InvalidArgumentError: ConcatOp : Dimensions of inputs should match: shape[0]
= [4,32,8] vs. shape[1] = [6,35,8] [Op:ConcatV2] name: concat

堆叠 tf.concat 直接在现有维度上面合并数据，并不会创建新的维度。如果在合并数据时，希望创建一个新的维度，则需要使用 tf.stack 操作。考虑张量 A 保存了某个班级的成绩册，shape 为[35,8]，张量 B 保存了另一个班级的成绩册，shape 为[35,8]。合并这 2 个班级的数据时，需要创建一个新维度，定义为班级维度，新维度可以选择放置在任意位置，一般根据大小维度的经验法则，将较大概念的班级维度放置在学生维度之前，则合并后的张量的新 shape 应为[2,35,8]。

使用 tf.stack(tensors, axis)可以合并多个张量 tensors，其中 axis 指定插入新维度的位置，axis 的用法与 tf.expand_dims 的一致，当axis ≥ 0时，在 axis 之前插入;当axis < 0时，在 axis 之后插入新维度例如 shape 为[, , ℎ, ]的张量，在不同位置通过 stack 操作插入新维度，axis 参数对应的插入位置设置如图 5.1 所示：

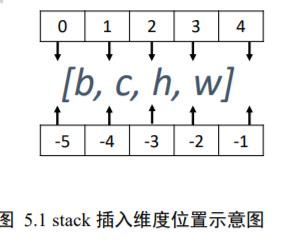
堆叠方式合并这 2 个班级成绩册如下：

a = tf.random.normal([35,8])
b = tf.random.normal([35,8])
tf.stack([a,b],axis=0) # 堆叠合并为 2 个班级

<tf.Tensor: id=55, shape=(2, 35, 8), dtype=float32, numpy=
array([[[ 3.68728966e-01, -8.54765773e-01, -4.77824420e-01,
 -3.83714020e-01, -1.73216307e+00, 2.03872994e-02,
 2.63810277e+00, -1.12998331e+00],…

同样可以选择在其他位置插入新维度，如在最末尾插入：

a = tf.random.normal([35,8])
b = tf.random.normal([35,8])
tf.stack([a,b],axis=-1) # 在末尾插入班级维度

<tf.Tensor: id=69, shape=(35, 8, 2), dtype=float32, numpy=
array([[[ 0.3456724 , -1.7037214 ],
 [ 0.41140947, -1.1554345 ],
 [ 1.8998919 , 0.56994915],…

此时班级的维度在 axis=2 轴上面，理解时也需要按着最新的维度顺序去理解数据。若选择使用 tf.concat 上述成绩单，则可以合并为：

a = tf.random.normal([35,8])
b = tf.random.normal([35,8])
tf.concat([a,b],axis=0) # 拼接方式合并，没有 2 个班级的概念

<tf.Tensor: id=108, shape=(70, 8), dtype=float32, numpy=
array([[-0.5516891 , -1.5031327 , -0.35369992, 0.31304857, 0.13965549,
 0.6696881 , -0.50115544, 0.15550546],
 [ 0.8622069 , 1.0188094 , 0.18977325, 0.6353301 , 0.05809061,…

tf.concat 也可以顺利合并数据，但是在理解时，需要按着前 35 个学生来自第一个班级，后35 个学生来自第二个班级的方式。在这里，明显通过 tf.stack 方式创建新维度的方式更合理，得到的 shape 为[2,35,8]的张量也更容易理解。

tf.stack 也需要满足张量堆叠合并条件，它需要所有合并的张量 shape 完全一致才可合并。我们来看张量 shape 不一致时进行堆叠合并会发生的错误：

a = tf.random.normal([35,4])
b = tf.random.normal([35,8])
tf.stack([a,b],axis=-1) # 非法堆叠操作

InvalidArgumentError: Shapes of all inputs must match: values[0].shape =
[35,4] != values[1].shape = [35,8] [Op:Pack] name: stack

上述操作尝试合并 shape 为[35,4]和[35,8]的 2 个张量，由于 2 者形状不一致，无法完成合并操作。

5.1.2 分割

合并操作的逆过程就是分割，将一个张量分拆为多个张量。继续考虑成绩册的例子，我们得到整个学校的成绩册张量，shape 为[10,35,8]，现在需要将数据在班级维度切割为10 个张量，每个张量保存了对应班级的成绩册。

通过 tf.split(x, axis, num_or_size_splits)可以完成张量的分割操作，其中

❑ x：待分割张量
❑ axis：分割的维度索引号
❑ num_or_size_splits：切割方案。当 num_or_size_splits 为单个数值时，如 10，表示切割为 10 份；当 num_or_size_splits 为 List 时，每个元素表示每份的长度，如[2,4,2,2]表示切割为 4 份，每份的长度分别为 2,4,2,2

现在我们将总成绩册张量切割为 10 份：

x = tf.random.normal([10,35,8])
# 等长切割
result = tf.split(x,axis=0,num_or_size_splits=10)
len(result)  #[1,35,8]

10

可以查看切割后的某个张量的形状，它应是某个班级的所有成绩册数据，shape 为[35,8]之类：

result[0]

Out[9]: <tf.Tensor: id=136, shape=(1, 35, 8), dtype=float32, numpy=
array([[[-1.7786729 , 0.2970506 , 0.02983334, 1.3970423 ,
 1.315918 , -0.79110134, -0.8501629 , -1.5549672 ],
 [ 0.5398711 , 0.21478991, -0.08685189, 0.7730989 ,…

可以看到，切割后的班级 shape 为[1,35,8]，保留了班级维度，这一点需要注意。我们进行不等长的切割：将数据切割为 4份，每份长度分别为[4,2,2,2]:

x = tf.random.normal([10,35,8])
# 自定义长度的切割
result = tf.split(x,axis=0,num_or_size_splits=[4,2,2,2])
len(result)

4

查看第一个张量的 shape，根据我们的切割方案，它应该包含了 4 个班级的成绩册：

result[0]

<tf.Tensor: id=155, shape=(4, 35, 8), dtype=float32, numpy=
array([[[-6.95693314e-01, 3.01393479e-01, 1.33964568e-01, ...,

特别地，如果希望在某个维度上全部按长度为 1 的方式分割，还可以直接使用 tf.unstack(x,axis)。这种方式是 tf.split 的一种特殊情况，切割长度固定为 1，只需要指定切割维度即可。例如，将总成绩册张量在班级维度进行 unstack：

x = tf.random.normal([10,35,8])
result = tf.unstack(x,axis=0) # Unstack 为长度为 1
len(result)

10

查看切割后的张量的形状：

result[0]

<tf.Tensor: id=166, shape=(35, 8), dtype=float32, numpy=
array([[-0.2034383 , 1.1851563 , 0.25327438, -0.10160723, 2.094969 ,
 -0.8571669 , -0.48985648, 0.55798006],…

可以看到，通过 tf.unstack 切割后，shape 变为[35,8]，即班级维度消失了，这也是与 tf.split
区别之处。

5.2 数据统计

在神经网络的计算过程中，经常需要统计数据的各种属性，如最大值，均值，范数等等。由于张量通常 shape 较大，直接观察数据很难获得有用信息，通过观察这些张量统计信息可以较轻松地推测张量数值的分布。

5.2.1 向量范数

向量范数(Vector norm)是表征向量“长度”的一种度量方法，在神经网络中，常用来表示张量的权值大小，梯度大小等。常用的向量范数有：

❑ L1 范数，定义为向量的所有元素绝对值之和
$\|x\|_{1}=\sum_{i}\left|x_{i}\right|$
❑ L2 范数，定义为向量的所有元素的平方和，再开根号
$\|x\|_{2}=\sqrt{\sum_{i}\left|x_{i}\right|^{2}}$
❑ ∞ −范数，定义为向量的所有元素绝对值的最大值：
$\|x\|_{\infty}=\max _{i}\left(\left|x_{i}\right|\right)$

对于矩阵、张量，同样可以利用向量范数的计算公式，等价于将矩阵、张量打平成向量后计算。

在 TensorFlow 中，可以通过 tf.norm(x, ord)求解张量的 L1, L2, ∞等范数，其中参数 ord指定为 1,2 时计算 L1, L2 范数，指定为 np.inf 时计算∞ −范数：

x = tf.ones([2,2])
tf.norm(x,ord=1) # 计算 L1 范数

<tf.Tensor: id=183, shape=(), dtype=float32, numpy=4.0>

tf.norm(x,ord=2) # 计算 L2 范数

Out[14]: <tf.Tensor: id=189, shape=(), dtype=float32, numpy=2.0>

import numpy as np
tf.norm(x,ord=np.inf) # 计算∞范数
Out[15]: <tf.Tensor: id=194, shape=(), dtype=float32, numpy=1.0>

5.2.2 最大最小值、均值、和

通过 tf.reduce_max, tf.reduce_min, tf.reduce_mean, tf.reduce_sum 可以求解张量在某个维度上的最大、最小、均值、和，也可以求全局最大、最小、均值、和信息。

考虑 shape 为[4,10]的张量，其中第一个维度代表样本数量，第二个维度代表了当前样本分别属于 10 个类别的概率，需要求出每个样本的概率最大值为：

x = tf.random.normal([4,10])
tf.reduce_max(x,axis=1) # 统计概率维度上的最大值

Out[16]:<tf.Tensor: id=203, shape=(4,), dtype=float32,
numpy=array([1.2410722 , 0.88495886, 1.4170984 , 0.9550192 ],
dtype=float32)>

同样求出每个样本概率的最小值：

tf.reduce_min(x,axis=1) # 统计概率维度上的最小值

Out[17]:<tf.Tensor: id=206, shape=(4,), dtype=float32, numpy=array([-
0.27862206, -2.4480672 , -1.9983795 , -1.5287997 ], dtype=float32)>

求出每个样本的概率的均值：

tf.reduce_mean(x,axis=1) # 统计概率维度上的均值

Out[18]:<tf.Tensor: id=209, shape=(4,), dtype=float32,
numpy=array([ 0.39526337, -0.17684573, -0.148988 , -0.43544054],
dtype=float32)>

当不指定 axis 参数时，tf.reduce_*函数会求解出全局元素的最大、最小、均值、和：

x = tf.random.normal([4,10])
# 统计全局的最大、最小、均值、和
tf.reduce_max(x),tf.reduce_min(x),tf.reduce_mean(x)

Out [19]: (<tf.Tensor: id=218, shape=(), dtype=float32, numpy=1.8653786>,
<tf.Tensor: id=220, shape=(), dtype=float32, numpy=-1.9751656>,
<tf.Tensor: id=222, shape=(), dtype=float32, numpy=0.014772797>)

在求解误差函数时，通过 TensorFlow 的 MSE 误差函数可以求得每个样本的误差，需要计算样本的平均误差，此时可以通过 tf.reduce_mean 在样本数维度上计算均值：

out = tf.random.normal([4,10]) # 网络预测输出
y = tf.constant([1,2,2,0]) # 真实标签
y = tf.one_hot(y,depth=10) # one-hot 编码
loss = keras.losses.mse(y,out) # 计算每个样本的误差
loss = tf.reduce_mean(loss) # 平均误差
loss

<tf.Tensor: id=241, shape=(), dtype=float32, numpy=1.1921183>

与均值函数相似的是求和函数 tf.reduce_sum(x,axis)，它可以求解张量在 axis 轴上所有特征的和：

out = tf.random.normal([4,10])
tf.reduce_sum(out,axis=-1) # 求和

Out[21]:<tf.Tensor: id=303, shape=(4,), dtype=float32, numpy=array([-
0.588144 , 2.2382064, 2.1582587, 4.962141 ], dtype=float32)>

除了希望获取张量的最值信息，还希望获得最值所在的索引号，例如分类任务的标签预测。

考虑 10 分类问题，我们得到神经网络的输出张量 out，shape 为[2,10]，代表了 2 个样本属于 10 个类别的概率，由于元素的位置索引代表了当前样本属于此类别的概率，预测时往往会选择概率值最大的元素所在的索引号作为样本类别的预测值：

out = tf.random.normal([2,10])
out = tf.nn.softmax(out, axis=1) # 通过 softmax 转换为概率值
out

Out[22]:<tf.Tensor: id=257, shape=(2, 10), dtype=float32, numpy=
array([
[0.18773547, 0.1510464 , 0.09431915, 0.13652141, 0.06579739,0.02033597, 0.06067333, 0.0666793 , 0.14594753, 0.07094406],
[0.5092072 , 0.03887136, 0.0390687 , 0.01911005, 0.03850609,0.03442522, 0.08060656, 0.10171875, 0.08244187, 0.05604421]],
 dtype=float32)>

以第一个样本为例，可以看到，它概率最大的索引为 = 0，最大概率值为 0.1877。由于每个索引号上的概率值代表了样本属于此索引号的类别的概率，因此第一个样本属于 0 类的概率最大，在预测时考虑第一个样本应该最有可能属于类别 0。这就是需要求解最大值的索引号的一个典型应用。通过 tf.argmax(x, axis)，tf.argmin(x, axis)可以求解在 axis 轴上，x 的最大值、最小值所在的索引号：

pred = tf.argmax(out, axis=1) # 选取概率最大的位置
pred

Out[23]:<tf.Tensor: id=262, shape=(2,), dtype=int64, numpy=array([0, 0],
dtype=int64)>

可以看到，这 2 个样本概率最大值都出现在索引 0 上，因此最有可能都是类别 0，我们将类别 0 作为这 2 个样本的预测类别。

5.3 张量比较

为了计算分类任务的准确率等指标，一般需要将预测结果和真实标签比较，统计比较结果中正确的数量来就是计算准确率。考虑 100 个样本的预测结果：

out = tf.random.normal([100,10])
out = tf.nn.softmax(out, axis=1) # 输出转换为概率
pred = tf.argmax(out, axis=1) # 选取预测值
Out[24]:<tf.Tensor: id=272, shape=(100,), dtype=int64, numpy=
array([0, 6, 4, 3, 6, 8, 6, 3, 7, 9, 5, 7, 3, 7, 1, 5, 6, 1, 2, 9, 0, 6,
 5, 4, 9, 5, 6, 4, 6, 0, 8, 4, 7, 3, 4, 7, 4, 1, 2, 4, 9, 4,…

可以看到我们模拟的 100 个样本的预测值，我们与这 100 样本的真实值比较：

# 真实标签
y = tf.random.uniform([100],dtype=tf.int64,maxval=10)

Out[25]:<tf.Tensor: id=281, shape=(100,), dtype=int64, numpy=
array([0, 9, 8, 4, 9, 7, 2, 7, 6, 7, 3, 4, 2, 6, 5, 0, 9, 4, 5, 8, 4, 2,
 5, 5, 5, 3, 8, 5, 2, 0, 3, 6, 0, 7, 1, 1, 7, 0, 6, 1, 2, 1, 3, …

即可获得每个样本是否预测正确。通过 tf.equal(a, b)(或 tf.math.equal(a, b))函数可以比较这 2个张量是否相等：

out = tf.equal(pred,y) # 预测值与真实值比较

Out[26]:<tf.Tensor: id=288, shape=(100,), dtype=bool, numpy=
array([False, False, False, False, True, False, False, False, False,
 False, False, False, False, False, True, False, False, True,…

tf.equal()函数返回布尔型的张量比较结果，只需要统计张量中 True 元素的个数，即可知道预测正确的个数。为了达到这个目的，我们先将布尔型转换为整形张量，再求和其中 1 的个数，可以得到比较结果中 True 元素的个数：

out = tf.cast(out, dtype=tf.float32) # 布尔型转 int 型
correct = tf.reduce_sum(out) # 统计 True 的个数

Out[27]:<tf.Tensor: id=293, shape=(), dtype=float32, numpy=12.0>

可以看到，我们随机产生的预测数据的准确度是
$\text { accuracy }=\frac{12}{100}=12 \%$
这也是随机预测模型的正常水平。

除了比较相等的 tf.equal(a, b)函数，其他的比较函数用法类似，如表格 5.1 所示：

5.4 填充与复制

5.4.1 填充

对于图片数据的高和宽、序列信号的长度，维度长度可能各不相同。为了方便网络的并行计算，需要将不同长度的数据扩张为相同长度，之前我们介绍了通过复制的方式可以增加数据的长度，但是重复复制数据会破坏原有的数据结构，并不适合于此处。通常的做法是，在需要补充长度的信号开始或结束处填充足够数量的特定数值，如 0，使得填充后的长度满足系统要求。那么这种操作就叫做填充(Padding)。

考虑 2 个句子张量，每个单词使用数字编码的方式，如 1 代表 I，2 代表 like 等。第一个句子为：

“I like the weather today.”

我们假设句子编码为：[1,2,3,4,5,6]，第二个句子为:

“So do I.”

它的编码为：[7,8,1,6]。为了能够保存在同一个张量中，我们需要将这两个句子的长度保持一致，也就是说，需要将第二个句子的长度扩充为 6。常见的填充方案是在句子末尾填充若干数量的 0，变成：

[7,8,1,6,0,0]

此时这两个句子堆叠合并 shape 为[2,6]的张量。

填充操作可以通过 tf.pad(x, paddings)函数实现，paddings 是包含了多个[ , ℎ ]的嵌套方案 List.

如[[0,0],[2,1],[1,2]]表示第一个维度不填充，第二个维度左边(起始处)填充两个单元，右边(结束处)填充一个单元，第三个维度左边填充一个单元，右边填充两个单元。

考虑上述 2 个句子的例子，需要在第二个句子的第一个维度的右边填充 2 个单元，则 paddings 方案为[[0,2]]：

a = tf.constant([1,2,3,4,5,6])
b = tf.constant([7,8,1,6])
b = tf.pad(b, [[0,2]]) # 填充
b

Out[28]:<tf.Tensor: id=3, shape=(6,), dtype=int32, numpy=array([7, 8, 1, 6,
0, 0])>

填充后句子张量形状一致，再将这 2 句子 Stack 在一起：

tf.stack([a,b],axis=0) # 合并

Out[29]:<tf.Tensor: id=5, shape=(2, 6), dtype=int32, numpy=
array([[1, 2, 3, 4, 5, 6],
 [7, 8, 1, 6, 0, 0]])>

在自然语言处理中，需要加载不同句子长度的数据集，有些句子长度较小，如 10 个单词左右，部份句子长度较长，如超过 100 个单词。为了能够保存在同一张量中，一般会选取能够覆盖大部分句子长度的阈值，如 80 个单词：对于小于 80 个单词的句子，在末尾填充相应数量的 0；对大于 80 个单词的句子，截断超过规定长度的部分单词。以 IMDB 数据集的加载为例：

total_words = 10000 # 设定词汇量大小
max_review_len = 80 # 最大句子长度
embedding_len = 100 # 词向量长度
# 加载 IMDB 数据集
(x_train, y_train), (x_test, y_test) =keras.datasets.imdb.load_data(num_words=total_words)
# 将句子填充或截断到相同长度，设置为末尾填充和末尾截断方式
x_train = keras.preprocessing.sequence.pad_sequences(
x_train,maxlen=max_review_len,truncating='post',padding='post')

x_test = keras.preprocessing.sequence.pad_sequences(
x_test,maxlen=max_review_len,truncating='post',padding='post')

print(x_train.shape, x_test.shape)

Out[30]: (25000, 80) (25000, 80)

上述代码中，我们将句子的最大长度 max_review_len 设置为 80 个单词，通过keras.preprocessing.sequence.pad_sequences 可以快速完成句子的填充和截断工作，以其中某个句子为例：

[ 1 778 128 74 12 630 163 15 4 1766 7982 1051 2 32
 85 156 45 40 148 139 121 664 665 10 10 1361 173 4
 749 2 16 3804 8 4 226 65 12 43 127 24 2 10
 10 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0]

可以看到在句子末尾填充了若干数量的 0，使得句子的长度刚好 80。实际上，也可以选择句子长度不够时，在句子前面填充 0；句子长度过长时，截断句首的单词。经过处理后，所有的句子长度都变为 80，从而训练集可以保存 shape 为[25000,80]的张量，测试集可以保存 shape 为[25000,80]的张量。

我们介绍对多个维度进行填充的例子。考虑对图片的高宽维度进行填充。以 28x28 大小的图片数据为例，如果网络层所接受的数据高宽为 32x32，则必须将 28x28 大小填充到32x32，可以在上、下、左、右方向各填充 2 个单元，如下图 5.2 所示：

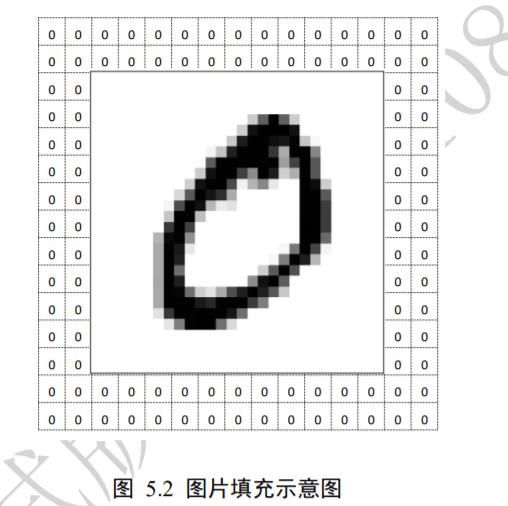
上述填充方案可以表达为[[0,0],[2,2],[2,2],[0,0]]，实现为：

x = tf.random.normal([4,28,28,1])
# 图片上下、左右各填充 2 个单元
tf.pad(x,[[0,0],[2,2],[2,2],[0,0]])

<tf.Tensor: id=16, shape=(4, 32, 32, 1), dtype=float32, numpy=
array([[[[ 0. ],
 [ 0. ],
 [ 0. ],…

通过填充操作后，图片的大小变为 32x32，满足神经网络的输入要求。

5.4.2 复制

在维度变换一节，我们就介绍了通过 tf.tile()函数实现长度为 1 的维度复制的功能。tf.tile 函数除了可以对长度为 1 的维度进行复制若干份，还可以对任意长度的维度进行复制若干份，进行复制时会根据原来的数据次序重复复制。由于已经介绍过，此处仅作简单回顾。

通过 tf.tile 函数可以在任意维度将数据重复复制多份，如 shape 为[4,32,32,3]的数据，复制方案 multiples=[2,3,3,1]，即通道数据不复制，高宽方向分别复制 2 份，图片数再复制1 份:

x = tf.random.normal([4,32,32,3])
tf.tile(x,[2,3,3,1]) # 数据复制

Out[32]:<tf.Tensor: id=25, shape=(8, 96, 96, 3), dtype=float32, numpy=
array([[[[ 1.20957184e+00, 2.82766962e+00, 1.65782201e+00],
 [ 3.85402292e-01, 2.00732923e+00, -2.79068202e-01],
 [-2.52583921e-01, 7.82584965e-01, 7.56870627e-01],...

5.5 数据限幅

考虑怎么实现非线性激活函数 ReLU 的问题。它其实可以通过简单的数据限幅运算实现，限制数据的范围 ∈ [0, +∞)即可。

在 TensorFlow 中，可以通过 tf.maximum(x, a)实现数据的下限幅： ∈ [, +∞)；可以通过 tf.minimum(x, a)实现数据的上限幅： ∈ (−∞,]，举例如下：

x = tf.range(9)
tf.maximum(x,2) # 下限幅 2

Out[33]:<tf.Tensor: id=48, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,
4, 5, 6, 7, 8])>

In [34]:tf.minimum(x,7) # 上限幅 7
Out[34]:<tf.Tensor: id=41, shape=(9,), dtype=int32, numpy=array([0, 1, 2, 3,
4, 5, 6, 7, 7])>

那么 ReLU 函数可以实现为：

def relu(x):
 return tf.minimum(x,0.) # 下限幅为 0 即可

通过组合 tf.maximum(x, a)和 tf.minimum(x, b)可以实现同时对数据的上下边界限幅： ∈ [, ]:

x = tf.range(9)
tf.minimum(tf.maximum(x,2),7) # 限幅为 2~7

Out[35]:<tf.Tensor: id=57, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,
4, 5, 6, 7, 7])>

更方便地，我们可以使用 tf.clip_by_value 实现上下限幅：

x = tf.range(9)
tf.clip_by_value(x,2,7) # 限幅为 2~7

Out[36]:<tf.Tensor: id=66, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,
4, 5, 6, 7, 7])>

5.6 高级操作

上述介绍的操作函数大部分都是常有并且容易理解的，接下来我们将介绍部分常用，但是稍复杂的功能函数。

5.6.1 tf.gather

tf.gather 可以实现根据索引号收集数据的目的。考虑班级成绩册的例子，共有 4 个班级，每个班级 35 个学生，8 门科目，保存成绩册的张量 shape 为[4,35,8]。

x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32)

现在需要收集第 1-2 个班级的成绩册，可以给定需要收集班级的索引号：[0,1]，班级的维度 axis=0:

tf.gather(x,[0,1],axis=0) # 在班级维度收集第 1-2 号班级成绩册

Out[38]:<tf.Tensor: id=83, shape=(2, 35, 8), dtype=int32, numpy=
array([[[43, 10, 93, 85, 75, 87, 28, 19],
 [52, 17, 44, 88, 82, 54, 16, 65],
 [98, 26, 1, 47, 59, 3, 59, 70],…

实际上，对于上述需求，通过切片[: 2]可以更加方便地实现。但是对于不规则的索引方式，比如，需要抽查所有班级的第 1,4,9,12,13,27 号同学的成绩，则切片方式实现起来非常麻烦，而 tf.gather 则是针对于此需求设计的，使用起来非常方便：

# 收集第 1,4,9,12,13,27 号同学成绩
tf.gather(x,[0,3,8,11,12,26],axis=1)

Out[39]:<tf.Tensor: id=87, shape=(4, 6, 8), dtype=int32, numpy=
array([[[43, 10, 93, 85, 75, 87, 28, 19],
 [74, 11, 25, 64, 84, 89, 79, 85],…

如果需要收集所有同学的第 3，5 等科目的成绩，则可以：

tf.gather(x,[2,4],axis=2) # 第 3，5 科目的成绩

Out[40]:<tf.Tensor: id=91, shape=(4, 35, 2), dtype=int32, numpy=
array([[[93, 75],
 [44, 82],
 [ 1, 59],…

可以看到，tf.gather 非常适合索引没有规则的场合，其中索引号可以乱序排列，此时收集的数据也是对应顺序：

a=tf.range(8)
a=tf.reshape(a,[4,2]) # 生成张量 a

Out[41]:<tf.Tensor: id=115, shape=(4, 2), dtype=int32, numpy=
array([[0, 1],
 [2, 3],
 [4, 5],
 [6, 7]])>
 
tf.gather(a,[3,1,0,2],axis=0) # 收集第 4,2,1,3 号元素
Out[42]:<tf.Tensor: id=119, shape=(4, 2), dtype=int32, numpy=
array([[6, 7],
 [2, 3],
 [0, 1],
 [4, 5]])>

我们将问题变得复杂一点：如果希望抽查第[2,3]班级的第[3,4,6,27]号同学的科目成绩，则可以通过组合多个 tf.gather 实现。首先抽出第[2,3]班级：

students=tf.gather(x,[1,2],axis=0) # 收集第 2,3 号班级

<tf.Tensor: id=227, shape=(2, 35, 8), dtype=int32, numpy=
array([[[ 0, 62, 99, 7, 66, 56, 95, 98],…

再从这 2 个班级的同学中提取对应学生成绩：

tf.gather(students,[2,3,5,26],axis=1) # 收集第 3,4,6,27 号同学

Out[44]:<tf.Tensor: id=231, shape=(2, 4, 8), dtype=int32, numpy=
array([[[69, 67, 93, 2, 31, 5, 66, 65], …

此时得到这 2 个班级 4 个同学的成绩，shape 为[2,4,8]。

我们再将问题进一步复杂：这次我们希望抽查第 2 个班级的第 2 个同学的所有科目，第 3 个班级的第 3 个同学的所有科目，第 4 个班级的第 4 个同学的所有科目。那么怎么实现呢？

可以通过笨方式一个一个的手动提取：首先提取第一个采样点的数据：[1,1],可得到8 门科目的数据向量：

x[1,1] # 收集第 2 个班级的第 2 个同学

Out[45]:<tf.Tensor: id=236, shape=(8,), dtype=int32, numpy=array([45, 34,
99, 17, 3, 1, 43, 86])>

再串行提取第二个采样点的数据：[2,2]，和第三个采样点的数据[3,3]，最后通过 stack
方式合并采样结果：

In [46]: tf.stack([x[1,1],x[2,2],x[3,3]],axis=0)
Out[46]:<tf.Tensor: id=250, shape=(3, 8), dtype=int32, numpy=
array([[45, 34, 99, 17, 3, 1, 43, 86],
 [11, 25, 84, 95, 97, 95, 69, 69],
 [ 0, 89, 52, 29, 76, 7, 2, 98]])>

这种方法也能正确的得到 shape 为[3,8]的结果，其中 3 表示采样点的个数，4 表示每个采样点的数据。但是它最大的问题在于手动串行方式执行采样，计算效率极低。有没有更好的方式实现呢？这就是下一节要介绍的 tf.gather_nd 的功能。

5.6.2 tf.gather_nd

通过 tf.gather_nd，可以通过指定每次采样的坐标来实现采样多个点的目的。

回到上面的挑战，我们希望抽查第 2 个班级的第 2 个同学的所有科目，第 3 个班级的第 3 个同学的所有科目，第 4 个班级的第 4 个同学的所有科目。
那么这 3 个采样点的索引坐标可以记为:[1,1],[2,2],[3,3]，我们将这个采样方案合并为一个 List 参数：[[1,1],[2,2],[3,3]]，通过tf.gather_nd 实现如下：

# 根据多维度坐标收集数据
tf.gather_nd(x,[[1,1],[2,2],[3,3]])

Out[47]:<tf.Tensor: id=256, shape=(3, 8), dtype=int32, numpy=
array([[45, 34, 99, 17, 3, 1, 43, 86],
 [11, 25, 84, 95, 97, 95, 69, 69],
 [ 0, 89, 52, 29, 76, 7, 2, 98]])>

可以看到，结果与串行采样完全一致，实现更加简洁，计算效率大大提升。

一般地，在使用 tf.gather_nd 采样多个样本时，如果希望采样第 i 号班级，第 j 个学生，第 k 门科目的成绩，则可以表达为[. . . ,[,, ], . . .]，外层的括号长度为采样样本的个数，内层列表包含了每个采样点的索引坐标：

# 根据多维度坐标收集数据
tf.gather_nd(x,[[1,1,2],[2,2,3],[3,3,4]])

Out[48]:<tf.Tensor: id=259, shape=(3,), dtype=int32, numpy=array([99, 95,
76])>

上述代码中，我们抽出了班级 1，学生 1 的科目 2；班级 2，学生 2 的科目 3；班级 3，学生 3 的科目 4 的成绩，共有 3 个成绩数据，结果汇总为一个 shape 为[3]的张量。

5.6.3 tf.boolean_mask

除了可以通过给定索引号的方式采样，还可以通过给定掩码(mask)的方式采样。继续以 shape 为[4,35,8]的成绩册为例，这次我们以掩码方式进行数据提取。考虑在班级维度上进行采样，对这 4 个班级的采样方案的掩码为

= [, , , ]

即采样第 1 和第 4 个班级，通过 tf.boolean_mask(x, mask, axis)可以在 axis 轴上根据 mask 方案进行采样，实现为：

# 根据掩码方式采样班级
tf.boolean_mask(x,mask=[True, False,False,True],axis=0)

<tf.Tensor: id=288, shape=(2, 35, 8), dtype=int32, numpy=
array([[[43, 10, 93, 85, 75, 87, 28, 19],…

注意掩码的长度必须与对应维度的长度一致，如在班级维度上采样，则必须对这 4 个班级是否采样的掩码全部指定，掩码长度为 4。

如果对 8 门科目进行掩码采样，设掩码采样方案为:

= [, , , , , , , ]

则可以实现为：

# 根据掩码方式采样科目
tf.boolean_mask(x,mask=[True,False,False,True,True,False,False,True],axis=2)

<tf.Tensor: id=318, shape=(4, 35, 4), dtype=int32, numpy=
array([[[43, 85, 75, 19],…

不难发现，这里的 tf.boolean_mask 的用法其实与 tf.gather 非常类似，只不过一个通过掩码方式采样，一个直接给出索引号采样。

现在我们来考虑与 tf.gather_nd 类似方式的多维掩码采样方式。为了方便演示，我们将班级数量减少到 2 个，学生的数量减少到 3 个，即一个班级只有 3 个学生，shape 为[2,3,8]。

如果希望采样第 1 个班级的第 1-2 号学生，第 2 个班级的第 2-3 号学生，通过tf.gather_nd 可以实现为：

x = tf.random.uniform([2,3,8],maxval=100,dtype=tf.int32)
tf.gather_nd(x,[[0,0],[0,1],[1,1],[1,2]]) # 多维坐标采集

<tf.Tensor: id=325, shape=(4, 8), dtype=int32, numpy=
array([[52, 81, 78, 21, 50, 6, 68, 19],
 [53, 70, 62, 12, 7, 68, 36, 84],
 [62, 30, 52, 60, 10, 93, 33, 6],
 [97, 92, 59, 87, 86, 49, 47, 11]])>

共采样 4 个学生的成绩，shape 为[4,8]。

如果用掩码方式，怎么表达呢？如下表格 5.2 所示，行为每个班级，列为对应学生，表中数据表达了对应位置的采样情况：

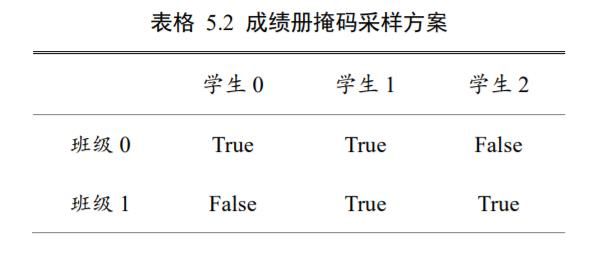
因此，通过这张表，就能很好地表征利用掩码方式的采样方案：

# 多维掩码采样
tf.boolean_mask(x,[[True,True,False],[False,True,True]])

<tf.Tensor: id=354, shape=(4, 8), dtype=int32, numpy=
array([[52, 81, 78, 21, 50, 6, 68, 19],
 [53, 70, 62, 12, 7, 68, 36, 84],
 [62, 30, 52, 60, 10, 93, 33, 6],
 [97, 92, 59, 87, 86, 49, 47, 11]])>

采样结果与 tf.gather_nd 完全一致。可见 tf.boolean_mask既可以实现了tf.gather 方式的一维掩码采样，又可以实现 tf.gather_nd 方式的多维掩码采样。

上面的 3 个操作比较常用，尤其是 tf.gather 和 tf.gather_nd 出现的频率较高，必须掌握。下面再补充 3 个高阶操作。

5.6.4 tf.where

通过 tf.where(cond, a, b)操作可以根据 cond 条件的真假从 a 或 b 中读取数据，条件判定规则如下：

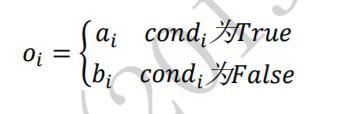
其中 i 为张量的索引，返回张量大小与 a,b 张量一致，当对应位置中 $cond_{i}$ 为 True， $o_{i}$ 位置从 $a_{i}$ 中复制数据；当对应位置中 $cond_{i}$ 为 False， $o_{i}$ 位置从 $b_{i}$ 中复制数据。

考虑从 2 个全 1、全 0 的 3x3 大小的张量 a,b 中提取数据，其中 cond 为 True 的位置从 a 中对应位置提取，cond 为 False 的位置从 b 对应位置提取：

a = tf.ones([3,3]) # 构造 a 为全 1
b = tf.zeros([3,3]) # 构造 b 为全 0
# 构造采样条件
cond =tf.constant([[True,False,False],[False,True,False],[True,True,False]])
tf.where(cond,a,b) # 根据条件从 a,b 中采样

Out[53]:<tf.Tensor: id=384, shape=(3, 3), dtype=float32, numpy=
array([[1., 0., 0.],
 [0., 1., 0.],
 [1., 1., 0.]], dtype=float32)>

可以看到，返回的张量中为 1 的位置来自张量 a，返回的张量中为 0 的位置来自张量 b。当 a=b=None 即 a,b 参数不指定时，tf.where 会返回 cond 张量中所有 True 的元素的索引坐标。考虑如下 cond 张量：

cond # 构造 cond
Out[54]:<tf.Tensor: id=383, shape=(3, 3), dtype=bool, numpy=
array([[ True, False, False],
 [False, True, False],
 [ True, True, False]])>

其中 True 共出现 4 次，每个 True 位置处的索引分布为[0,0