python实现logistic增长模型拟合2019-nCov确诊人数
背景:众志成城抗疫情。今天是2020年1月28日,2019-nCov确诊人数一直在增长趋势,如何更好的对确诊人数进行拟合和预测,需要我们用python来实现。注意,本文模型为logistic增长模型,并非最佳预测模型,只是大致预测,对之前的感染人数曲线进行拟合,以后的疫情发展情况还是需要根据实际情况得出。模型根据2020年1月28日及之前的数据进行拟合,后续可能会更新。
目录
一、logistic增长
1.1 J型增长和S型增长
1.2 logistic增长函数
二、python对函数曲线的拟合
2.1 定义散点坐标
2.2 用最小二乘法进行拟合
三、疾病下步发展估计
3.1 不加人为干预
3.2 乐观预计模型
3.3 最乐观预计模型
3.4 停止增长时间
四、全部代码
一、logistic增长
1.1 J型增长和S型增长
指数增长,J型曲线:指数增长,即增长不受抑制,呈爆炸式的。
比如一个人可以传染三个人,三个人传染九个人,九个人传染27个人,不停的倍增。这就是J型增长,也叫指数型的增长。
一些传染病初期可能呈现指数增长。
但是实际的增长过程中,增长速率并不能一直维持不变,随着人数的不断增多,增长率会逐渐受到抑制。这就是S型增长。
一般疾病的传播是S型增长的过程,因为疾病传播的过程中会受到一定的阻力。
1.2 logistic增长函数
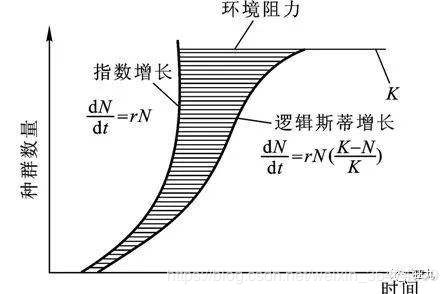
当一个物种迁入到一个新生态系统中后,其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量,则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足(非理想环境),则增长函数满足逻辑斯谛方程,图像呈S形,此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。在以下内容中将具体介绍逻辑斯谛方程的原理、生态学意义及其应用。逻辑斯蒂模型的微分式是:dx/dt=rx(1-x) 式中的r为速率参数。
- K为环境容量,即增长到最后,P(t)能达到的极限。
- P0为初始容量,就是t=0时刻的数量。
- r为增长速率,r越大则增长越快,越快逼近K值,r越小增长越慢,越慢逼近K值。
该公式用python写成函数形式就是:
def logistic_increase_function(t,K,P0,r):
# t:time t0:initial time P0:initial_value K:capacity r:increase_rate
exp_value=np.exp(r*(t-t0))
return (K*exp_value*P0)/(K+(exp_value-1)*P0)logistic增长的曲线也称为s型曲线。下图左图为曲线数量,右图为增长速率。
二、python对函数曲线的拟合
如何用python对任意数据用任意函数的图像进行拟合:
https://blog.csdn.net/changdejie/article/details/83089933
2.1 定义散点坐标
定义是当日24时的累积确诊人数,没有详细考证,可能有出入。
'''
1.11日41例
1.18日45例
1.19日62例
1.20日291例
1.21日440例
1.22日571例
1.23日830例
1.24日1287例
1.25日1975例
1.26日2744例
1.27日4515例
'''
t=[11,18,19,20 ,21, 22, 23, 24, 25, 26, 27]
t=np.array(t)
P=[41,45,62,291,440,571,830,1287,1975,2744,4515]
P=np.array(P)2.2 用最小二乘法进行拟合
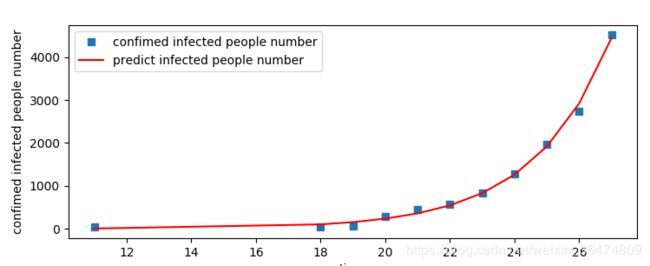
最小二乘法,对logistic增长函数进行拟合。
# 用最小二乘法估计拟合
popt, pcov = curve_fit(logistic_increase_function, t, P)
#获取popt里面是拟合系数
print("K:capacity P0:initial_value r:increase_rate t:time")
print(popt)
#拟合后预测的P值
P_predict = logistic_increase_function(t,popt[0],popt[1],popt[2])
#未来预测
future=[11,18,19,20 ,21, 22, 23, 24, 25, 26, 27,28,29,30,31,41,51,61,71,81,91,101]
future=np.array(future)
future_predict=logistic_increase_function(future,popt[0],popt[1],popt[2])
#近期情况预测
tomorrow=[28,29,30,32,33,35,37,40]
tomorrow=np.array(tomorrow)
tomorrow_predict=logistic_increase_function(tomorrow,popt[0],popt[1],popt[2])
#绘图
plot1 = plt.plot(t, P, 's',label="confimed infected people number")
plot2 = plt.plot(t, P_predict, 'r',label='predict infected people number')
plot3 = plt.plot(tomorrow, tomorrow_predict, 'b',label='predict infected people number')
plt.xlabel('time')
plt.ylabel('confimed infected people number')
plt.legend(loc=0) #指定legend的位置右下角
print(logistic_increase_function(np.array(28),popt[0],popt[1],popt[2]))
print(logistic_increase_function(np.array(29),popt[0],popt[1],popt[2]))
plt.show()三、疾病下步发展估计
3.1 不加人为干预
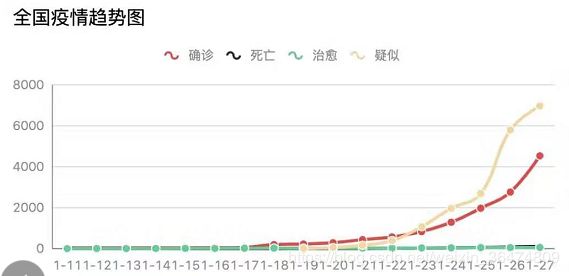
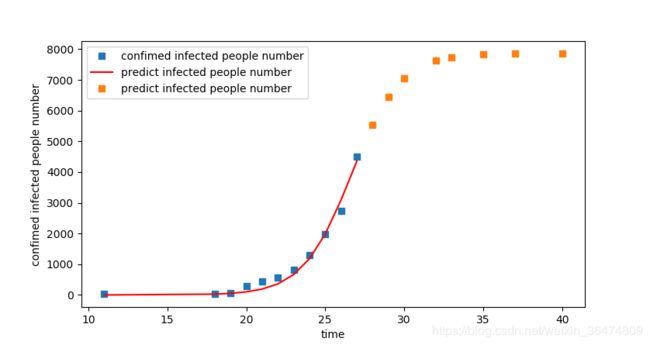
红色曲线为丁香医生统计的实际感染人数曲线,下方图片为博主用最小二乘法用logistic函数增长拟合的,最终
K,P0,r的值分别为[4.01665705e+10 5.36213622e+00 4.19963424e-01]
照此趋势增长下去,最终K=4.01665705e+10人会被感染,显然不可能。
此模型预测出明日1月28日24点感染人数累计6759人,1月29日24点累计感染人数10287人
3.2 乐观预计模型
人为干预后,疾病降低K值,因此可以将r值提升,以加快达到K值的速度。
r取0.55
明日1月28日凌晨24时累计确诊5976,后日1日29日凌晨24时累计确诊7533人,最终感染人数收敛在12000人左右。
3.3 最乐观预计模型
即疾病快速逼近K值,r=0.65,
明日1月28日凌晨24时累计确诊5533,后日1日29日凌晨24时累计确诊6445人,最终感染人数收敛在8000人左右。
3.4 停止增长时间
按模型预计,2月5日左右确诊感染人数能停止增长。
保持乐观心态,积极预防,总会战胜新型冠状病毒。
四、全部代码
#!/usr/bin/python
# -*- coding: UTF-8 -*-
"""
拟合2019-nCov肺炎感染确诊人数
"""
import numpy as np
import matplotlib.pyplot as plt
import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def logistic_increase_function(t,K,P0,r):
t0=11
r=0.65
# r = 0.55
# t:time t0:initial time P0:initial_value K:capacity r:increase_rate
exp_value=np.exp(r*(t-t0))
return (K*exp_value*P0)/(K+(exp_value-1)*P0)
'''
1.11日41例
1.18日45例
1.19日62例
1.20日291例
1.21日440例
1.22日571例
1.23日830例
1.24日1287例
1.25日1975例
1.26日2744例
1.27日4515例
'''
# 日期及感染人数
t=[11,18,19,20 ,21, 22, 23, 24, 25, 26, 27]
t=np.array(t)
P=[41,45,62,291,440,571,830,1287,1975,2744,4515]
P=np.array(P)
# 用最小二乘法估计拟合
popt, pcov = curve_fit(logistic_increase_function, t, P)
#获取popt里面是拟合系数
print("K:capacity P0:initial_value r:increase_rate t:time")
print(popt)
#拟合后预测的P值
P_predict = logistic_increase_function(t,popt[0],popt[1],popt[2])
#未来预测
future=[11,18,19,20 ,21, 22, 23, 24, 25, 26, 27,28,29,30,31,41,51,61,71,81,91,101]
future=np.array(future)
future_predict=logistic_increase_function(future,popt[0],popt[1],popt[2])
#近期情况预测
tomorrow=[28,29,30,32,33,35,37,40]
tomorrow=np.array(tomorrow)
tomorrow_predict=logistic_increase_function(tomorrow,popt[0],popt[1],popt[2])
#绘图
plot1 = plt.plot(t, P, 's',label="confimed infected people number")
plot2 = plt.plot(t, P_predict, 'r',label='predict infected people number')
plot3 = plt.plot(tomorrow, tomorrow_predict, 's',label='predict infected people number')
plt.xlabel('time')
plt.ylabel('confimed infected people number')
plt.legend(loc=0) #指定legend的位置右下角
print(logistic_increase_function(np.array(28),popt[0],popt[1],popt[2]))
print(logistic_increase_function(np.array(29),popt[0],popt[1],popt[2]))
plt.show()
#未来预测绘图
#plot2 = plt.plot(t, P_predict, 'r',label='polyfit values')
#plot3 = plt.plot(future, future_predict, 'r',label='polyfit values')
#plt.show()
print("Program done!")
博客文章总目录-邢翔瑞的技术博客
支持向量机(Support Vector Machine,SVM)算法复杂度详解
谷歌论文Weight Agnostic Neural Networks(WANN)权重无关神经网络
王者荣耀中的数学原理及游戏策略(一)防御篇(护甲|魔抗|伤害运算机制)