傅里叶变换及高低通滤波器的分类(均值滤波,高斯滤波,sobel,scharr,拉普拉斯滤波器)
高通滤波,低通滤波是按频率划分的。对于正弦曲线,振幅变化快就是高频,变化慢就是低频。那么对于图像,像素值变化快就是高频(噪声啦,边缘啦、边缘及噪声在局部像素值变化较大),像素值变化慢就是低频。所以一幅图像低频较多,高频较少。那么保留高频就是高通滤波器(边缘提取),保留低频就是低通录波器(图像平滑)。
傅里叶变换将图像转换成幅值谱(magnitude_spectrum):按频率从小到大由中心向四周扩散,幅值谱越亮说明像素越多,反之则越少。
那么一幅图像经过傅里叶变换之后一定是中心较亮,四周较暗(低频像素多,高频像素少),上代码:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread('../images/example_01.jpg',0)
# 高通滤波 numpy 用的多
# 正变换
f=np.fft.fft2(img)
fshift=np.fft.fftshift(f)
magnitude_spectrum=20*np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(img,cmap='gray'),plt.title('Input Image'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum,cmap='gray'),plt.title('magnitude_spectrum')
plt.show()
import cv2
import numpy as np
import matplotlib.pyplot as plt
# img=cv2.imread('../images/can.jpg',0)
# img=cv2.imread('../images/qin.jpg',0)
img=cv2.imread('../images/example_01.jpg',0)
# 高通滤波 numpy 用的多
# 正变换
f=np.fft.fft2(img)
fshift=np.fft.fftshift(f)
magnitude_spectrum=20*np.log(np.abs(fshift))
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2)
print('img.shape',img.shape)
# 低频过滤
fshift[(crow-30):(crow+30),(ccol-30):(ccol+30)]=0
#逆变换
f_ishift=np.fft.ifftshift(fshift)
img_back=np.abs(np.fft.ifft2(f_ishift))
plt.subplot(121),plt.imshow(img,cmap='gray'),plt.title('Input Image'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(img_back,cmap='gray'),plt.title('img_back'),plt.xticks([]),plt.yticks([])
plt.show()
上效果:

那么均值滤波,高斯滤波,sobel,scharr,拉普拉斯滤波器是低通滤波器还高通滤波器呢?我们通过幅值谱来判
断,上代码:
import cv2
import numpy as np
from matplotlib import pyplot as plt
# simple averaging filter without scaling parameter
# 低通
mean_filter = np.ones((3,3))
# creating a guassian filter
# 低通
x = cv2.getGaussianKernel(5,10)
gaussian = x*x.T
# different edge detecting filters
# scharr in x-direction
# 高通
scharr = np.array([[-3, 0, 3],
[-10,0,10],
[-3, 0, 3]])
# sobel in x direction
# 高通
sobel_x= np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
# sobel in y direction
# 高通
sobel_y= np.array([[-1,-2,-1],
[0, 0, 0],
[1, 2, 1]])
# laplacian
# 高通
laplacian=np.array([[0, 1, 0],
[1,-4, 1],
[0, 1, 0]])
filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \
'sobel_y', 'scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
for i in range(6):
plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()
上效果:
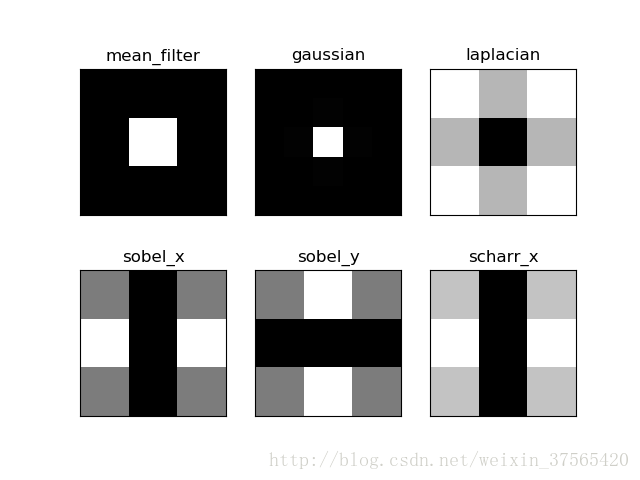
前面讨论过,幅值谱中间为低频,四周为高频且越亮像素越多,就是被滤波器保存下来了。不难发现,均值与高斯滤波器幅值谱中间亮,为低通滤波器(平滑),拉普拉斯、sobel、scharr四周较亮为高通滤波器(边缘提取),边缘提取又分垂直边缘与水平边缘~这个从图上看就一目了然啦。
傅里叶变换将图像转换成幅值谱(magnitude_spectrum):按频率从小到大由中心向四周扩散,幅值谱越亮说明像素越多,反之则越少。
那么一幅图像经过傅里叶变换之后一定是中心较亮,四周较暗(低频像素多,高频像素少),上代码:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread('../images/example_01.jpg',0)
# 高通滤波 numpy 用的多
# 正变换
f=np.fft.fft2(img)
fshift=np.fft.fftshift(f)
magnitude_spectrum=20*np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(img,cmap='gray'),plt.title('Input Image'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum,cmap='gray'),plt.title('magnitude_spectrum')
plt.show()
上效果:
那么像提取图像的边缘就是去掉低频保留高频:先通过傅里叶正变换得到幅值谱,去掉低频像素,然后再通过傅里叶逆变换得到图像边缘。上代码:import cv2
import numpy as np
import matplotlib.pyplot as plt
# img=cv2.imread('../images/can.jpg',0)
# img=cv2.imread('../images/qin.jpg',0)
img=cv2.imread('../images/example_01.jpg',0)
# 高通滤波 numpy 用的多
# 正变换
f=np.fft.fft2(img)
fshift=np.fft.fftshift(f)
magnitude_spectrum=20*np.log(np.abs(fshift))
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2)
print('img.shape',img.shape)
# 低频过滤
fshift[(crow-30):(crow+30),(ccol-30):(ccol+30)]=0
#逆变换
f_ishift=np.fft.ifftshift(fshift)
img_back=np.abs(np.fft.ifft2(f_ishift))
plt.subplot(121),plt.imshow(img,cmap='gray'),plt.title('Input Image'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(img_back,cmap='gray'),plt.title('img_back'),plt.xticks([]),plt.yticks([])
plt.show()
上效果:

那么均值滤波,高斯滤波,sobel,scharr,拉普拉斯滤波器是低通滤波器还高通滤波器呢?我们通过幅值谱来判
断,上代码:
import cv2
import numpy as np
from matplotlib import pyplot as plt
# simple averaging filter without scaling parameter
# 低通
mean_filter = np.ones((3,3))
# creating a guassian filter
# 低通
x = cv2.getGaussianKernel(5,10)
gaussian = x*x.T
# different edge detecting filters
# scharr in x-direction
# 高通
scharr = np.array([[-3, 0, 3],
[-10,0,10],
[-3, 0, 3]])
# sobel in x direction
# 高通
sobel_x= np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]])
# sobel in y direction
# 高通
sobel_y= np.array([[-1,-2,-1],
[0, 0, 0],
[1, 2, 1]])
# laplacian
# 高通
laplacian=np.array([[0, 1, 0],
[1,-4, 1],
[0, 1, 0]])
filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian','laplacian', 'sobel_x', \
'sobel_y', 'scharr_x']
fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]
for i in range(6):
plt.subplot(2,3,i+1),plt.imshow(mag_spectrum[i],cmap = 'gray')
plt.title(filter_name[i]), plt.xticks([]), plt.yticks([])
plt.show()
上效果:

前面讨论过,幅值谱中间为低频,四周为高频且越亮像素越多,就是被滤波器保存下来了。不难发现,均值与高斯滤波器幅值谱中间亮,为低通滤波器(平滑),拉普拉斯、sobel、scharr四周较亮为高通滤波器(边缘提取),边缘提取又分垂直边缘与水平边缘~这个从图上看就一目了然啦。
