一文详尽混淆矩阵、准确率、精确率、召回率、F1值、P-R 曲线、ROC 曲线、AUC 值、Micro-F1 和 Macro-F1
文章目录
- 二分类的评价指标
- 一、混淆矩阵与 TP、TN、FP、FN
- 二、准确率、精确率、召回率、F1值
- 三、P-R 曲线
- 四、ROC 曲线、AUC 值
- 五、P-R曲线和ROC曲线有什么区别,如何选择?
- 多分类的评价指标
- References
二分类的评价指标
对于二分类问题,机器预测的和实际的还是会有所偏差,所以我们引入以下几个概念来评价分类器的优良。
一、混淆矩阵与 TP、TN、FP、FN
混淆矩阵
| 预测的类 | ||||
| 正类 | 负类 | 合计 | ||
| 实际的类 | 正样本 | TP | FN | P |
| 负样本 | FP | TN | N | |
| 合计 | P’ | N’ | P+N | |
T,True;F,False;P,Positive;N,Negative
TP:真阳,将正样本判断为正类。注:阳,意动用法,认为…是阳性。真阳,即判断样本为阳性是正确的。
TN:真阴,将负样本判断为负类。
FP:假阳,将负样本判断为正类。
FN:假阴,将正样本判断为负类。
P:正样本个数 = TP + FN
N:负样本个数
P’:被分类器分为正元组的样本数。
N’:被分类器分为负元组的样本数。
S:总预测样本个数 = P + N = P‘ + N’
二、准确率、精确率、召回率、F1值
首先介绍三个指标。
- 准确率(Accuracy)。顾名思义,就是所有的预测正确(正类负类)的占总预测样本个数(S)的比重。
A c c u r a c y = T P + T N S Accuracy = \frac{TP+TN}{S} Accuracy=STP+TN
- 精确率(Precision),查准率。即正确预测为正的占全部预测为正的比例。
P r e c i s i o n = T P P ′ Precision = \frac{TP}{P'} Precision=P′TP
- 召回率(Recall),查全率。即正确预测为正的占全部实际为正的比例。
R e c a l l = T P P Recall = \frac{TP}{P} Recall=PTP
深入理解:召回率与精确率用于衡量分类器的漏报(弃真)和虚警(取伪)比例。精确率越低,则虚警的可能性越大。一般在生活中,弃真的后果比取伪严重得多,例如医生诊断病人是否患有肺炎(COVID-19),取伪,也就是虚惊一场,弃真这可就严重了。也就是说,要尽量降低弃真的可能,也就是提高召回率。换而言之,一般情况下,召回率比精确率重要。但只是一般情况,召回率、精确率哪个更重要还是取决于具体应用场景。
查准率(精确率)可以认为是”宁缺毋滥”,适合对准确率要求高的应用,例如商品推荐,网页检索等。查全率(召回率)可以认为是”宁错杀一百,不放过1个”,适合类似于检查走私、逃犯信息等。
人们通常使用准确率和召回率这两个指标,来评价二分类模型的分析效果。
但是当这两个指标发生冲突时,如何权衡?例如以下,A、B 两个模型哪个的综合性能更优?
| 准确率 | 召回率 | |
|---|---|---|
| A 模型 | 80% | 90% |
| B 模型 | 90% | 80% |
为了解决这个问题,人们提出了 F β F_\beta Fβ 分数。
F β F_\beta Fβ 的物理意义就是将准确率和召回率这两个分值合并为一个分值,在合并的过程中,召回率的权重是准确率的 β \beta β倍。即 W R = β ⋅ W P W_R = \beta\cdot W_P WR=β⋅WP . 则
F β = ( 1 + β 2 ) ⋅ precision ⋅ recall ( β 2 ⋅ precision ) + recall F_{\beta}=\left(1+\beta^{2}\right) \cdot \frac{\text { precision } \cdot \text {recall}}{\left(\beta^{2} \cdot \text { precision }\right)+\text {recall}} Fβ=(1+β2)⋅(β2⋅ precision )+recall precision ⋅recall
F 1 F_1 F1 分数( F 1 S c o r e F_1\ Score F1 Score )认为召回率和准确率同等重要, F 2 F_2 F2 分数认为召回率的重要程度是准确率的2倍,而 F 0.5 F_{0.5} F0.5 分数认为召回率的重要程度是准确率的一半。
当 β = 1 \beta=1 β=1 时,
F 1 = precision ⋅ recall 0.5 ⋅ ( precision + recall) F_{1}= \frac{\text { precision } \cdot \text {recall}}{ 0.5 \cdot(\text { precision }+\text {recall)}} F1=0.5⋅( precision +recall) precision ⋅recall
2 F 1 = 1 P r e c i s i o n + 1 R e c a l l \frac{2}{F_1}=\frac{1}{Precision}+\frac{1}{Recall} F12=Precision1+Recall1
F1 值是P、R的调和平均数,为算数平均数除以几何平均数,且越大越好。
三、P-R 曲线
如果有个划分点可以把正负样本完全区分开,那么P-R曲线就是整个1*1的面积。此时的二分类模型是最完美的。
总之,P-R曲线应该是从(0,0)开始画的一条曲线,切割1*1的正方形,得到一块区域。
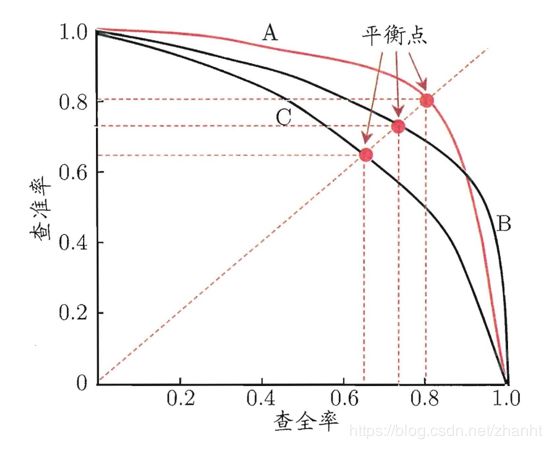
在进行比较时,若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全“包住”,则B的性能优于A。但是两个学习器的P-R曲线往往会发生交叉。这时候如何根据P-R曲线比较两个学习器的性能?(其实就是 Precision 和 Recall 率的权衡)
1、平衡点(BEP):我们认为平衡点越靠近(1,1)则性能越好。
2、 F 1 F_1 F1 度量
3、 F β F_β Fβ 度量
不再赘述。
四、ROC 曲线、AUC 值
首先引入两个指标,灵敏度和 1-特异度。
灵敏度(True Positive Rate,TPR)其实就是召回率,公式如下
TPR = T P T P + F N {\text { TPR }=\frac{T P}{T P+F N}} \\ TPR =TP+FNTP
1-特异度(False Positive Rate,FPR)是错判负样本为正类占所有负样本的比例,公式如下:
FPR = F P F P + T N {\text {FPR}=\frac{F P}{F P+T N}} FPR=FP+TNFP
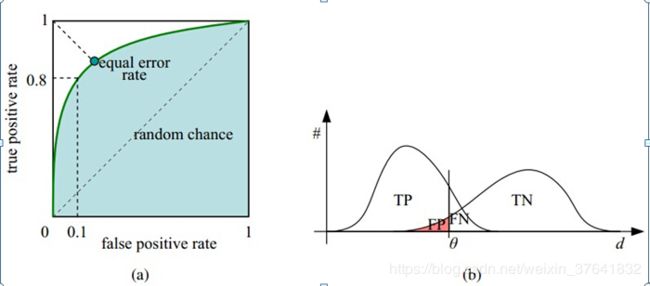
以 TPR 为纵轴,以 FPR 为横轴,画出 ROC 曲线,ROC 曲线下的面积就是 AUC(Area under Curve)。从 FPR 和 TPR 的定义可以理解,TPR 越高,FPR 越小,我们的模型的性能也就越好。也就是说,ROC 曲线越靠近左上角 (1, 1) 模型越好。
AUC 是一个模型评价指标,用于二分类模型的评价。
为什么要用AUC作为二分类模型的评价指标呢?为什么不直接通过计算准确率来对模型进行评价呢?答案是这样的:机器学习中的很多模型对于分类问题的预测结果大多是概率,即属于某个类别的概率,如果计算准确率的话,就要把概率转化为类别,这就需要设定一个阈值,概率大于某个阈值的属于一类,概率小于某个阈值的属于另一类,而**阈值的设定直接影响了准确率的计算。**见下图(b)
AUC值。AUC (Area Under Curve) 被定义为ROC曲线下的面积。
显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间。
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
从AUC判断分类器(预测模型)优劣的标准:
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
一句话来说,AUC值越大的分类器,正确率越高。
五、P-R曲线和ROC曲线有什么区别,如何选择?
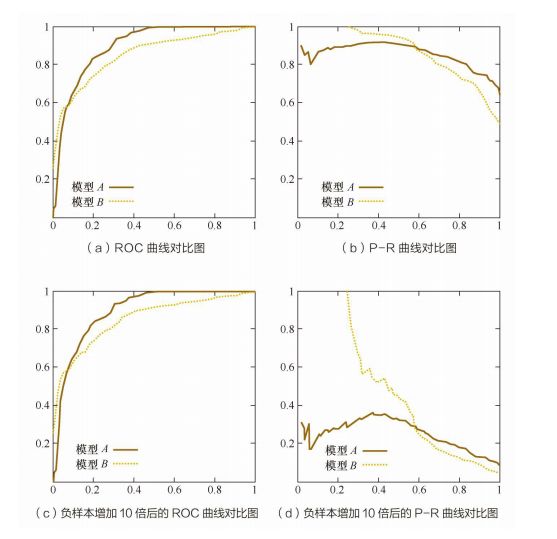
图 a) 和 b) 是原始样本的 ROC曲线和 PR曲线,
图 c) 和 d) 则是将负样本增加10倍后的 ROC曲线和 PR曲线。
1)从 a 和 c 可以看出,负样本增加10倍后,ROC曲线变化不大。分析一下为什么变化不大,其Y轴是TPR,x轴是FPR,当固定一个threshold来计算TPR和FPR的时候,虽然负样本增加了10倍,也就是FPR的分母虽然变大了,但是正常概率来讲,这个时候超过threshold的负样本量也会随之增加,也就是分子也会随之增加,所以总体FPR变化不大,从这个角度来看的话正负样本稍微不均衡的话,对KS影响也不大,因为KS=max(TPR-FPR),这个前提是正负样本的量都比较大的情况下,因为只有样本量比较大的情况下,根据大数定律,计算出来的频率才非常接近于真实的概率值,有资料显示正负样本都超过6000的量,计算的频率就比较接近概率。所以在样本量都不是很大的情况下,如果样本还极端不均衡的话,就会有一些影响。由此可见,ROC曲线能够尽量降低不同测试集带来的干扰,更加客观地衡量模型本身的性能。
2)从 b 和 d 图可以看出,负样本增加10倍后,PR 曲线变化比较大。也分析一下为什们变化大,其 Y 轴是precision,x 轴是 recall,当负样本增加10倍后,在 racall 不变的情况下,必然召回了更多的负样本,所以精确度会大幅下降,b和d图示也非常明显的反映了这一状况,所以PR曲线变化很大,所以PR曲线对正负样本分布比较敏感。
如何选择呢?
-
在很多实际问题中,正负样本数量往往很不均衡。比如,计算广告领域经常涉及转化率模型,正样本的数量往往是负样本数量的1/1000,甚至1/10000。若选择不同的测试集,P-R曲线的变化就会非常大,而ROC曲线则能够更加稳定地反映模型本身的好坏。所以,ROC曲线的适用场景更多,被广泛用于排序、推荐、广告等领域。
-
但需要注意的是,选择P-R曲线还是ROC曲线是因实际问题而异的,如果研究者希望更多地看到模型在特定数据集上的表现,P-R曲线则能够更直观地反映其性能。
-
PR曲线比ROC曲线更加关注正样本,而ROC则兼顾了两者。
-
AUC越大,反映出正样本的预测结果更加靠前。(推荐的样本更能符合用户的喜好)
-
当正负样本比例失调时,比如正样本1个,负样本100个,则ROC曲线变化不大,此时用PR曲线更加能反映出分类器性能的好坏。这个时候指的是两个分类器,因为只有一个正样本,所以在画auc的时候变化可能不太大;但是在画PR曲线的时候,因为要召回这一个正样本,看哪个分类器同时召回了更少的负样本,差的分类器就会召回更多的负样本,这样precision必然大幅下降,这样分类器性能对比就出来了。
多分类的评价指标
其实多分类的评价指标的计算方式与二分类完全一样,只不过我们计算的是针对于每一类来说的召回率、精确度、准确率和 F1分数。
对于某一个确定的类别来讲,P 其实就是实际属于这一类中的样本,N 其实就是实际属于其他类的所有样本,P’ 其实就是被分类器分类这一类的所有样本,N’ 就是被分类器分类为其他类的所有样本数。
Micro-F1 和 Macro-F1
最后看Micro-F1和Macro-F1。在第一个多标签分类任务中,可以对每个“类”,计算F1,显然我们需要把所有类的F1合并起来考虑。
这里有两种合并方式:
第一种计算出所有类别总的 Precision和 Recall,然后计算F1。这种方式被称为Micro-F1微平均。
microP = 1 n ∑ 1 n P i microR = 1 n ∑ 1 n R i mircoF 1 = 2 × macroP × macroR macroP + macroR \begin{aligned} &\operatorname{microP}=\frac{1}{n} \sum_{1}^{n} P_{i}\\\\ &\operatorname{microR}=\frac{1}{n} \sum_{1}^{n} R_{i}\\\\ &\operatorname{mircoF} 1=\frac{2 \times \operatorname{macroP} \times \operatorname{macroR}}{\operatorname{macroP}+\operatorname{macroR}} \end{aligned} microP=n11∑nPimicroR=n11∑nRimircoF1=macroP+macroR2×macroP×macroR
第二种方式是计算出每一个类的 Precison 和Recall 后计算F1,最后将F1平均。这种方式叫做Macro-F1宏平均。
microP = T P ‾ T P ‾ × F P ‾ microR = T P ‾ T P ‾ × F N ‾ mircoF 1 = 2 × microP × microR microP + microR \begin{aligned} &\operatorname{microP}=\frac{\overline{T P}}{\overline{T P} \times \overline{F P}}\\\\ &\operatorname{microR}=\frac{\overline{T P}}{\overline{T P} \times \overline{F N}}\\\\ &\operatorname{mircoF} 1=\frac{2 \times \operatorname{microP} \times \operatorname{microR}}{\operatorname{microP}+\operatorname{microR}} \end{aligned} microP=TP×FPTPmicroR=TP×FNTPmircoF1=microP+microR2×microP×microR
References
[1] https://blog.csdn.net/liuningjie1119/article/details/72855114
[2] P-R曲线及与ROC曲线区别
[3] https://blog.csdn.net/CatCherry/article/details/100576677
[4] https://blog.csdn.net/zhihua_oba/article/details/78677469
[5] https://blog.csdn.net/u013063099/article/details/80964865
[6] https://blog.csdn.net/CatCherry/article/details/100576677
[7] 精确率与召回率,RoC 曲线与 PR 曲线