BinaryConnect: Training Deep Neural Networks with binary weights during propagations 论文笔记

0 摘要

    深度神经网络在大量任务中取得了最先进的成果。GPU因为其更快的计算速度，帮助深度网络实现了这些突破。未来，在训练和测试时更快的计算速度对于进一步发展，以及能够在低功耗设备上的消费级别的应用可能至关重要。因此，对深度学习专用硬件的研究和开发展开了新的热潮。二值权重，即仅限于两个可能值（例如-1或1）的权重，通过用简单累加代替许多乘法—累加操作，为专用DL硬件带来巨大便利。因为乘法器在神经网络的数字实现上是空间和功率消耗最高的组件。我们提出BinaryConnect的方法，在训练期间，前向传播和反向传播具有二值化权重的DNN，但是在计算梯度时仍然保持全精度的权重。与dropout方法一样，BinaryConnect也是一种正则化手段。我们通过BinaryConnect，在MNIST，CIFAR-10和SVHN获得近乎最佳的结果。

1 引言

    深度神经网络（DNN）极大地推动了各种任务的发展，特别是在语音识别和计算机视觉领域。最近，深度学习在自然语言处理，尤其是机器翻译方面取得了重大进展。有趣的是，实现这一重大进展的关键因素之一是GPU的出现，速度提升了10到30倍，并且分布式训练。事实上，使用大量的数据来训练更大的模型，在过去几年中取得了突破性进展。今天，研究人员和开发人员设计新的深度学习算法和应用程序往往会发现深受计算能力的限制。与此同时，推动深度学习系统在低功耗设备上的应用（与GPU不同）极大地增加了对深度网络专用硬件研发的兴趣。
    当前CNN网络主要的运算集中在 实数权值乘以实数激活量或者 实数权值乘以实数梯度。本文提出 BinaryConnect 将用于前向传播和后向传播计算的实数权值二值化(-1,1),从而将这些乘法运算变为加减运算。这样即压缩了网络模型大小，有加快速度。下面两条使其具有可行性：
1）足够的精度对于累计和平均大量随机梯度是必须的，但是噪声梯度对于 深度学习主流优化算法的随机梯度下降SGD是可兼容的。SGD通过做出小的噪声尝试来探索参数空间，对于每个权值通过累加随机梯度贡献消除了噪声的影响。所以对于这些累加器保持足够的精度是必须的。
2）噪声权值实际上可以看做一种正则形式，使系统泛化能力更好。

本文贡献：
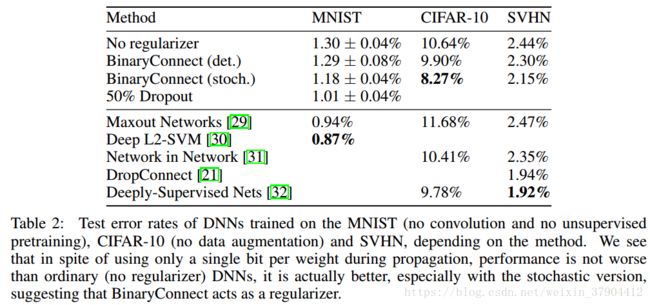
1.尽管模型精度降低了非常多，但是在训练效果却不比全精度的网络差，有的时候二值网络的训练效果甚至会超越全精度网络，因为二值化过程给神经网络带来了noise，像dropout一样，反而是一种regularization，可以部分避免网络的overfitting。
2.二值化网络可以把单精度乘法变成位操作，这大大地减少了训练过程中的运算复杂度。这种位运算可以写成gpu kernel, 或者用fpga实现，会给神经网络训练速度带来提升。
3.存储神经网络模型主要是存储weights. 二值化的weight只要一个bit就可以存下来了，相比之前的32bit，模型减小了32倍，那么把训练好的模型放在移动设备，比如手机上面做测试就比较容易了。

2 BinaryConnect

    在本节中，我们将更详细地介绍BinaryConnect，考虑选择哪两个值，如何离散化，如何训练以及如何进行推理。

2.1 +1 or -1

    DNN主要包括卷积运算和矩阵乘法。 因此，深度学习的关键算法运算是乘法累加操作。人造神经元也是多个累加器，然后计算其输入的加权和。BinaryConnect在传播期间将权重限制为+1或-1。 因此，许多乘法累加操作被简单的加法（和减法）所取代。 这是一个巨大的收益，因为定点加法器在所占的面积和功耗方面比定点乘法累加器少得多。

2.2 确定性与随机二值化

    二值化操作将实值权重转换为两个可能的值。 一个非常简单的二值化操作将基于符号函数：
wb={+1,−1,ifw≥0otherwise(1) w b = { + 1 , i f w ≥ 0 − 1 , o t h e r w i s e ( 1 )
其中， wb w b 是二值化权重， w w 是实值权重。这是一个确定性的二值化操作，另一种替代方案是随机二值化（以一定的概率更新值）：
wb={+1,−1,withprobabilityp=σ(w)withprobability1−p(2) w b = { + 1 , w i t h p r o b a b i l i t y p = σ ( w ) − 1 , w i t h p r o b a b i l i t y 1 − p ( 2 )
其中， σ(x)=clip(x+12,0,1)=max(0,min(1,x+12))(3) σ ( x ) = c l i p ( x + 1 2 , 0 , 1 ) = m a x ( 0 , m i n ( 1 , x + 1 2 ) ) ( 3 )
第二种方法虽然看起来比第一种更合理，但是在实现时却有一个问题，那就是每次生成随机数会非常耗时，所以一般使用第一种方法。

2.3 参数传播与更新

    考虑使用SGD进行反向传播的更新。在这些步骤的每一步中是否仍然行得通。

    关于BinaryConnect的一个关键点是，我们只在前向和后向传播（步骤1和2）期间对权重进行二值化，而不是在参数更新期间（步骤3）进行二值化，如算法1所示。在更新期间保持良好精度的权重对SGD是必不可少的。 两个原因如下：
1.梯度的值的量级很小
2.梯度具有累加效果，即梯度都带有一定的噪音，而噪音一般认为是服从正态分布的，所以，多次累加梯度才能把噪音平均消耗掉。
    另一方面，二值化相当于给权重和激活值添加了噪声，而这样的噪声具有正则化作用，可以防止模型过拟合。所以，二值化也可以被看做是Dropout的一种变形，Dropout是将激活值的一般变成0，从而造成一定的稀疏性，而二值化则是将另一半变成1，从而可以看做是进一步的dropout。

2.4 剪裁

     当实值权重 w w 的变化幅度超过 ±1 ± 1 时，不会影响二值权重的取值（太大的权值对二值参数不产生任何影响）。并且限制权重的幅值也是比较通用的做法。因此，我们将用于参数更新的实数权值取值范围约束在 [−1,1] [ − 1 , 1 ] 之间，其作用是正则化权重。

2.5 其他训练技巧

     在实验中使用了批标准化，学习率缩放等。

2.6 Test-Time Inference

对于 test-time inference 采用下面三种形式：
1 对于确定性 BinaryConnect 采用二值权值计算
2 使用实数权值计算，二值权值只用于加速训练
3 对于随机二值情况，我们可以将多个随机二值权值系统组合起来得到一个大系统。