[生成对抗网络GAN入门指南](5)WassersteinGAN
本篇blog的内容基于原始论文WassersteinGAN和《生成对抗网络入门指南》第五章。
一、GAN的优化问题
WGAN前作:TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVE ADVERSARIAL NETWORKS
关于GAN的一些问题:训练的不稳定性;理论上,应该先把判别器训练到足够好,但是实际操作发现反而更难去优化生成器。
- 上述论文提出了以下问题:
- 究竟是什么原因导致了判别器越好反而生成器更新越差?
- 为什么训练GAN不稳定?并且很少有理论来支撑GAN?
- 是否有比JS散度类似的代价函数可以使用?
- 有没有方法能避免这些问题?
1. 原始GAN出了什么问题
原始GAN中判别器要最小化下面损失函数
![]()
假定x固定,![]() 和
和![]() 进行求导:
进行求导:
![]()
对于![]() 形式如下:
形式如下:
![]()
然而GAN训练有一个trick,就是别把判别器训练得太好,否则在实验中生成器会完全学不动(loss降不下去)
2. KL和JS散度
先了解一些理论知识。从理论和经验上说,真实数据的分布通常是一个低维度流形(manifold)。流形是数据虽然分布在高维度空间里,但是实际上数据并不具备高维度特性,二世嵌入在高维度的低维度空间里。
现在再回顾之前的生成器,要将低维度的空间Z映射到与真实数据相同的高维度空间上,就是希望我们生成的低维度的manifold能高度逼近真实数据的manifold。
JS散度和KL散度相似,设定![]() ,JS散度公式为:
,JS散度公式为:
把KL公式代入展开:
![]()
可以继续写成
![]()
根据原始GAN定义的判别器loss,我们可以得到最优判别器的形式;而在最优判别器的下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布![]() 与生成分布
与生成分布![]() 之间的JS散度。我们越训练判别器,它就越接近最优,最小化生成器的loss也就会越近似于最小化
之间的JS散度。我们越训练判别器,它就越接近最优,最小化生成器的loss也就会越近似于最小化![]() 和
和![]() 之间的JS散度。
之间的JS散度。
3. 流形:真实数据和生成数据在空间上的关系
如果真实数据和生成数据在空间上完全不相交,可以得到一个完美的判别器划分真实数据和生成数据。实际生活中,生成空间和真实空间完美重合的概率是十分低的,所以大部分情况我们都能找到一个完美的判别器进行划分。也就会导致在网络训练的反向传播中,梯度更新几乎为0,网络难以学到东西。
根据散度公式发现只要生成数据和真实数据没有交集,JS散度始终未常数log2,而他们之间KL散度永远为正无穷。
但是![]() 与
与![]() 不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。比较严谨的答案是:当
不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。比较严谨的答案是:当![]() 与
与![]() 的支撑集(support)是高维空间中的低维流形(manifold)时,
的支撑集(support)是高维空间中的低维流形(manifold)时,![]() 与
与![]() 重叠部分测度(measure)为0的概率为1。
重叠部分测度(measure)为0的概率为1。
不用被奇怪的术语吓得关掉页面,虽然论文给出的是严格的数学表述,但是直观上其实很容易理解。首先简单介绍一下这几个概念:
- 支撑集(support)其实就是函数的非零部分子集,比如ReLU函数的支撑集就是
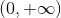 ,一个概率分布的支撑集就是所有概率密度非零部分的集合。
,一个概率分布的支撑集就是所有概率密度非零部分的集合。 - 流形(manifold)是高维空间中曲线、曲面概念的拓广,我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。
- 测度(measure)是高维空间中长度、面积、体积概念的拓广,可以理解为“超体积”。
有了这些理论分析,原始GAN不稳定的原因就彻底清楚了:判别器训练得太好,生成器梯度消失,生成器loss降不下去;判别器训练得不好,生成器梯度不准,四处乱跑。只有判别器训练得不好不坏才行,但是这个火候又很难把握,甚至在同一轮训练的前后不同阶段这个火候都可能不一样,所以GAN才那么难训练。
4. 使用WassersteinGAN
所以有时候尽管生成器表现很好了,与真实数据逼近,但是散度表现依然很差。所以我们更换一种合适的方法计算相似度距离。
1. 这里我们看到GAN很容易发生梯度消失,在训练1/10/25个epoch都很快就迭代掉下了5个数量级。
- 为了防止这个问题,有一个方法是更换不同的梯度函数:
![]()
但是,很多时候还会导致网络更新不稳定的情况。
2. 而且从上图发现曲线噪声也很大。
- 为了减小噪声,是人为地加入随机的噪声
但是,当生成数据与真实数据本身相似度距离较远的话,添加噪声的方案可能就无效了。
提出以上诸多问题后,WassersteinGAN就横空出世了,使用Wasserstein距离计算生成数据和真实数据的差别,代替JS散度和KL散度,从而解决训练不稳定的问题。
二、WGAN的理论研究
1. 距离公式
对于真实数据分布![]() 与生成数据分布
与生成数据分布![]() ,给出以下几种分布距离公式:
,给出以下几种分布距离公式:
总变差距离(total variation distance)和KL散度
然后是JS散度
最后是本篇主角Wasserstein距离(EM距离):
这里可以用一个例子来形容,有两堆泥土,每一堆有 n 个位置,标号从1~n。第一堆泥土的第 i 个位置有 ![]() 克泥土,第二堆泥土的第 i 个位置有
克泥土,第二堆泥土的第 i 个位置有 ![]() 克泥土。小埃可以在第一堆泥土中任意移挪动泥土,具体地从第 i 个位置移动 k 克泥土到第 j 个位置,但是会消耗
克泥土。小埃可以在第一堆泥土中任意移挪动泥土,具体地从第 i 个位置移动 k 克泥土到第 j 个位置,但是会消耗 ![]() 的体力。小埃的最终目的是通过在第一堆中挪动泥土,使得第一堆泥土最终的形态和第二堆相同,也就是
的体力。小埃的最终目的是通过在第一堆中挪动泥土,使得第一堆泥土最终的形态和第二堆相同,也就是![]() , 但是要求所花费的体力最小。
, 但是要求所花费的体力最小。
2. 对距离公式的理解
设想一个二维空间,真实数据分布是X轴为零,Y轴为随机变量的分布,而生成数据的分布是X轴为 ![]() ,Y轴为随机变量的分布,
,Y轴为随机变量的分布,![]() 是生成数据分布的一个变量。根据上述四个公式:
是生成数据分布的一个变量。根据上述四个公式:
也就是说当 ![]() 逼近零时候,只有EM距离在减小,而其他几种距离的公式都是一个固定的值或者无穷大。EM
逼近零时候,只有EM距离在减小,而其他几种距离的公式都是一个固定的值或者无穷大。EM
距离具备一个连续可用的梯度。
3. Wasserstein距离
对于真实数据分布的输入x与生成数据分布的输入x,求满足1-Liposchitz条件的函数f(x)的期望值差值的上确界。
根据1-Liposchitz条件成立,继续改写成
![]()
继续对比GAN和WGAN
三、WGAN的工程实践
看一下WGAN的伪代码:
①分别从真实数据分布和前置随机分布中采样批次。然后进行梯度下降训练判别器:
②结束训练后再从前置随机分布中采样一个批次,使用梯度法训练生成器:
③完整伪代码:
这里和GAN的改动是使用RMSProp方法替代ADAM,这是WGAN作者经过大量实验得出的经验,使用Adam方法会使训练不稳定,而RMSprop可以避免不稳定问题的发生。
具体的差别可以看NG视频的笔记[coursera/ImprovingDL/week2]Optimization algorithms
四、代码
使用keras实现。
1. 导入相关包
from __future__ import print_function, division
from keras.datasets import mnist
from keras.layers import Input, Dense, Reshape, Flatten, Dropout
from keras.layers import BatchNormalization, Activation, ZeroPadding2D
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import UpSampling2D, Conv2D
from keras.models import Sequential, Model
from keras.optimizers import RMSprop
import keras.backend as K
import matplotlib.pyplot as plt
import sys
import numpy as np2. 初始化超参数
- 设置Wasserstein距离作为WGAN损失函数
- 设置判别次数为5,权重裁剪值为0.01
- 将Adam改为RMSProp方法
class WGAN():
def __init__(self):
self.img_rows = 28
self.img_cols = 28
self.channels = 1
self.img_shape = (self.img_rows, self.img_cols, self.channels)
self.latent_dim = 100
# Following parameter and optimizer set as recommended in paper
self.n_critic = 5
self.clip_value = 0.01
optimizer = RMSprop(lr=0.00005)
# Build and compile the critic
self.critic = self.build_critic()
self.critic.compile(loss=self.wasserstein_loss,
optimizer=optimizer,
metrics=['accuracy'])
# Build the generator
self.generator = self.build_generator()
# The generator takes noise as input and generated imgs
z = Input(shape=(100,))
img = self.generator(z)
# For the combined model we will only train the generator
self.critic.trainable = False
# The critic takes generated images as input and determines validity
valid = self.critic(img)
# The combined model (stacked generator and critic)
self.combined = Model(z, valid)
self.combined.compile(loss=self.wasserstein_loss,
optimizer=optimizer,
metrics=['accuracy'])
def wasserstein_loss(self, y_true, y_pred):
return K.mean(y_true * y_pred)3. 构造生成器和DCGAN相同
def build_generator(self):
model = Sequential()
model.add(Dense(128 * 7 * 7, activation="relu", input_dim=self.latent_dim))
model.add(Reshape((7, 7, 128)))
model.add(UpSampling2D())
model.add(Conv2D(128, kernel_size=4, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(UpSampling2D())
model.add(Conv2D(64, kernel_size=4, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(Activation("relu"))
model.add(Conv2D(self.channels, kernel_size=4, padding="same"))
model.add(Activation("tanh"))
model.summary()
noise = Input(shape=(self.latent_dim,))
img = model(noise)
return Model(noise, img)
4. 对判别器修改(最后一层修改)
这里的判别器已经是距离测量的评估者,而非二分类问题的判别器,去除了最后的sigmoid函数。
def build_critic(self):
model = Sequential()
model.add(Conv2D(16, kernel_size=3, strides=2, input_shape=self.img_shape, padding="same"))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(32, kernel_size=3, strides=2, padding="same"))
model.add(ZeroPadding2D(padding=((0,1),(0,1))))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(64, kernel_size=3, strides=2, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Conv2D(128, kernel_size=3, strides=1, padding="same"))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(alpha=0.2))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1))
model.summary()
img = Input(shape=self.img_shape)
validity = model(img)
return Model(img, validity)
5. 训练
训练过程使用权重裁剪使得网络参数保持在一定范围内
def train(self, epochs, batch_size=128, sample_interval=50):
# Load the dataset
(X_train, _), (_, _) = mnist.load_data()
# Rescale -1 to 1
X_train = (X_train.astype(np.float32) - 127.5) / 127.5
X_train = np.expand_dims(X_train, axis=3)
# Adversarial ground truths
valid = -np.ones((batch_size, 1))
fake = np.ones((batch_size, 1))
for epoch in range(epochs):
for _ in range(self.n_critic):
# ---------------------
# Train Discriminator
# ---------------------
# Select a random batch of images
idx = np.random.randint(0, X_train.shape[0], batch_size)
imgs = X_train[idx]
# Sample noise as generator input
noise = np.random.normal(0, 1, (batch_size, self.latent_dim))
# Generate a batch of new images
gen_imgs = self.generator.predict(noise)
# Train the critic
d_loss_real = self.critic.train_on_batch(imgs, valid)
d_loss_fake = self.critic.train_on_batch(gen_imgs, fake)
d_loss = 0.5 * np.add(d_loss_fake, d_loss_real)
# Clip critic weights
for l in self.critic.layers:
weights = l.get_weights()
weights = [np.clip(w, -self.clip_value, self.clip_value) for w in weights]
l.set_weights(weights)
# ---------------------
# Train Generator
# ---------------------
g_loss = self.combined.train_on_batch(noise, valid)
# Plot the progress
print ("%d [D loss: %f] [G loss: %f]" % (epoch, 1 - d_loss[0], 1 - g_loss[0]))
# If at save interval => save generated image samples
if epoch % sample_interval == 0:
self.sample_images(epoch)由于训练速度原因放出前5轮训练结果
0 [D loss: 0.999914] [G loss: 1.000178]50 [D loss: 0.999974] [G loss: 1.000072]100 [D loss: 0.999964] [G loss: 1.000120]150 [D loss: 0.999967] [G loss: 1.000081]
五、实验效果分析
1. 代价函数与生成质量的相关性
①原始论文进行了三种架构的WGAN实验:
- 第一组实验的生成器采用普通的MLP,包含4层,每一层都是512个单元;
- 第二组实验的生成器采用标准的DCGAN,输出层去掉了sigmoid;
- 第三组实验的生成器和判别器都采用MLP;
从第一、二组看出,随着W距离的降低,图像生成质量越来越高;
随着生成器的迭代此处上升,一开始W距离快速下降,慢慢变温度;
最后一组实验不好,随着生成器迭代次数上升,W距离没有下降,但也看到实验效果没有变好,说明理论仍然正确。
②原始GAN采用上述同样配置实验比较
可以看出JS散度变化和生成图像效果没有正相关。且JS散度值趋近常数log2,约等于0.69,最后一组也可以发现两者没有关联。
2. 生成网络的稳定性
①比较WGAN和DCGAN及GAN的生成器效果,可以发现差别不大
②减弱DCGAN的架构,去掉BN,结果WGAN明显更清晰
③使用生成能力较弱的四层ReLU-MLP,WGAN虽然没有之前清晰,但仍然远远超过原始GAN
通过以上实验:WGAN比原始GAN更稳定,而且一旦网络架构出问题,WGAN能一定程度上避免生成图像质量的急速下降。
3. 模式崩溃mode collapse
随着网络的训练,生成器产生的结果是在各个点之间跳跃,但是每次只能产生一个点的数据。
研究人员发表了一些解决模式崩溃的方法,
例如:minibatch:Improved Techniques for Training GANs(NIPs 2016, Ian Goodfellow)
UnrolledGAN:UNROLLED GENERATIVE ADVERSARIAL NETWORKS(ICLR 2017)
但是在WGAN中很少出现模式崩溃
参考令人拍案叫绝的Wasserstein GAN

WassersteinGAN_第1张图片](http://img.e-com-net.com/image/info8/4c173f5a528140adbd566d86f0bc4ac5.jpg)
WassersteinGAN_第2张图片](http://img.e-com-net.com/image/info8/908d62e7fd3241ef9dfaa257d4488bed.jpg)

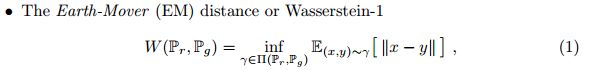
WassersteinGAN_第3张图片](http://img.e-com-net.com/image/info8/e95073a1048c48b990c3b7d1f1845cc7.jpg)
WassersteinGAN_第4张图片](http://img.e-com-net.com/image/info8/def344bb33e9408091d4afe2224f8603.jpg)
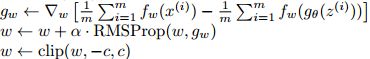
WassersteinGAN_第5张图片](http://img.e-com-net.com/image/info8/abd23c46a52d45efa064e0ad8a5928c4.jpg)
WassersteinGAN_第6张图片](http://img.e-com-net.com/image/info8/6cd84ce9fee9410b867c4d263a696c4f.jpg)
WassersteinGAN_第7张图片](http://img.e-com-net.com/image/info8/7f62c02235144cd2a11a8af7342139e8.jpg)
WassersteinGAN_第8张图片](http://img.e-com-net.com/image/info8/814cbc5da5a049aab8ddfe25b0c1f6b6.jpg)
WassersteinGAN_第9张图片](http://img.e-com-net.com/image/info8/a8696396950d4f1f91c2c6378645a922.jpg)
WassersteinGAN_第10张图片](http://img.e-com-net.com/image/info8/d63407faee104dac931859e62aeaa7e1.jpg)
WassersteinGAN_第11张图片](http://img.e-com-net.com/image/info8/0a1ea026ad9c42b3bdf7a363ec88c1b3.jpg)





