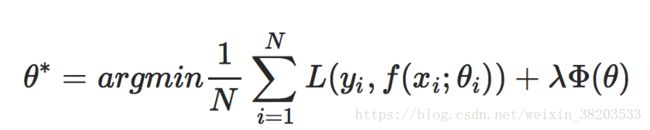图像超分辨率loss以及评估标准的代码实现
图像超分辨率网络loss
1.MSE:MSE表示当前图像X和参考图像Y的均方误差(MeanSquare Error),H、W分别为图像的高度和宽度;n为每像素的比特数,一般取8,即像素灰阶数为256.
代码实现:
mse = tf.reduced_mean(tf.squared_difference(target,output))
2.正则;
一般来说,对分类或者回归模型进行评估时,需要使得模型在训练数据上使得损失函数值最小,即使得经验风险函数最小化,但是如果只考虑经验风险(Empirical risk),容易过拟合,因此还需要考虑模型的泛化能力,一般常用的方法便是在目标函数中加上正则项,由损失项(Loss term)加上正则项(Regularization term)构成结构风险(Structural risk),那么损失函数变为:
上式中的L一长串表示的是一般原问题的的损失函数,加号后面的表示的是由于想到的某些解的特殊性或者说由于条件限制而加入原问题损失函数的一个约束。叫做正则化项(regularizer)或者叫惩罚项(penalty term),它可以是L1,也可以是L2,或者其他的正则函数。L1使用的是绝对值距离,,L2使用的是平方距离。整个式子表示的意思是找到使目标函数最小时的θ值。一般都会在正则化项之前添加一个系数,Python中用表示,这个系数由用户指定。
- L1正则化是指权值向量中各个元素的绝对值之和,通常表示为:L1 loss = ,其导数为
- L2正则化是指权值向量中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为:L2 loss = ,其导数为 ;
添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
- L1正则化当惩罚参数充分大时可以把某些待估的回归系数精确地收缩到0,即可以产生稀疏权值矩阵,可以用于特征选择。稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
- L2正则化可以防止模型过拟合(overfitting);
L1_loss函数
代码实现:
loss= tf.reduce_mean(tf.losses.absolute_difference(target,output))
L2_loss函数
tf.nn.l2_loss(t, name=None)该函数的作用是利用 L2 范数来计算张量的误差值
但是没有开方并且只取 L2 范数的值的一半,具体如下:
output = sum(t ** 2) / 2
输入参数:t: 一个Tensor。数据类型:float32,float64,int64,int32,uint8,int16,int8,complex64,qint8,quint8,qint32。
虽然一般情况下,数据维度是二维的。但是,数据维度可以取任意维度。
name: 操作名称。
输出参数:Tensor ,数据类型和 t 相同,是一个标量。
代码实现1:
loss= tf.reduce_sum(tf.nn.l2_loss(tf.substract(target,output)))
for w in weights:
loss += tf.nn.l2_loss(w)*1e-4
代码实现2:(给RGB设置不同的权重)
def loss(inferences, ground_truthes, weights_decay=0, name='loss'):
with tf.name_scope(name):
slice_begin = (int(ground_truthes.get_shape()[1]) - int(inferences.get_shape()[1])) // 2
slice_end = int(inferences.get_shape()[1]) + slice_begin
delta = inferences - ground_truthes[:, slice_begin: slice_end, slice_begin: slice_end, :]
delta *= [[[[0.11448, 0.58661, 0.29891]]]] # weights of B, G and R
l2_loss = tf.pow(delta, 2)
mse_loss = tf.reduce_mean(tf.reduce_sum(l2_loss, axis=[1, 2, 3]))
if weights_decay > 0:
weights = tf.get_collection('weights')
reg_loss = weights_decay * tf.reduce_sum(tf.pack([tf.nn.l2_loss(i) for i in weights]), name='regularization_loss')
return mse_loss + reg_loss
else:
return mse_loss
评估标准
1.PSNR(PeakSignal to Noise Ratio)峰值信噪比:单位是dB,数值越大表示失真越小。
PSNR是最普遍和使用最为广泛的一种图像客观评价指标,然而它是基于对应像素点间的误差,并未考虑到人眼的视觉特性。因为人眼对空间频率较低的对比差异敏感度较高,对亮度对比差异的敏感度较色度高,人眼对一个区域的感知结果会受到其周围邻近区域的影响,因而经常出现评价结果与人的主观感觉不一致的情况。
代码实现:psnr = tf.constant(255**2,dtype = tf.float32)/mse
psnr = tf.constant(10,dtype=tf.float32)*tf.log(psnr)/tf.log(tf.constant(10,dtype=tf.log(psnr.dtype)))