『为金融数据打标签』「2. 元标签方法」
本文有 6161 字,20 图表截屏
建议阅读 32 分钟
0
引言
本文是 AFML 系列的第五篇
金融数据类型
从 Tick 到 Bar
基于事件采样
三隔栏方法
元标签方法
要构建一个模型来决定是否买卖某个资产,我们需要
确定头寸方向(side)
当价格涨或正收益到一定程度,做多
当价格跌或负收益到一定程度,做空
其他情况下,什么都不用做
确定头寸大小(size),甚至包括不下单(size = 0)
在〖三隔栏方法〗一贴里,我们已经解决了第一个问题,即根据止损止盈来给数据打标签。本帖则关注第二个问题,即如果下单,该下多少。
1
基础常识
在〖三隔栏方法〗一贴里,我们给数据打的标签分三类(假设头寸是做多):
y = 1,当上水平隔栏先被触及
y = -1,当下水平隔栏先被触及
y = 0,当垂直隔栏先被触及
但如果头寸是做空,那么给数据打的标签则变成
y = 1,当下水平隔栏先被触及
y = -1,当上水平隔栏先被触及
y = 0,当垂直隔栏先被触及
总结:如果同时考虑做多和做空,数据标签可表述成
当 y = 1 时,止盈隔栏先被触及
当 y = -1 时,止损隔栏先被触及
当 y = 0 时,垂直隔栏先被触及
上面问题的分类是一个多分类问题,在交易中,我们只想分两类:
交易(无论做多和做空)
不交易
因此上述三类标签可等价转换成下面两类标签:
交易 - 当 y = 1 或 -1,做多或做空
不交易 - 当 y = 0,做毛
或
交易 - 对应 ymeta = 1
不交易 - 对应 ymeta = 0
其中 ymeta 是元标签(meta label)。
在交易时,下面哪种预测错误的情况更严重?
情况 1 - 预测要交易(做多或做空)但是错了(做多时价格跌或做空是价格涨),这种情况称为假正类(false positive)
情况 2 - 预测不交易但是错了(价格有变动),这种情况称为假负类(false negative)
情况 1 你犯错会亏钱,情况 2 你犯错只是失去赚钱的机会,情况 1 的假正类更严重。
相信你已经被绕晕了,我们先从熟悉的 MNIST 手写数字分类问题下手,来介绍和元标签相关的各种概念。弄懂基本概念后再回到金融资产数据打标签的问题。
2
元标签 - MNIST 分类
以下代码是在 sklearn 0.22 版本下运行的,就是为了使用 plot_roc_curve 这个方便的函数。该函数可以用一行代码画出 ROC-AUC 图,详情见〖盘一盘 Python 特别篇 - Sklearn 0.22〗一帖。
import sklearn
print(sklearn.__version__)
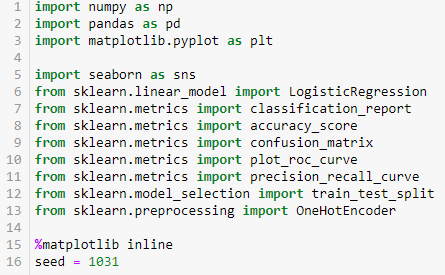
0.22首先引入必要的包,代码如下:
2.1
预处理数据
下载 MNIST 数据,并按 80:20 划分训练集和测试集。
看看从 0 到 9 的十类数字标签的个数,分布还蛮平均。
sns.countplot(y_test);
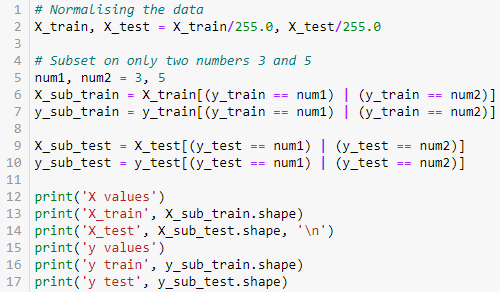
首先将 0-255 的像素值标准化到 0-1 之间。其次我们考虑一个二分类问题,只识别数字 3 和 5,因此从原数据集中选取子集。
X values
X_train (10707, 784)
X_test (2747, 784)
y values
y train (10707,)
y test (2747,)假设我们把数字 3 定义成正类,数字 5 定义负类,用 1 和 0 代表正类和负类(由于该问题是二分类,因此不需要做独热编码)。
2.2
初级模型
初级模型我们选择对率回归模型 LogisticRegression。
为了让模型一开始表现不是那么好(想通过元标签的方法改进模型),我们将 max_iter 设置为 3,即优化器迭代 3 次就停,可想而知结果不会太好。但这就是我们希望看到的模型初始表现。
model = LogisticRegression( max_iter=3 )
model.fit( X_sub_train, y_sub_train )
训练集表现
看看模型在训练集上的准确率(accuracy),才 89% 多。
prediction = model.predict(X_sub_train)
print(prediction)
print(y_sub_train)
print(accuracy_score(y_sub_train, prediction))
[0 1 1 ... 1 0 0]
[0 1 1 ... 1 1 0]
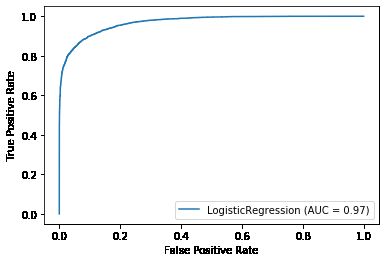
0.8920332492761744画出模型在训练集上的 ROC 图。
plot_roc_curve( model, X_sub_train, y_sub_train );
打印出模型在训练集上的分类报告和混淆矩阵。
print( classification_report(y_sub_train, prediction) )
print( confusion_matrix(y_sub_train, prediction))
先看一个「混淆矩阵」的知识点。
混淆矩阵
在分类任务中,模型预测和标签总不是完全匹配,而混淆矩阵 (confusion matrix) 就是记录模型表现的 N×N 表格 (其中 N 为类别的数量),通常一个轴列出真实类别,另一个轴列出预测类别。
对于二分类问题,可将样例根据其真实类别与模型预测类别的组合划分为真正类 (true positive, TP),真负类 (true negative, TN),假正类 (false positive, FP) 和假负类 (false negative, FN)。
预测类别的真假来描述“正类负类”,预测为真 = 正类,预测为假 = 负类。
真实类别和预测类别的同异来描述“真假”,相同= 真,不同 = 假。
真正类 = 预测类别为真且和真实类别相同,真负类 = 预测类别为假且和真实类别相同。
假正类 = 预测类别为真但和真实类别不同,假负类 = 预测类别为假和真实类别不同。
以二分类任务 (识别一个数字是 3 还是 5) 为例 N = 2 的混淆矩阵的一般形式和具体例子如下:
真负类:预测是 5 (负类),而且分类正确。
假正类:预测是 3 (正类),但是分类错误。
假负类:预测是 5 (负类),但是分类错误。
真正类:预测是 3 (正类),而且分类正确。
正规化 (normalized) 的混淆矩阵显示的不是 TP, FN, FP, TN 的个数,而是它们的百分比,转换过程如下
TP→TP/(TP+FN)
FN→FN/(TP+FN)
FP→FP/(FP+TN)
TN→TN/(FP+TN)
在 Sklearn 中混淆矩阵的 TP, FN, FP 和 TN 的摆放位置和我们习惯理解的不一样,如下图。
在做分类定义正类负类时,我们最关注的点是要预测好正类,即预测完正类希望错误越少越好,即假正类(false positive)越小越好。从上图看 FP 有 785 个,模型还需改进啊。
测试集表现
看看模型在测试集上的准确率(accuracy)89.04%,比训练集上略小一点点。
prediction_test = model.predict(X_sub_test)
print(prediction_test)
print(y_sub_test)
print(accuracy_score(y_sub_test, prediction_test))
[1 1 1 ... 1 1 1]
[1 1 1 ... 1 1 0]
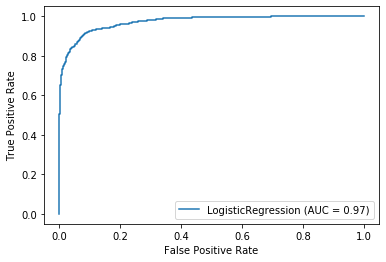
0.8904259191845649画出模型在测试集上的 ROC 图,和在训练集上的图相似。
plot_roc_curve( model, X_sub_test, y_sub_test );
打印出模型在测试集上的分类报告和混淆矩阵。
print( classification_report(y_sub_test, prediction_test) )
print( confusion_matrix(y_sub_test, prediction_test) )
比较模型在训练集和测试集的分类报告,我们发现查准(precision)、查全(recall)和 F-得分(f1-score)各项指标相当,因此模型没有过拟合,但模型表现还可以再进一步提升吗?
2.3
高查全率的初级模型
在两分类模型中,首先计算出预测样本为正类和负类的概率,然后选取 0.5 作为阈值,概率大于 0.5 的样本作为正类,概率小于 0.5 的样本作为负类。
现在我们希望模型有高查全率,即最好不要漏掉正类,即更容易得能预测正类,即阈值要调低。极端情况阈值为 0, 那么所有概率都大于 0,所有样本都预测为正类。
首先用 predict_proba() 函数获取模型的预测正类负的概率,该模型有两列,第一列是预测负类的概率,第二列是预测正类的概率,我们需要第二列,因此在下面代码中,用 [:,1] 获取第二列作为 y_score。
y_score = model.predict_proba(X_sub_train)[:,1]
小一点阈值才能提高查全率,这里我们先设置它为 0.2,然后将所有概率大于 0.2 对应样本对划分成正类。
thres = 0.2
prediction_high_recall = (y_score > thres).astype(int)
对于这个高查全率的初级模型,打印出其在训练集上的分类报告和混淆矩阵。
print( classification_report(y_sub_train, prediction_high_recall) )
print( confusion_matrix(y_sub_train, prediction_high_recall) )
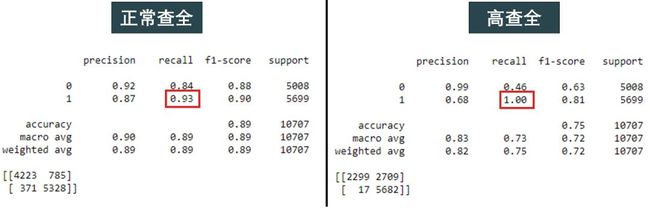
从图中第三行看出查全率接近于 1,但查准率下降的不少。
比较正常查全(阈值为 0.5)和高查全(阈值为 0.2)的分类报告展示如下:
除了查全率,其他指标都大幅下降。但这不是终点,这一切都在为次级模型做准备。
2.4
次级模型
核心内容来了,如何构建元特征(meta feature)和元标签(meta label)?
元特征:将高查全率的模型预测和原特征合并。
元标签:将高查全率的模型预测和原标签求交集。
元特征没什么好讲的,只是将初级模型的预测当做额外特征。但元标签背后的逻辑就厉害了,它目的是来验证初级模型预测的正类到底是真还是假。
代码如下:
meta_features = np.hstack((prediction_high_recall.reshape(-1,1),
X_sub_train))
meta_labels = prediction_high_recall & y_sub_train
为了比较使用元标签对相同模型带来的提升,次级模型还是用 LogisticRegression,实际上次级模型可以用其他模型的。
meta_model = LogisticRegression()
meta_model.fit( meta_features, meta_labels )
最终预测是元模型的预测和高查全模型的预测的交集。
meta_prediction = meta_model.predict(meta_features)
final_prediction = meta_prediction & prediction_high_recall
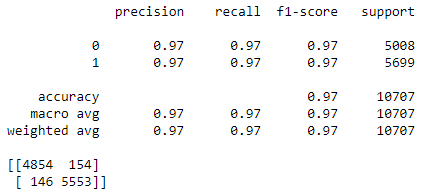
打印出次级模型在训练集上的分类报告和混淆矩阵。
print( classification_report(y_sub_train, final_prediction) )
print( confusion_matrix(y_sub_train, final_prediction) )
下图对比「不用元标签」和「用元标签」,发现模型的各项指标大幅度提升。
2.5
2.1
小结
将前面做的事情整理到函数 meta_label_report,它有五个参数,前两个是训练好的初级模型和次级模型,接着是特征 X 和标签 y(它们可以是训练集和测试集),最后一个是阈值,控制初级模型的查全率,阈值越小查全率越高。
完整代码如下,写的应该很清晰了。
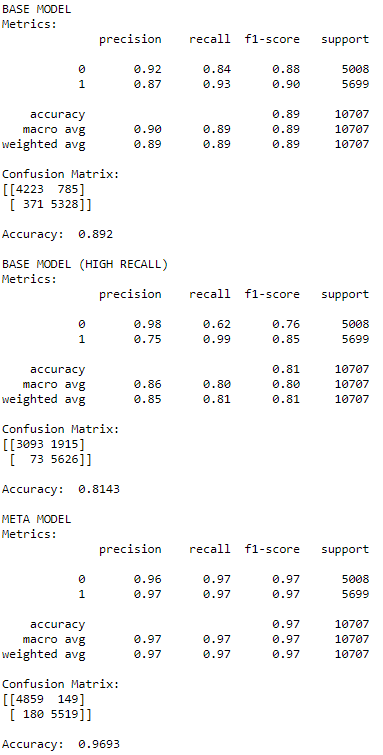
在训练集上打印报告,结果很合理。
meta_label_report( model, meta_model, X_sub_train, y_sub_train, 0.3 )
次级模型下的各项指标都是最高,而且 FP 的个数减少了很多。
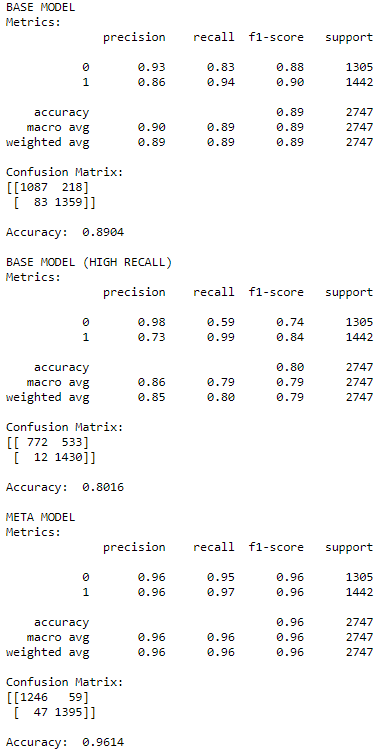
接着在测试集上打印报告,结果很合理。
meta_label_report( model, meta_model, X_sub_test, y_sub_test, 0.3 )
次级模型下的各项指标都是最高,而且 FP 的个数减少了很多。
3
元标签 - 金融资产数据
在给金融资产数据打标签的整个流程分为两步:
确定基础标签 ybase:用〖三隔栏方法〗一贴介绍的方法
当 ybase = 1 时,止盈隔栏先被触及
当 ybase = -1 时,止损隔栏先被触及
当 ybase = 0 时,垂直隔栏先被触及
确定元标签 ymeta:即是否按着头寸方向交易
当 ybase = 1 并且 rtrue > c 而触发止盈时,设置ymeta = 1;当 ybase = -1 并且 rtrue < -c 而触发止损时,设置 ymeta = 1
其他情况统统设置 ymeta = 0。
来个一图胜千言。
类比 MNIST 的例子,我们首先建立一个初级模型(记着要尽量提高查准率)来预测头寸方向,但在增加真正类的情况下也增加了假正类,这是交易中最不原因看到的(预测要交易但是错了已经损失真金白银)。
随后我们对模型预测的正例使用元标签,并建立次级模型来提高查准率。该模型的主要目的是从已经挑选出的机会中再一次筛选投资标的。
当次级模型是机器学习相关模型时,就有意思了。因此机器学习中的分类器不仅能返回类别,而且可以返回类别对应的概率,概率越大,预测该类别的信心越足,那么在交易时不就可以增加头寸大小了么?
元标签方法可以看成是一个次级模型,其美妙之处在于,你可以把元标签方法可加载任何初级模型上,不管它是
机器学习模型
计量经济学公式
基本面分析
技术分析
人主观看法
它有以下几点优势:
提升了模型的可解读性。先通过简单模型(如基本面或者人的看法)来确定头寸方向,随后再使用复杂模型(如机器学习模型)
限制了过拟合。在元标签之后,复杂模型将只决定头寸大小而非方向
头寸方向和头寸大小的分解允许我们先简后繁。例如我们可以使用复杂模型分别对多头和空头进行专门训练确定头寸大小
4
总结
通过 MNIST 的例子可看出元标签可以有效帮助我们提升查准率、查全率和 F-得分。
在金融数据打标签的应用上,元标签是指在第一个模型已经确定头寸方向的情况下,希望通过第二个模型来确定头寸大小。
头寸大小 = f(预测概率)
而预测该类的概率是任何机器学习的分类模型的副产品,在 scikit-learn 中,用 predict_proba() 可以得到预测概率。
p_pred = model.predict_proba(X_test)
假设我们用随机森林预测出概率为 p,在实际交易中,一种决策可以是
p < 55%,不要做多
p ∈ [55%, 60%],用 50% 资金做多
p > 60%,用 100% 资金做多
当初级模型用主观看法,而次级模型用客观数据,这种投资方法称为
量化基本面投资(Quantitative Fundamental, Quantamental)。
量化基本面投资其实是一种对基本面投资和量化投资的融合,是将计算机算法与人类的分析结合起来的一种 1+1>2 的新型投资方式。
使用基本面模型挑选标的并确定头寸方向,使用元标签方法确定标签。
使用机器学习模型在元标签进行训练,得出概率可转化成头寸大小。
Keras 的大神创作者 François Chollet 曾经评价过浅度学习(shallow)和深度学习(deep learning)相结合的方法在 AI 界非常成功。
… very successful in practice… blending deep learning with shallow learning
也许在量投界,浅度模型(初级)加上深度模型(次级)也会非常成功。
Stay Tuned!
![]()