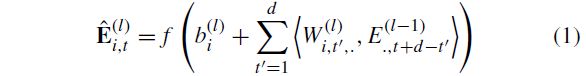【Paper】LSTM-FCN: LSTM Fully Convolutional Networks for Time Series Classification

论文年份：2017
论文被引：211(04/26/20)
论文原文：点击此处
论文源码：点击此处

---

---

LSTM Fully Convolutional Networks for Time Series Classification

Fully convolutional neural networks (FCNs) have been shown to achieve the state-of-theart performance on the task of classifying time series sequences. We propose the augmentation of fully convolutional networks with long short term memory recurrent neural network (LSTM RNN) sub-modules for time series classification. Our proposed models significantly enhance the performance of fully convolutional networks with a nominal increase in model size and require minimal preprocessing of the data set. The proposed long short term memory fully convolutional network (LSTM-FCN) achieves the state-of-theart performance compared with others. We also explore the usage of attention mechanism to improve time series classification with the attention long short term memory fully convolutional network (ALSTM-FCN). The attention mechanism allows one to visualize the decision process of the LSTM cell. Furthermore, we propose refinement as a method to enhance the performance of trained models. An overall analysis of the performance of our model is provided and compared with other techniques.

INDEX TERMS Convolutional neural network, long short term memory recurrent neural network, time series classification.

全卷积神经网络（FCN）已显示在对时间序列进行分类的任务中实现了最先进的性能。我们建议使用长期短期记忆递归神经网络（LSTM RNN）子模块增强全卷积网络，以进行时间序列分类。我们提出的模型以模型尺寸的名义上的增加显着增强了全卷积网络的性能，并且需要对数据集进行最少的预处理。拟议的长期短期记忆全卷积网络（LSTM-FCN）与其他网络相比，可实现最新的性能。我们还探索了注意力机制的使用，以通过注意力长期短期记忆完全卷积网络（ALSTM-FCN）改善时间序列分类。注意机制允许人们可视化LSTM单元的决策过程。此外，我们提出了改进方法，以增强训练模型的性能。提供了对模型性能的全面分析，并将其与其他技术进行了比较。

关键词：卷积神经网络，长期短期记忆递归神经网络，时间序列分类。

---

I. INTRODUCTION

Over the past decade, there has been an increased interest in time series classification. Time series data is ubiquitous [1], existing in weather readings [2], financial recordings [3], industrialobservations[4],andpsychologicalsignals[5],[6]. Several approaches, including feature-based [7], ensembles [8]–[10], and deep learning [11], [12], have been utilized to classify time series. Deep learning has been successfully utilized in various applications that require time series data, especially in control systems [13], [14]. In this paper, two deep learning models to classify time series datasets are proposed, both of which outperform existing state-of-the-art models and do not require heavy preprocessing.

在过去的十年中，人们对时间序列分类越来越感兴趣。时间序列数据无处不在[1]，存在于天气读数[2]，财务记录[3]，工业观测[4]和心理信号[5]，[6]中。几种方法，包括基于特征的[7]，集合[8]-[10]和深度学习[11]，[12]，已被用于对时间序列进行分类。深度学习已成功用于需要时间序列数据的各种应用程序中，尤其是在控制系统中[13]，[14]。在本文中，提出了两种用于对时间序列数据集进行分类的深度学习模型，它们均优于现有的最新模型，并且不需要大量的预处理。

A plethora of research has been done using feature-based approaches or methods to extract a set of features that represent time series patterns. Bag-of-Words (BoW) [15], Bagof-features (TSBF) [16], Bag-of-SFA-Symbols (BOSS) [17], BOSSVS [18], and Word ExtrAction for time Series cLassification (WEASEL) [19] have obtained promising results in the field. Bag-of-words quantizes the extracted features and feeds the BoW into a classifier. TSBF extracts multiple subsequences of random local information, which a supervised learner condenses into a cookbook used to predict time series labels. BOSS introduces a combination of a distance based classifier and histograms. The histograms represent substructures of a time series that are created using a symbolic Fourier approximation. BOSSVS extends this method by proposing a vector space model to reduce time complexity while maintaining performance. WEASEL converts time series into feature vectors using a sliding window. Machine learning algorithms utilize these feature vectors to detect and classify the time series. All these classifiers require heavy feature extraction and feature engineering. Using multiple of these feature-based algorithms as an ensemble algorithm yields better results.

已经使用基于特征的方法或方法进行了大量研究，以提取代表时间序列模式的一组特征。时间序列分类（WEASEL）的词袋（BoW）[15]，词袋特征（TSBF）[16]，SFA符号袋（BOSS）[17]，BOSSVS [18]和Word ExtrAction [19]在该领域取得了可喜的成果。词袋对提取的特征进行量化，并将BoW馈入分类器。 TSBF提取随机局部信息的多个子序列，有监督的学习者将这些子序列浓缩为用于预测时间序列标签的菜谱。 BOSS引入了基于距离的分类器和直方图的组合。直方图表示使用符号傅立叶逼近创建的时间序列的子结构。 BOSSVS通过提出向量空间模型来扩展此方法，以减少时间复杂度并保持性能。 WEASEL使用滑动窗口将时间序列转换为特征向量。机器学习算法利用这些特征向量来检测和分类时间序列。所有这些分类器都需要繁重的特征提取和特征工程。将这些基于特征的算法中的多个算法用作集成算法可产生更好的结果。

Ensemble algorithms also yield state-of-the-art performance with time series classification problems. Three of the most successful ensemble algorithms that integrate various features of a time series are Proportional Elastic Ensemble (PROP) [20], a model that integrates 11 time series classifiers using a weighted ensemble method, shapelet ensemble (SE) [8], a model that applies a heterogeneous ensemble onto transformed shapelets, and a flat collective of transform based ensembles (COTE) [8], a model that fuses 35 various classifiers into a single classifier.

集成算法还可以产生具有时间序列分类问题的最新性能。三种最成功的集成时间序列特征的集成算法是比例弹性集成（PROP）[20]，该模型使用加权集成方法集成了11个时间序列分类器，即小波集成（SE）[8]。该模型将异构集合应用于已变形的Shapelet，以及一个基于变换的集成的平面集合（COTE）[8]，该模型将35个不同的分类器融合为一个分类器。

Recently, deep neural networks have been employed for time series classification tasks. Multi-scale convolutional neural network (MCNN) [12], fully convolutional network (FCN) [11], and residual network (ResNet) [11] are deep learning approaches that take advantage of convolutional neural networks (CNN) for end-to-end classification of univariate time series. MCNN uses down-sampling, skip sampling and sliding window to preprocess the data. The performance of the MCNN classifier is highly dependent on the preprocessing applied to the dataset and the tuning of a largesetofhyperparametersofthatmodel.Ontheotherhand, FCN and ResNet do not require any heavy preprocessing on the data or feature engineering.

最近，深度神经网络已被用于时间序列分类任务。多尺度卷积神经网络（MCNN）[12]，全卷积网络（FCN）[11]和残差网络（ResNet）[11]是利用卷积神经网络（CNN）进行端到端的深度学习方法变量时间序列的末端分类。 MCNN使用下采样，跳过采样和滑动窗口对数据进行预处理。 MCNN分类器的性能高度依赖于应用于数据集的预处理以及对该模型的大量超参数的调整。另一方面，FCN和ResNet不需要对数据或要素工程进行任何繁重的预处理。

In this paper, we improve the performance of FCN by augmenting the FCN module with either a Long Short Term Recurrent Neural Network (LSTM RNN) sub-module, called LSTM-FCN, or a LSTM RNN with attention, called ALSTM-FCN. In addition, the Attention LSTM can also be used detect regions of the input sequence that contribute to the class label through the context vector of the Attention LSTM cells. Results indicate the new proposed models, LSTM-FCN and ALSTM-FCN, dramatically improve performance on the University of California Riverside (UCR) Benchmark datasets [21]. LSTM-FCN and ALSTM-FCN produce better results than several state-of-the-art algorithms on a majority of the UCR Benchmark datasets.

在本文中，我们通过使用称为LSTM-FCN的长期短期递归神经网络（LSTM RNN）子模块或称为ALSTM-FCN的LSTM RNN扩展FCN模块来提高FCN的性能。另外，Attention LSTM也可以用于检测输入序列的区域，这些区域通过Attention LSTM单元的上下文向量对类别标签有贡献。结果表明，新提出的模型LSTM-FCN和ALSTM-FCN大大提高了University of California Riverside（UCR）基准数据集的性能[21]。与大多数UCR Benchmark数据集上的几种最新算法相比，LSTM-FCN和ALSTM-FCN产生更好的结果。

This paper proposes two deep learning models for endto-end time series classification. The proposed models do not require heavy preprocessing on the data or feature engineering. Both the models are tested on all 85 UCR time series benchmarks and outperform most of the state-of-theart models. The remainder of the paper is organized as follows. Section II reviews the background work. Section III presents the architecture of the proposed models. Section IV analyzes and discusses the experiments performed. Finally, conclusions are drawn in Section V.

本文为端到端时间序列分类提出了两种深度学习模型。提出的模型不需要对数据或特征工程进行大量预处理。两种模型均在所有85个UCR时间序列基准上进行了测试，并优于大多数最新模型。在本文的其余部分安排如下。第二节回顾了背景工作。第三节介绍了提出的模型的体系结构。第四节分析并讨论了进行的实验。最后，在第五节中得出结论。

---

II. BACKGROUND WORKS

A. TEMPORAL CONVOLUTIONS

The input to a Temporal Convolutional Network is generally a time series signal. As stated in Lea et al. [22], let $X_t\in {\mathbb{R}}^{F_0}$ be the input feature vector of length $F_0$ for time step $t$ for $0<t\le T$. Note that the time $T$ may vary for each sequence, and we denote the number of time steps in each layer as $T_l$. The true action label for each frame is given by $y_t\in 1,...,C$, where $C$ is the number of classes.

时间卷积网络的输入通常是时间序列信号。 如Lea等人所述。 [22]，令 $X_t\in {\mathbb{R}}^{F_0}$ 为长度为 $F_0$ 时间步长为 $t$ 的输入特征向量，其中 $0<t\le T$。 注意，时间 $T$ 对于每个序列可以变化，并且我们将每个层中的时间步数表示为 $T_1$。 每帧的真实动作标签由 $y_t\in 1，...，C$ 给出，其中 $C$是类数。

Consider $L$ convolutional layers. We apply a set of $1D$ filters on each of these layers that capture how the input signals evolve over the course of an action. According to Lea et al. [22], the filters for each layer are parameterized by tensor $W^{(l)}\in {\mathbb{R}}^{F_l\times d\times F_{l-1}}$ and biases $b^{(l)}\in R^{F_l}$, where $l\in 1,...,L$ is the layer index and $d$ is the filter duration. For the $l-th$ layer, the $i-th$ component of the (unnormalized) activation ${\hat{E}}_t^{(l)}\in {\mathbb{R}}^{F_l}$ is a function of the incoming (normalized) activation matrix $E^{(l-1)}\in R^{F_{l-1}\times T_{l-1}}$ from the previous layer

for each time t where f (·) is a Rectified Linear Unit.

考虑 $L$ 卷积层。我们在这些层中的每一层应用一组1D滤波器，捕捉输入信号在动作过程中的变化。根据Lea等人的说法。[22]用张量 $W^{(l)}\in {\mathbb{R}}^{F_l\times d\times F_{l-1}}$ 和偏置 $b^{(l)}\in R^{F_l}$ 对每一层的滤波器进行参数化，其中 $l\in 1,...,L$ 是层索引，$d$ 是过滤持续时间。对于第 $l$ 层，非标准化的激活函数 ${\hat{E}}_t^{(l)}\in {\mathbb{R}}^{F_l}$ 的第 $i$ 个分量是来自前一层的传入（标准化的）时间 $t$ 时的激活函数矩阵 $E^{(l-1)}\in R^{F_{l-1}\times T_{l-1}}$ ，其中 $f(\cdot )$ 是校正线性单元（ReLU）。

We use Temporal Convolutional Networks as a feature extraction module in a Fully Convolutional Network (FCN) branch. A basic convolution block consists of a convolution layer, followed by batch normalization [23], followed by an activation function, which can be either a Rectified Linear Unit or a Parametric Rectified Linear Unit [24].

在全卷积网络（FCN）分支中，我们使用时间卷积网络作为特征提取模块。基本卷积块包括卷积层，接着是批量标准化[23]，接着是激活函数，激活函数可以是校正线性单元或参数校正线性单元[24]。

B. RECURRENT NEURAL NETWORKS

Recurrent Neural Networks, often shortened to RNNs, are a class of neural networks which exhibit temporal behaviour due to directed connections between units of an individual layer. As reported by Pascanu et al. [25], recurrent neural networks maintain a hidden vectorh, which is updated at time step t as follows:

递归神经网络，通常简称为RNNs，是一类由于单个层单元之间的有向连接而表现出时间行为的神经网络。如Pascanu等人所述。[25]，递归神经网络保持一个隐藏向量，在时间步骤t更新如下：

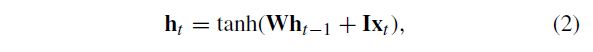
tanh is the hyperbolic tangent function, W is the recurrent weight matrix and I is a projection matrix. The hidden state h is used to make a prediction

tanh是双曲正切函数，W是递推权重矩阵，I是投影矩阵。隐藏状态h用于进行预测

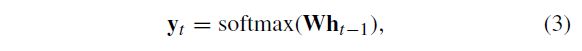
softmax provides a normalized probability distribution over the possible classes, σ is the logistic sigmoid function and Wis a weight matrix. By usinghas the input to another RNN, we can stack RNNs, creating deeper architectures

softmax提供了可能类上的规范化概率分布，σ是logistic sigmoid函数，W是权重矩阵。通过使用另一个RNN的输入，可以堆叠RNN，创建更深层的体系结构

---

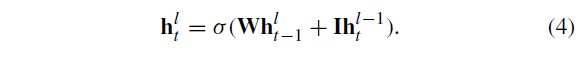
C. LONG SHORT-TERM MEMORY RNNs

Long short-term memory recurrent neural networks are an improvement over the general recurrent neural networks, which possess a vanishing gradient problem. As stated in Hochreiter and Schmidhuber [26], LSTM RNNs address the vanishing gradient problem commonly found in ordinary recurrent neural networks by incorporating gating functions into their state dynamics. At each time step, an LSTM maintains a hidden vector h and a memory vector m responsible for controlling state updates and outputs. More concretely, Graves et al. [27] define the computation at time step t as follows :

长短期记忆递归神经网络是对一般递归神经网络的改进，它具有消失梯度问题。如Hochreiter和Schmidhuber[26]所述，LSTM RNN通过将选通函数纳入其状态动力学，解决了普通递归神经网络中常见的消失梯度问题。在每个时间步骤，LSTM维护隐藏向量h和负责控制状态更新和输出的存储器向量m。更具体地说，格雷夫斯等人。[27]定义时间步骤t的计算如下：

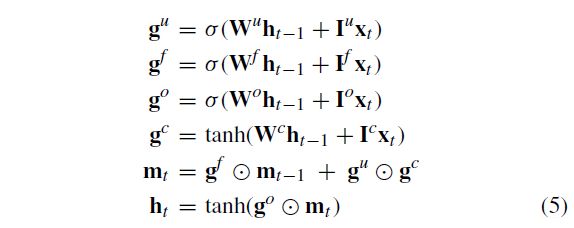
where $\sigma$ is the logistic sigmoid function, $⨀$ represents elementwise multiplication, $W_u,W_f,W_o,W_c$ are recurrent weight matrices and $I_u,I_f,I_o,I_c$ are projection matrices.

其中 $\sigma$ 是logistic sigmoid函数，$⨀$表示元素乘法，$W_u，W_f，W_o，W_c$是递归权重矩阵，$I_u，I_f，I_o，I_c$是投影矩阵。

While LSTMs possess the ability to learn temporal dependencies in sequences, they have difficulty with long term dependencies in long sequences. The attention mechanism proposed by Bahdanau et al. [28] can help the LSTM RNN learn these dependencies.

虽然LSTMs能够学习序列中的时间依赖项，但在长序列中很难学习长时间依赖项。Bahdanau等人提出的注意机制。[28]可以帮助LSTM RNN学习这些依赖关系。

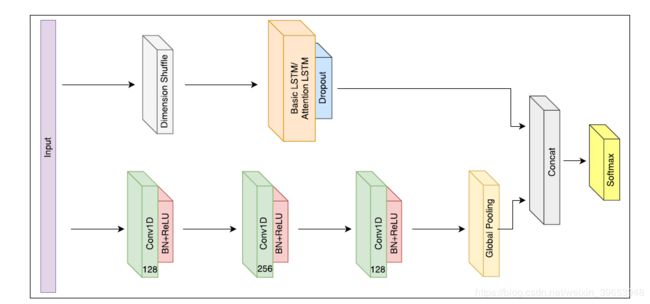
FIGURE 1. The LSTM-FCN architecture. LSTM cells can be replaced by Attention LSTM cells to construct the ALSTM-FCN architecture.

---

D. ATTENTION MECHANISM

The attention mechanism is a technique often used in neural translation of text, where a context vector $C$ is conditioned on the target sequence $y$. As discussed in Bahdanau et al. [28], the context vector $c_i$ depends on a sequence of annotations $(h_1,...,h_{T_x})$ to which an encoder maps the input sequence. Each annotation hicontains information about the whole input sequence with a strong focus on the parts surrounding the $i-th$ word of the input sequence.The context vector $c_i$ is then computed as a weighted sum of these annotations $h_i$:

注意机制是文本神经翻译中经常使用的一种技术，其中上下文向量 $C$ 是以目标序列 $y$ 为条件的，如Bahdanau等人所讨论的。[28]，上下文向量 $c_i$ 取决于编码器将输入序列映射到的注释序列 $(h_1,...,h_{T_x})$。每个注释 $h_i$ 都包含有关整个输入序列的信息，并重点关注输入序列的第 $i$ 个单词周围的部分。

然后，将上下文向量 $c_i$ 计算为这些注释的加权和 $h_i$：

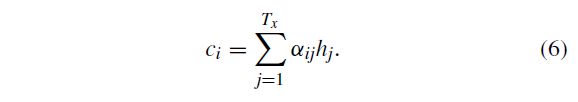
where $e_{ij}=a(s_{i-1},h_j)$ is an alignment model, which scores how well the input around position j and the output at position i match. The score is based on the RNN hidden state $s_{i\hat{a}{\acute{L}}^{\prime }1}$ and the j-th annotation $h_j$ of the input sentence.

其中 $e_{ij}=a(s_{i-1}，h_j)$ 是一个对齐模型，它对位置j周围的输入与位置 $i$ 处的输出的匹配程度进行评分。 得分基于RNN隐藏状态 $s_{i\hat{a}{\acute{L}}^{\prime }1}$ 和输入语句的第$j$ 个注释 $h_j$。

Bahdanau et al. [28] parametrize the alignment model $a$ as a feedforward neural network which is jointly trained with all the other components of the model. The alignment model directly computes a soft alignment, which allows the gradient of the cost function to be backpropagated.

Bahdanau等人。[28]将对准模型 $a$ 参数化为一个前馈神经网络，它与模型的所有其他组成部分联合训练。对齐模型直接计算软对齐，允许成本函数的梯度反向传播。

---

III. LSTM FULLY CONVOLUTIONAL NETWORK

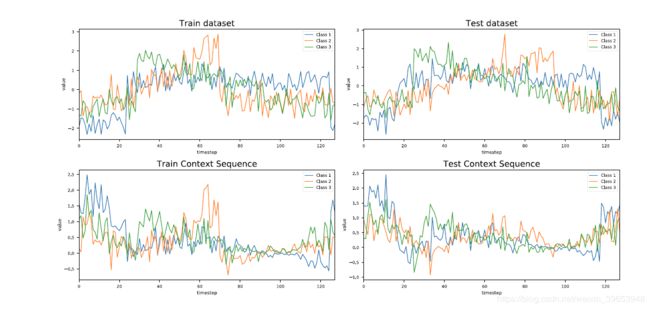
FIGURE 2. Visualization of context vector on CBF dataset.

A. NETWORK ARCHITECTURE

Temporal convolutions have proven to be an effective learning model for time series classification problems [11]. Fully Convolutional Networks, comprised of temporal convolutions, are typically used as feature extractors. Global average pooling [29] is used to reduce the number of parameters in the model prior to classification. In the proposed models, the fully convolutional block is augmented by an LSTM block followed by dropout [30], as shown in Figure 1.

时间卷积被证明是时间序列分类问题的有效学习模型[11]。由时间卷积组成的全卷积网络通常用作特征提取器。全局平均池化[29]用于在分类之前减少模型中的参数数量。在所提出的模型中，全卷积块由LSTM块加dropout[30]组成，如图1所示。

The fully convolutional block consists of three stacked temporal convolutional blocks with filter sizes of 128, 256, and 128 respectively. Each convolutional block is identical to the convolution block in the CNN architecture proposed by Wang et al. [11]. Each block consists of a temporal convolutional layer, which is accompanied by batch normalization [23] (momentum of 0.99, epsilon of 0.001) and followed by a ReLU activation function. Finally, global average pooling is applied after the final convolution block.

全卷积块由三个堆叠的时间卷积块组成，它们的滤波器大小分别为128、256和128。每个卷积块与Wang等人提出的CNN架构中的卷积块相同。 [11]。每个块由一个时间卷积层组成，使用批量归一化[23]（动量为0.99，ε为0.001），然后是ReLU激活函数。最后，在最后的卷积块之后应用全局平均池化。

Simultaneously, the time series input is conveyed into a dimension shuffle layer (explained more in Section III-B). The transformed time series from the dimension shuffle is then passed into the LSTM block. The LSTM block, comprising of either a general LSTM layer or an Attention LSTM layer, is followed by a dropout. The output of the global poolinglayerandtheLSTMblockisconcatenatedandpassed onto a softmax classification layer.

同时，时间序列输入被传送到维度混洗层（dimension shuffle layer）（在第III-B节中有更多说明）。然后将来自维度混洗的变换后的时间序列传递到LSTM块中。由常规LSTM层或Attention LSTM层组成的LSTM块后面是一个辍学部分。全局池层和LSTM块的输出被串联并传递到softmax分类层。

---

B. NETWORK INPUT

The fully convolutional block and LSTM block perceive the same time series input in two different views. The fully convolutional block views the time series as a univariate time series with multiple time steps. If there is a time series of length N, the fully convolutional block will receive the data in N time steps.

全卷积块和LSTM块在两个不同的视图中感知相同的时间序列输入。全卷积块将时间序列视为具有多个时间步长的单变量时间序列。如果存在一个长度为N的时间序列，则全卷积块将以N个时间步长接收数据。

In contrast, the LSTM block in the proposed architecture receives the input time series as a multivariate time series with a single time step. This is accomplished by the dimension shuffle layer, which transposes the temporal dimension of the time series. A univariate time series of length N,after transformation, will be viewed as a multivariate time series (having N variables) with a single time step. Without the dimension shuffle, the performance of the LSTM block is significantly reduced due to the rapid overfitting of small short-sequence UCR datasets and a failure to learn long term dependencies in the larger long-sequence UCR datasets.

相反，所提出的体系结构中的LSTM块将输入时间序列作为具有单个时间步长的多元时间序列来接收。这是通过维度混洗层实现的，该层对时间序列的时间维度进行转置。长度为N的单变量时间序列，转换后，将被视为具有单个时间步长的多元时间序列（具有N个变量）。如果不进行尺寸调整，由于小的短序列UCR数据集的快速过拟合以及无法学习较大的长序列UCR数据集中的长期依存关系，LSTM块的性能将大大降低。

In addition, dimension shuffle improves the efficiency of this model by requiring an order of magnitude less time to train. When a dataset of N time steps and M variables use a LSTM without dimension shuffling, the LSTM will require N time steps to process a batch of M variables. In contrast, applying the dimension shuffle to the input will allow the LSTM model to process a batch of N variables in M time steps. This suggests that as long as the number of variables M is significantly smaller than the number of time steps N, dimension shuffle will greatly improve the speed of training. As each of the UCR datasets is univariate, the LSTM component of this model will require only 1 time step to process a batch of N variables.

另外，维度混洗通过减少所需的训练时间来提高此模型的效率。当N个时间步长和M个变量的数据集使用不带维数改组的LSTM时，LSTM将需要N个时间步长来处理一批M个变量。相比之下，将尺寸改组应用于输入将允许LSTM模型以M个时间步长处理一批N个变量。这表明，只要变量数M显着小于时间步长N，维数改组将极大地提高训练速度。由于每个UCR数据集都是单变量的，因此该模型的LSTM组件仅需要1个时间步即可处理一批N变量。

To illustrate this, a total of 18 hours is required on a single GTX 1080 Ti to train an LSTM-FCN for each of the 85 UCR datasets, and 19 hours for ALSTM-FCN.Without the dimension shuffle, it would take more than 100 hours to train the respective models on all 85 UCR datasets.

为了说明这一点，单个GTX 1080 Ti总共需要18个小时来训练85个UCR数据集中的LSTM-FCN，而ALSTM-FCN则需要19个小时。如果不进行维变换，则在所有85个UCR数据集上训练各自的模型将花费100多个小时。

---

C. REFINEMENT OF MODELS

Transfer learning is a technique wherein the knowledge gained from training a model on a dataset can be reused when training the model on another dataset, such that the domain of the new dataset has some similarity with the prior domain [31]. Similarly, we propose refinement, which can be can be described as transfer learning on the same dataset.

迁移学习是一种技术，其中当在另一个数据集上训练模型时，可以重复使用从在一个数据集上训练模型所获得的知识，从而使新数据集的域与先前域具有某些相似性[31]。同样，我们提出了改进，可以将其描述为对同一数据集的转移学习。

The training procedure can thus be split into two distinct phases. In the initial phase, the optimal hyperparameters for the model are selected for a given dataset. The model is then trained on the given dataset with these hyperparameter settings. In the second step, we apply refinement to this initial model.

训练过程因此可以分为两个不同的阶段。在初始阶段，为给定数据集选择模型的最佳超参数。然后使用这些超参数设置在给定的数据集上训练模型。在第二步中，我们对初始模型进行优化。

The procedure of transfer learning is iterated over in the refinement phase, using the original dataset. Each repetition is initialized using the model weight of the previous iteration. At each iteration the learning rate is halved. Furthermore, the batch size is halved once every alternate iteration. This is done until the initial learning rate is 1e−4 and batch size is 32. The procedure is repeated K times, where K is an arbitrary constant, generally set as 5.

迁移学习的过程在优化阶段使用原始数据集进行迭代。使用上一次迭代的模型权重初始化每个重复。在每次迭代中，学习率减半。此外，每个备用迭代将批次大小减半。一直执行到初始学习率为1e-4且批大小为32为止。此过程重复K次，其中K为任意常数，通常设置为5。

Refinement is a procedure which successively attempts to improve the performance of a pre-trained model. As discussed by Huang et al. [32], multiple local minima lie along the optimization path of a model. Once a model has converged to some local minima during its initial training phase, it can be re-trained using a larger learning rate to escape the previous minima and hopefully land upon a better local minima.

细化是连续尝试提高a的性能的过程。预训练模型。如Huang等人所述。 [32]，沿着模型的优化路径存在多个局部最小值。一旦模型在初始训练阶段收敛到某个局部最小值，就可以使用更高的学习率对其进行重新训练，以逃避先前的最小值，并希望落入一个更好的局部最小值。

Re-training while simultaneously reducing the learning rate and batch size allows for a more refined search to the best local optima.

重新训练，同时降低学习率和批量大小，可以进行更精细的搜索以达到最佳的局部最优。

---

IV. EXPERIMENTS

The proposed models have been tested on all 85 UCR time series datasets [21]. The FCN block was kept constant throughout all experiments. The optimal number of LSTM cells was found by hyperparameter search over a range of 8 cells to 128 cells. The number of training epochs was generally kept constant at 2000 epochs, but was increased for datasets where the algorithm required a longer time to converge. Initial batch size of 128 was used, and halved for each successive iteration of the refinement algorithm. A high dropout rate of 80% was used after the LSTM or Attention LSTM layer to combat overfitting. Class imbalance was handled via a class weighing scheme inspired by King and Zeng [33]. All models were trained using the Keras [34] library with the TensorFlow [35] backend.

所提出的模型已经在所有85个UCR时间序列数据集上进行了测试[21]。在所有实验中，FCN块均保持恒定。通过超参数搜索在8个单元至128个单元的范围内找到了LSTM单元的最佳数量。训练epoch的数量通常保持在2000个epoch，但对于算法需要较长时间收敛的数据集，则增加了。使用的初始批处理大小为128，对于优化算法的每个连续迭代，将其减半。在LSTM或Attention LSTM层之后使用了80％的高辍学率来防止过度拟合。分类失衡是由King和Zeng [33]提出的班级称重方案处理的。使用带有TensorFlow [35]后端的Keras [34]库对所有模型进行了训练。

All models were trained via the Adam optimizer [36], with an initial learning rate of 1e−3 and a final learning rate of 1e−4. All convolution kernels were initialized with the initialization proposed by He et al. [37]. The learning rate was reduced by a factor of $\frac{1}{\sqrt[3]{2}}$ every 100 epochs of no improvement in the validation score, until the final learning rate was reached. No additional preprocessing was done on the UCR datasets as they have close to zero mean and unit variance. All models were refined. Scores stated in Table 1 refer to the scores obtained by models prior to and after refinement.1

所有模型都通过Adam优化器[36]进行了训练，初始学习率为1e-3，最终学习率为1e-4。所有卷积内核都使用He等人提出的初始化方法进行了初始化。 [37]。如果验证准确率在连续100个epochs内没有改善，则学习率降低 $\frac{1}{\sqrt[3]{2}}$ ，直到达到最终学习率。由于UCR数据集的均值和单位方差接近零，因此无需进行其他预处理。所有模型都经过精制。表1中列出的分数是指模型在精炼之前和之后所获得的分数。

---

A. EVALUATION METRICS

In this paper, the proposed model was evaluated using accuracy, rank based statistics, and the mean per class error as stated by Wang et al. [11]. The rank-based evaluations used are the arithmetic rank, geometric rank, and the Wilcoxon signed rank test. The arithmetic rank is the arithmetic mean of the rank of dataset. The geometric rank is the geometric mean of the rank of each dataset. The Wilcoxson signed rank test is used to compare the median rank of the proposed model and the existing state-of-the-art models. The null hypothesis and alternative hypothesis are as follows:

在本文中，如Wang等人所述，使用准确性，基于等级的统计数据和每类均值误差对提出的模型进行了评估。 [11]。使用的基于等级的评估是算术等级，几何等级和Wilcoxon有符号等级检验。算术等级是数据集等级的算术平均值。几何等级是每个数据集的等级的几何平均值。 Wilcoxson带符号秩检验用于比较提议的模型和现有的最新模型的中位数。零假设和替代假设如下：

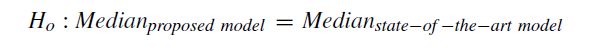
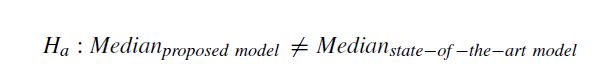
平均每类错误（MPCE）定义为每类错误（PCE）的算术平均值，

---

B. RESULTS

TABLE 2. Wilcoxon signed rank test comparison of each model.

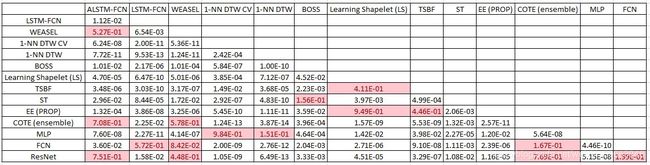
TABLE 3. Summary of advantages of the proposed models.

Figure 2 is an example of the visual representation of the Attention LSTM cell on the ‘‘CBF’’ dataset. The points in the figure where the sequences are ‘‘squeezed’’ together are points at which all the classes have the same weight. These are the points in the time series at which the Attention LSTM can correctly identify the class. This is further supported by visual inspection ofthe actual time series. The squeezepoints are points where each of the classes can be distinguished from each other, as shown in Figure 2.

图2是“ CBF”数据集上Attention LSTM单元的直观表示示例。图中顺序被“挤压”在一起的点是所有类别具有相同权重的点。这些是时间序列中Attention LSTM可以正确识别类别的点。通过目视检查实际时间序列进一步支持了这一点。挤压点是可以区分每个类的点，如图2所示。

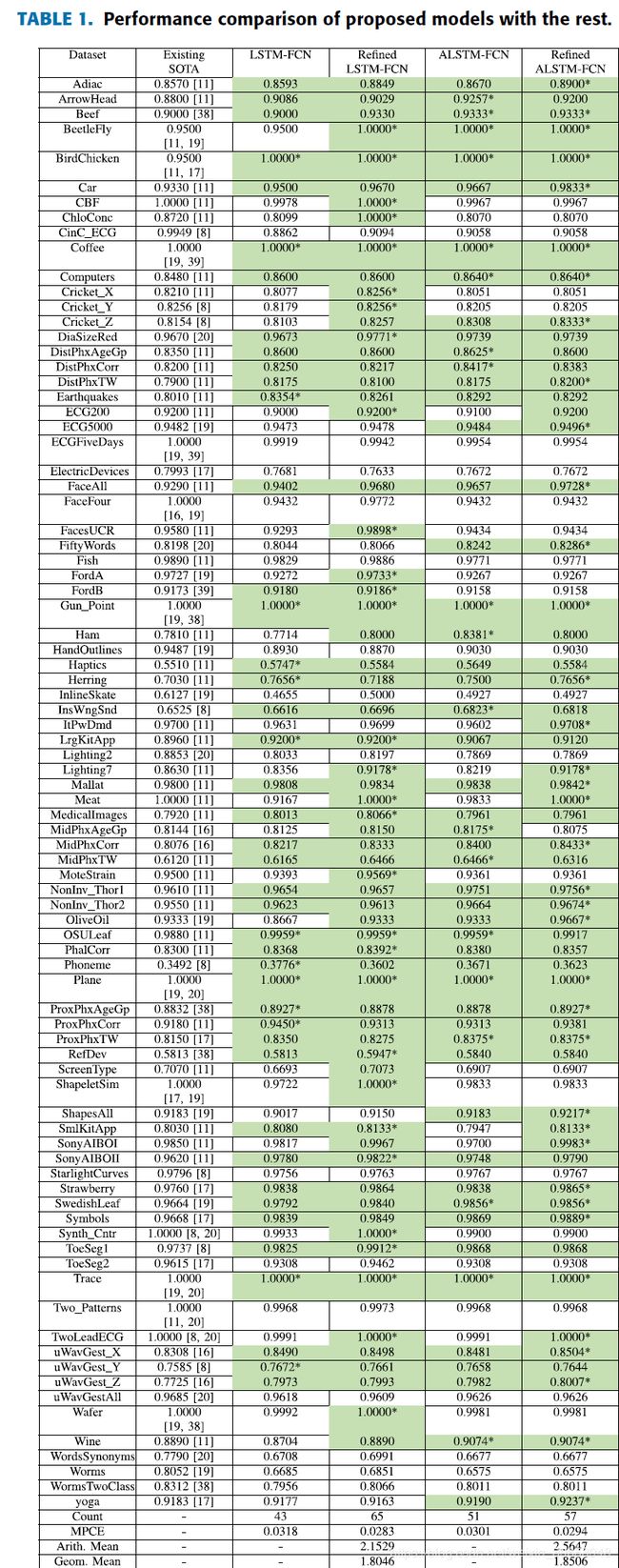
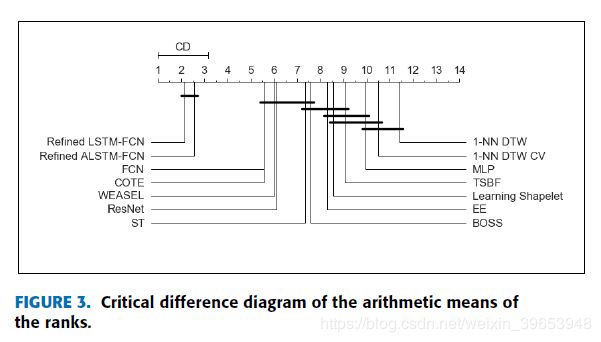
The performance of the proposed models on the UCR datasets are summarized in Table1. The colored cells are cells that outperform the state-of-the-art model for that dataset. Both proposed models, the ALSTM-FCN model and the LSTM-FCN model, with both phases, without refinement (Phase 1) and with refinement (Phase 2), outperforms the state-of-the-art models in at least 43 datasets. The average arithmetic rank in Figure 3 indicates the superiority of our proposed models over the existing state-of-the-art models. This is further validated using the Wilcoxon signed rank test, where the p-value of each of the proposed models are less than 0.05 when compared to existing state-of-the-art models, Table 2.

表1总结了建议模型在UCR数据集上的性能。有色单元格是优于该数据集的最新模型的单元格。两种建议的模型，ALSTM-FCN模型和LSTM-FCN模型，无论是在两个阶段，都没有精炼（阶段1）还是经过精炼（阶段2），在至少43个数据集中都超过了最新模型。图3中的平均算术等级表明我们提出的模型优于现有的最新模型。使用Wilcoxon符号秩检验进一步验证了这一点，与现有的最新模型相比，每个提议模型的p值均小于0.05（表2）。

The Wilcoxon Signed Test also provides evidence that refinement maintains or improves the overall accuracy on each of the proposed models. The MPCE of the LSTM-FCN and ALSTM-FCN models was found to reduce by 0.0035 and 0.0007 respectively when refinement was applied.Refinement improves the accuracy of the LSTM-FCN models on a greater number of datasets as compared to the ALSTM-FCN models. We postulate that this discrepancy is due to the fact that the LSTM-FCN model contains fewer total parameters than the ALSTM-FCN model. This indicates a lower rate of overfitting on the UCR datasets. As a consequence, refinement is more effective on the LSTM-FCN models for the UCR datasets.

Wilcoxon签名测试还提供了证据，表明改进可以保持或提高每个提议模型的总体准确性。当进行细化时，LSTM-FCN和ALSTM-FCN模型的MPCE分别降低了0.0035和0.0007。与ALSTM-FCN模型相比，精化提高了LSTM-FCN模型在更多数据集上的准确性。我们假定这种差异是由于LSTM-FCN模型包含的总参数少于ALSTM-FCN模型的事实。这表明UCR数据集的过拟合率较低。因此，在针对UCR数据集的LSTM-FCN模型上，优化更为有效。

A significant drawback of refinement is that it requires more training time due to the added computational complexity of re-training the model using smaller batch sizes. The disadvantages of refinement are mitigated when using the ALSTM-FCN within Phase 1. At the end of Phase 1, the ALSTM-FCN model outperforms the Phase 1 LSTMFCN model. One of the major advantage of using the Attention LSTM cell is it provides a visual representation of the attention vector. The Attention LSTM also benefits from refinement, but the effect is less significant as compared to the general LSTM model. A summary of the performance of each model type on certain characteristics is provided on Table 3.

改进的一个显着缺点是，由于使用较小的批处理量重新训练模型会增加计算复杂性，因此需要更多的训练时间。在阶段1中使用ALSTM-FCN时，可以减轻优化的缺点。在阶段1结束时，ALSTM-FCN模型的性能优于阶段1的LSTMFCN模型。使用Attention LSTM单元的主要优点之一是它提供了注意力向量的可视表示。 Attention LSTM也可以从改进中受益，但与普通LSTM模型相比，效果不那么明显。表3提供了每种模型在某些特性上的性能摘要。

---

V. CONCLUSION & FUTURE WORK

With the proposed models, we achieve a notable improvement on the current state-of-the-art for time series classification using deep neural networks. Our baseline models, with and without refinement, are trainable end-to-end with nominal preprocessing and are able to achieve significantly improved performance. LSTM-FCNs are able to augment FCN models, appreciably increasing their performance with a nominal increase in the number of parameters. ALSTM-FCNs enable one to visually inspect the decision process of the LSTM RNN and provide a strong baseline on their own. Refinement can be applied as a general procedure to a model to further elevate its performance. The strong increase in performance in comparison to the FCN models shows that LSTM RNNs can beneficially supplement the performance of FCN modules for time series classification. An overall analysis of the performance of our model is provided and compared to other techniques.

借助提出的模型，我们在使用深度神经网络进行时间序列分类的当前最新技术方面取得了显着改进。我们的基准模型，无论是否经过改进，都可以通过名义上的预处理进行端到端的培训，并且能够显着提高性能。 LSTM-FCN能够扩充FCN模型，并通过名义上增加参数数量来显着提高其性能。 ALSTM-FCN使人们能够直观地检查LSTM RNN的决策过程，并自行提供强大的基准。细化可以作为一般过程应用于模型，以进一步提高其性能。与FCN模型相比，性能的强劲增长表明LSTM RNN可以有益地补充FCN模块的时间序列分类性能。提供了对模型性能的整体分析，并将其与其他技术进行了比较。

Due to the generality of the input to this model, it has wide ranging applicability on several sequence modelling tasks such as text analysis, music recognition and voice detection. Furthermore, due to its small size and efficiency, it can be easily deployed to real time systems or embedded systems. Additional research is to be done on understanding why the Attention LSTM cell is unsuccessful in matching the performance of the general LSTM cell on some of the datasets.

由于此模型输入的通用性，因此它在多种序列建模任务（例如文本分析，音乐识别和语音检测）上具有广泛的适用性。此外，由于其体积小，效率高，因此可以轻松地部署到实时系统或嵌入式系统中。在理解为什么Attention LSTM单元无法在某些数据集上匹配常规LSTM单元的性能时，还需要进行其他研究。

---