支持向量机SVM----学习笔记二(代码实践一线性分类)
本篇主要记录如何使用sklearn去实现线性SVM,使用的是鸢尾花数据集,在对SVM进行分类前,和KNN一样我们首先,要对数据进行标准化处理,这是因为SVM寻找的是使margin最大的区间中间的那根线,而我们衡量margin的方式是数据点之间的距离,如果数据点在不同维度上量纲不同的话,那对于距离的估计就是有问题的。
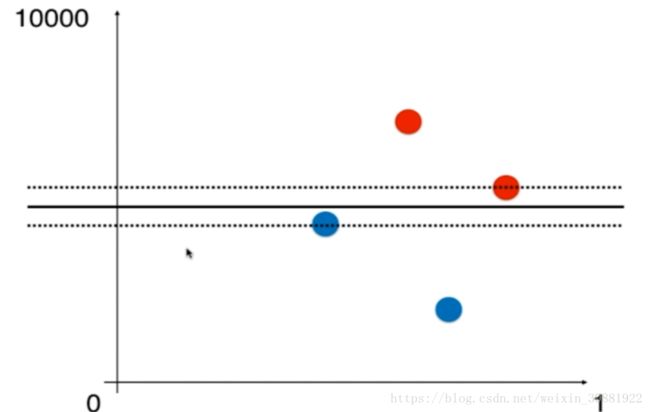
例如在下图中,横轴范围在0-1,纵轴范围却在0-10000,对应的决策边界只能这么划分,虽然看上去尺度很短,但是纵轴是从0-10000,纵轴上很短的距离都代表一个很大的数。
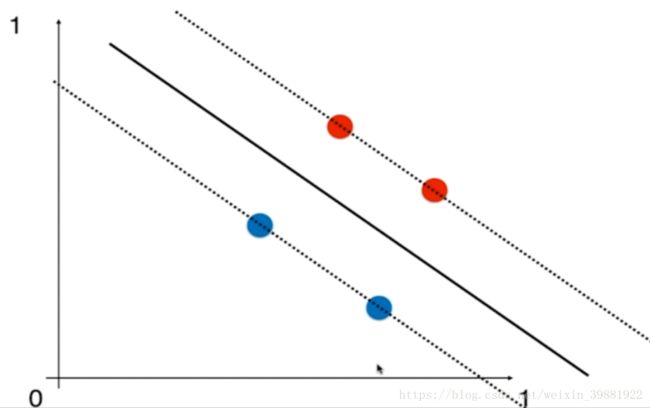
但如果横纵项范围都是在0-1范围里,此时决策边界变为如下所示:
总之,对于SVM来说,如果特征在不同的维度上数据尺度不同的话,将会非常严重影响SVM得到的决策边界,为了避免这种情况的出现,再使用SVM之前,应对数据进行标准化处理。
Scikit-learn中的SVM
1.准备数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris=datasets.load_iris()
X=iris.data
print(X)
Y=iris.target
print(Y)
#处理二分类问题,所以只针对Y=0,1的行,然后从这些行中取X的前两列
x=X[Y<2,:2]
y=Y[Y<2]
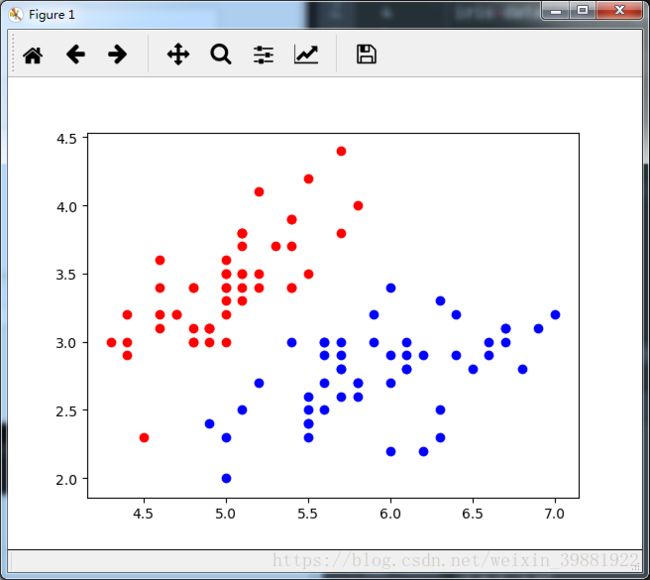
#target=0的点标红,target=1的点标蓝,点的横坐标为data的第一列,点的纵坐标为data的第二列
plt.scatter(x[y==0,0],x[y==0,1],color='red')
plt.scatter(x[y==1,0],x[y==1,1],color='blue')
plt.show()X:
[[ 5.1 3.5 1.4 0.2]
[ 4.9 3. 1.4 0.2]
[ 4.7 3.2 1.3 0.2]
[ 4.6 3.1 1.5 0.2]
[ 5. 3.6 1.4 0.2]
[ 5.4 3.9 1.7 0.4]
[ 4.6 3.4 1.4 0.3]
...
[ 6.5 3. 5.2 2. ]
[ 6.2 3.4 5.4 2.3]
[ 5.9 3. 5.1 1.8]]
Y:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
x:
[[ 5.1 3.5]
[ 4.9 3. ]
[ 4.7 3.2]
[ 4.6 3.1]
[ 5. 3.6]
[ 5.4 3.9]
...
[ 6.2 2.9]
[ 5.1 2.5]
[ 5.7 2.8]]
y:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
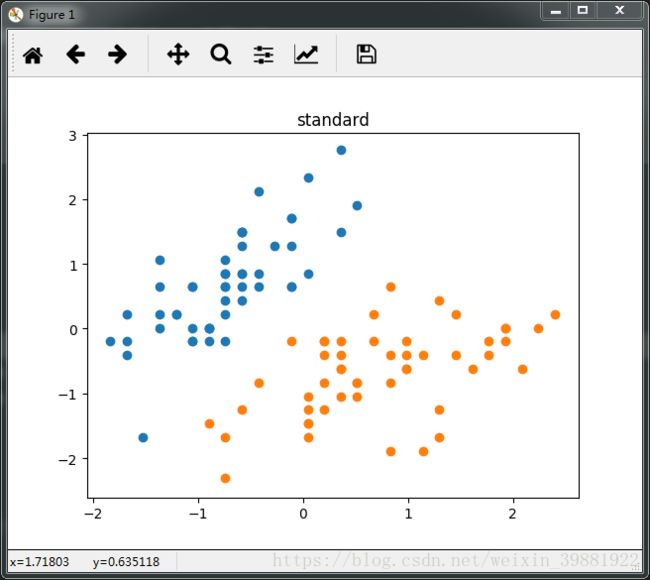
2.对数据进行标准化
#在用SVM进行分类前,要对数据进行标准化
from sklearn.preprocessing import StandardScaler
#实例化一个标准化对象
standardScaler=StandardScaler()
standardScaler.fit(x)
#完成了对数据x的标准化
x_standard=standardScaler.transform(x)3.使用SVM算法对此数据进行分类
当C很大时,趋向硬间隔
#引入线性SVM SVC:Support vector classifier
from sklearn.svm import LinearSVC
#C越大,允许的容错空间越小,越偏向与hard margin(线性可分)
svc1=LinearSVC(C=1e9)
svc1.fit(x_standard,y)
print(svc1)
def plot_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
)
x_new=np.c_[x0.ravel(),x1.ravel()]
#对横坐标axis[2]到axis[3]x0,纵坐标axis[0]到axis[1]x1进行组合,组合成n行两列的数据点,对这些数据点进行预测
y_predict=model.predict(x_new).reshape(x0.shape)
#引入ListedColormap用于生成非渐变的颜色映射
from matplotlib.colors import ListedColormap
# 自定义colormap
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
#contourf(x, y, z)对等高线间的填充区域进行填充(使用不同的颜色)x和y为两个等长一维数组,第三个参数z为二维数组(表示平面点xi,yi映射的函数值)。
plt.contourf(x0,x1,y_predict,linewidth=5,cmap=custom_cmap)
plot_decision_boundary(svc1,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
plt.title('svc1:C=1e9')
plt.show()
#特征有两个,打印这两个特征的系数
print(svc1.coef_)
#直线截距
print(svc1.intercept_)
LinearSVC(C=1000000000.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)[[ 4.03236788 -2.49296525]]
[ 0.9536577]
直线可以表示为:4.03236788*x0-2.49296525x1+0.9536577=0
当C较小时,趋向软间隔,容错空间越大
#C越小,允许的容错空间越大,越偏向soft margin(线性不可分)
svc2=LinearSVC(C=0.001)
svc2.fit(x_standard,y)
print(svc2)
LinearSVC(C=0.001, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
plot_decision_boundary(svc2,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
plt.title('svc2:C=0.001')
plt.show()
[[ 0.11775399 -0.1101242 ]]
[ 5.02216183e-09]4.将C=1e9和C=0.01两种情况下SVM的margin画出来
#添加margin边界的绘制
def plot_svc_decision_boundary(model,axis):
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_predict=model.predict(x_new).reshape(x0.shape)
from matplotlib.colors import ListedColormap
# 自定义colormap
custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,y_predict,linewidth=5,cmap=custom_cmap)
#sklearn中的svm可以直接处理多分类问题,但是我们这里只处理二分类问题,只有一根直线,所以取二维数组中的第1个元素
w=model.coef_[0]
b=model.intercept_[0]
'''
w0*x0+w1*x1+b=0-->决策边界方程x1=-w0*x0/w1-b/w1
w0*x0+w1*x1+b=-1-->margin下边缘边缘方程x1=-w0*x0/w1-b/w1-1/w1
w0*x0+w1*x1+b=1-->margin上边缘方程x1=-w0*x0/w1-b/w1+1/w1
'''
plot_x=np.linspace(axis[0],axis[1],200)
down_y = -w[0] * plot_x / w[1] - b / w[1] - 1/w[1]
up_y=-w[0]*plot_x/w[1]-b/w[1]+1/w[1]
#此时求出的up_y和down_y有可能已经超出了传进来的axis边界值,需要进行一下过滤,通过bool数组来索引合格的数据点
up_index=(up_y>=axis[2])&(up_y<=axis[3])
down_index = (down_y >= axis[2]) & (down_y <= axis[3])
plt.plot(plot_x[up_index],up_y[up_index],color='black')
plt.plot(plot_x[down_index],down_y[down_index],color='black')
plot_svc_decision_boundary(svc1,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
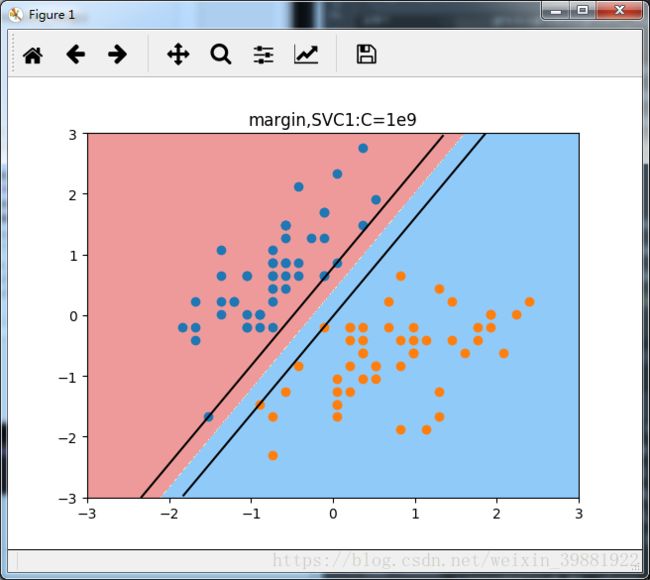
plt.title('margin,SVC1:C=1e9')
plt.show()
plot_svc_decision_boundary(svc2,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
plt.title('margin,SVC2:C=0.01')
plt.show()通过SVC1中的图,可以清晰的看出来,margin上边界有三个数据点落在直线上,下边界有两个数据点落在直线上,这些点就是支持向量,这种情况下相当于是硬间隔,在margin中间,没有任何数据点,既保证正确的将数据点分成了两类,且让两类数据点离决策边界最近的数据点又尽可能的远。
在SVC2中,给了很大的容错空间,所以在图中,margin中包含了许多数据点,且错分了一个蓝色的数据点。
补充:
LinearSVC中,multi_class='ovr'代表二分类问题,多分类问题设置成multi_class='ovo';penalty='l2':采用L2范式进行正则化