最短路径--dijkstra算法、弗洛伊德(Floyd)算法(带路径输出)
####最短路径
求最短路径重要性不言而喻,下面直接分析两个算法。
分类:
1:从某个源点到其余个点的最短路径
迪杰斯特拉(Dijkstra)算法
2:每一对之间的最短路径
弗洛伊德(Floyd)算法
####一:存储结构
邻接矩阵(这里不再重复讲了,请参考):
https://blog.csdn.net/weixin_39956356/article/details/80470091
相关代码:
//邻接矩阵
#define INT__MAX 65000 //最大值65535,表示两顶点没有联系
#define MAX_VERTEX_NUM 20 //最多顶点数
typedef char VertexType;
typedef int EdgeType;
//顶点信息
typedef struct ArcCell {
EdgeType wight;
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //二维数组
//弧的信息
typedef struct MGraph {
VertexType vexs[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum, arcnum; //图的当前顶点数和弧数
}MGraph;
####创建有向图
注意一下(有向图):G.arcs[i][j].wight = w;
相关代码:
//建立无向图的邻接矩阵
void CreatMGraph(MGraph &G)
{
for (int i = 0; i < G.vexnum; i++) {
printf("Please enter %d data:", i + 1);
scanf(" %c", &G.vexs[i]); //输入顶点值
}
for (int i = 0; i####二:迪杰斯特拉(Dijkstra)算法,带输出路径
自己将这个算法分成两部分:
一:最短路径长度
二:最短路径
####首先,我们先看最短路径长度问题
1:这里需要引入一个辅助数组Dij[],每次遍历一遍数组得到本次数组中最小值及所在位置。

2:找到最小值,并入S集
![]()
3:更新新的路径值
判断条件:还没有并入S集,且有更小的路径值
if (!isGetShortestPath[w] && (min + G.arcs[minIndex][w].wight < Dij[w]))
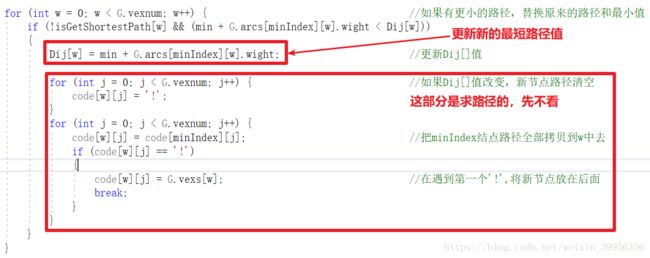
####其次,最短路径
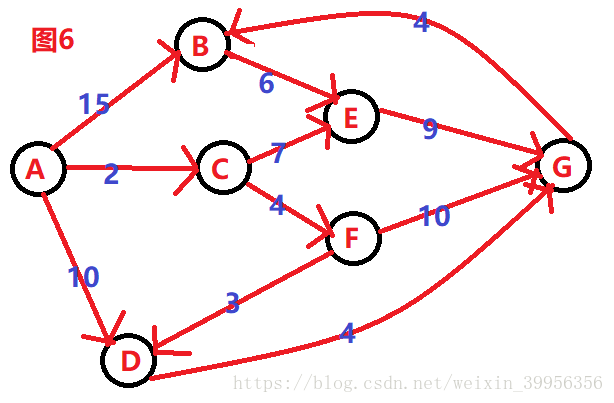
我拿一个图来讲解,整个流程。不防举A->E。它的最短路径是A->C->E,我们分析下
1:这里需要引入一个辅助Code数组code[][],记录走过的最短路径,初始值不防赋值为’!’。

2:清空E结点该行
3:把C结点路径拷贝到E中
4:在第一个 ! ,添加尾结点E
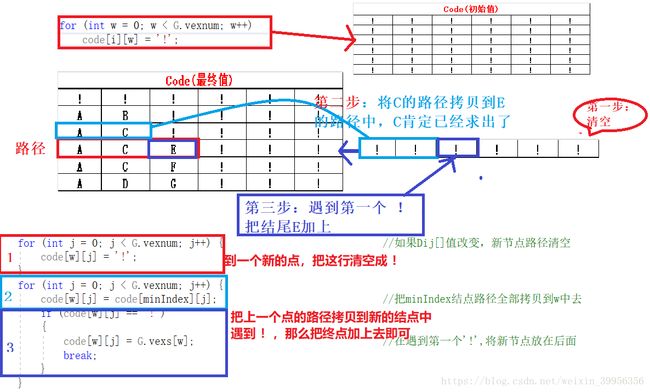
补充:这里再多说一句,动态二维数组分配
######先分配行,后分配列
typedef char **shortestCode; //最短路径编码
/******************************************************************
** 动态分配二维数组
*******************************************************************/
code = (shortestCode)malloc(G.vexnum * sizeof(char *)); //分配G.vexnum行
for (int i = 0; i < G.vexnum; ++i) { //为每行分配G.vexnum列
code[i] = (char *)malloc(G.vexnum * sizeof(char));
}
相关代码
/***********************************************************************************************
** 迪杰斯特拉(Dijkstra)算法
** v0 :任给一个起始点
** &code:最短路径线路(这里的&是必须的,如果没有,相当于传进来没有初始化的实体,编译器报错)
************************************************************************************************/
void ShortestPath_DIJ(MGraph &G, char v0, shortestCode &code)
{
int v0Index = LocateVex(G, v0);
bool *isGetShortestPath = (bool *)malloc(G.vexnum * sizeof(bool)); //是否并入S集
int *Dij = (int *)malloc(G.vexnum * sizeof(int)); //最短路径和
/******************************************************************
** 动态分配二维数组
*******************************************************************/
code = (shortestCode)malloc(G.vexnum * sizeof(char *)); //分配G.vexnum行
for (int i = 0; i < G.vexnum; ++i) { //为每行分配G.vexnum列
code[i] = (char *)malloc(G.vexnum * sizeof(char));
}
for (int i = 0; i < G.vexnum; i++) { //初始所有点都不并入S集,把顶点的权值赋给Dij[]
isGetShortestPath[i] = false;
Dij[i] = G.arcs[v0Index][i].wight;
for (int w = 0; w < G.vexnum; w++)
code[i][w] = '!'; //设code[][]初值为!,即没有路径
if (Dij[i] < INT__MAX)
{
code[i][0] = v0; //到i最短路径经过的第一个顶点是v0
code[i][1] = G.vexs[i]; //到i最短路径经过的第二个顶点是i
}
}
isGetShortestPath[v0Index] = true; //把顶点并入S集
int min, minIndex;
for (int i = 1; i < G.vexnum; i++) {
min = INT__MAX; //不妨把min放置为最大值
/******************************************************************
** 获取Dij数组中最小值-----这是其他还没有并入S集 路径上的一个子集
** 对应的数组位置----------为方便下面从这结点出发的弧遍历找最小值
*******************************************************************/
for (int w = 0; w < G.vexnum; w++) {
if (!isGetShortestPath[w])
if (Dij[w] < min)
{
minIndex = w;
min = Dij[w];
}
}
isGetShortestPath[minIndex] = true; //把位置为minIndex的结点并入S集
for (int w = 0; w < G.vexnum; w++) { //如果有更小的路径,替换原来的路径和最小值
if (!isGetShortestPath[w] && (min + G.arcs[minIndex][w].wight < Dij[w]))
{
Dij[w] = min + G.arcs[minIndex][w].wight; //更新Dij[]值
for (int j = 0; j < G.vexnum; j++) { //如果Dij[]值改变,新节点路径清空
code[w][j] = '!';
}
for (int j = 0; j < G.vexnum; j++) {
code[w][j] = code[minIndex][j]; //把minIndex结点路径全部拷贝到w中去
if (code[w][j] == '!')
{
code[w][j] = G.vexs[w]; //在遇到第一个'!',将新节点放在后面
break;
}
}
}
}
}
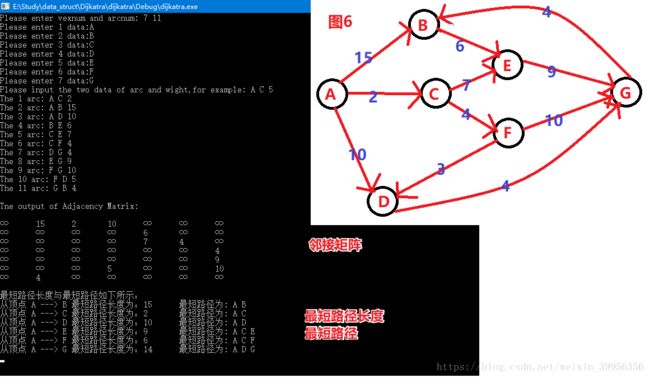
printf("\n迪杰斯特拉(Dijkstra)最短路径长度与最短路径如下所示:\n");
for (int i = 1; i < G.vexnum; i++) {
if (Dij[i] != INT__MAX)
{
printf("从顶点 %c ---> %c 最短路径长度为:%d\t最短路径为:", v0, G.vexs[i], Dij[i]);
for(int j = 0; j < G.vexnum; j++)
{
if(code[i][j] != '!')
printf(" %c",code[i][j]); //输出最短路径
}
printf("\n");
}
else if (Dij[i] == INT__MAX)
{
printf("从顶点 %c ---> %c 不可到达!!!\n", v0, G.vexs[i]); //不存在最短路径
}
}
free(Dij); //释放Dij[][]空间
free(isGetShortestPath); //释放isGetShortestPath[]空间
}
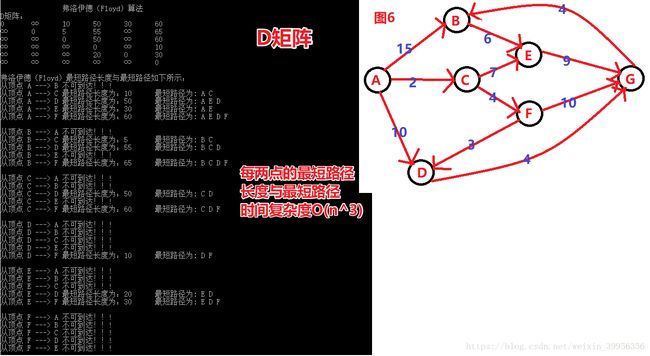
####三:弗洛伊德(Floyd)算法,带输出路径
和dijkstra算法一样,自己将这个算法分成两部分:
一:最短路径长度
二:最短路径
####首先,我们先看最短路径长度问题
这个算法的最短路径长度核心代码只有5行
1:就是看走哪边短!!!如果短就替换。

####其次,最短路径(弗洛伊德输出路径要麻烦些)
####一:路径的创建
####1:Path[ ][ ]初始化
矩阵Path的初值则为各个边的终点顶点-----相当于直接从v到w(上面两种方案的第一种)
![]()
####2:Path[ ][ ]逐渐储存路径
当且仅当通过“另外一个点”的时候,有更短路径,即更新路径Path[v][w],把“另外一个点”放进Path[v][w]里

这里举个例子:比如A->D,路径是A->E->D
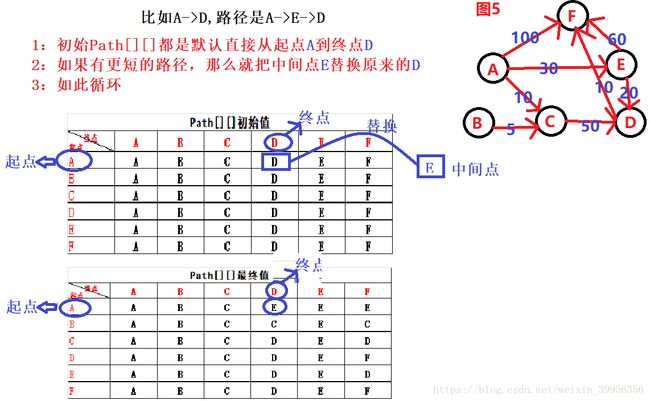
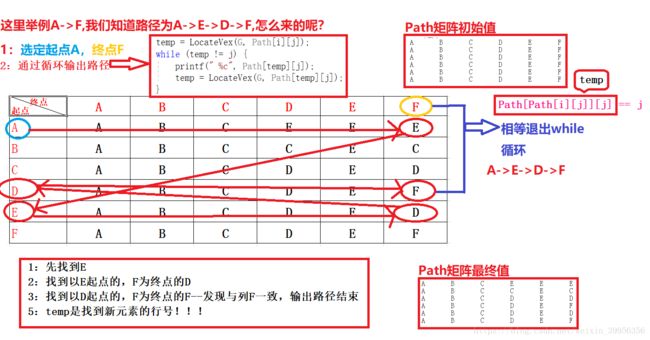
####二:路径的输出
这里主要是是一个循环,只到输出字母是终点为止。
![]()
不防先人为的输出起点,和第一个点,剩下的交给while循环

最后举个例子:比如A->F,路径是A->E->D->F
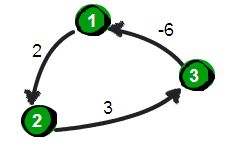
需要注意的是:Floyd-Warshall算法不能解决带有“负权回路”(或者叫“负权环”)的图
问题。因为带有“负权回路”的图没有最短路。比如:
相关代码
/*************************************************************************************************************
** 弗洛伊德(Floyd)算法
** 核心:是一种尝试的想法,从v到w只有两种方案:
1:直接从v到w,即DFloyd[v][w]
2:经过“另外的一个点”u,从v到w,即DFloyd[v][u] + DFloyd[u][w]
比较两种方案,取更小的
1:比较 :DFloyd[v][u] + DFloyd[u][w] < DFloyd[v][w]
2:取更小的:DFloyd[v][w] = DFloyd[v][u] + DFloyd[u][w]
** 这里的Path矩阵的构造很巧,关于Path矩阵代码仅仅只有几行而已!!!下面分析Path矩阵
1:矩阵Path的初值则为各个边的终点顶点-----相当于直接从v到w(上面两种方案的第一种)
2:当且仅当通过“另外一个点”的时候,有更短路径,即更新路径Path[v][w],把“另外一个点”放进Path[v][w]里
** 路径输出
1:不防把起点(G.vexs[i]),和Path[i][j]先输出(Path[i][j]是路径的第一个点)
2:循环输出直到(Path[temp][j] == j)为止!!!
** 自己可能还没有讲清楚,不用担心我在画个图解释下
请参考:https://mp.csdn.net/mdeditor/80579845
****************************************************************************************************************/
void ShortestPath_FLOYD(MGraph &G, shortestCode &Path)
{
//最短路径长度DFloyd[][]
int **DFloyd = (int **)malloc(G.vexnum * sizeof(int *)); //动态二维数组DFloyd[][],分配G.vexnum行
for (int i = 0; i < G.vexnum; ++i) { //为每行分配G.vexnum列
DFloyd[i] = (int *)malloc(G.vexnum * sizeof(int));
}
//最短路径Path[][]
Path = (shortestCode)malloc(G.vexnum * sizeof(char *)); //动态二维数组Path[][],分配G.vexnum行
for (int i = 0; i < G.vexnum; ++i) { //为每行分配G.vexnum列
Path[i] = (char *)malloc(G.vexnum * sizeof(char));
}
for (int v = 0; v < G.vexnum; v++)
for (int w = 0; w < G.vexnum; w++) {
if (v == w) //这里把主对角线权值变为0,不然主对角线会错,因为之前赋值的∞,举个例子B->B,现有B->C + C->B之和肯定小于∞,所以主对角线发生错误
G.arcs[v][w].wight = 0;
DFloyd[v][w] = G.arcs[v][w].wight; //把初始值存入DFloyd[][]
Path[v][w] = G.vexs[w]; //矩阵Path的初值则为各个边的终点顶点
}
printf("Path矩阵:\n");
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++)
printf("%c\t", Path[i][j]);
printf("\n");
}
/******************************************************************
** u:经过另外一个点
** v:起点
** w:终点
*******************************************************************/
for (int u = 0; u < G.vexnum; u++)
for (int v = 0; v < G.vexnum; v++)
for (int w = 0; w < G.vexnum; w++)
if (DFloyd[v][u] + DFloyd[u][w] < DFloyd[v][w]) { //比较两种方案,取更小的
DFloyd[v][w] = DFloyd[v][u] + DFloyd[u][w];
Path[v][w] = Path[v][u]; //更新Path矩阵
}
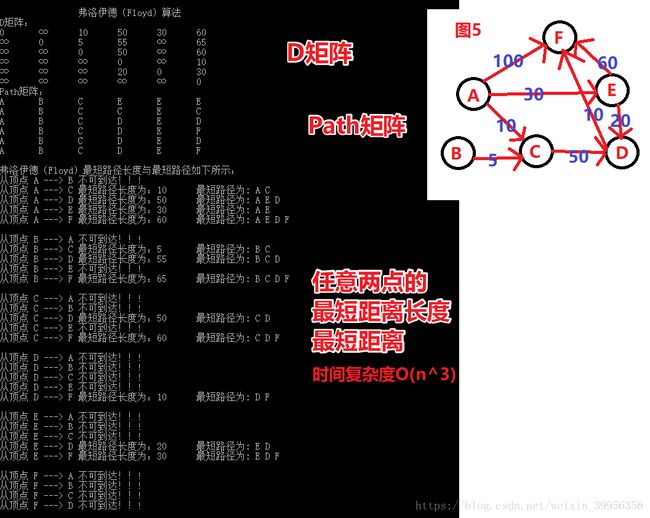
printf("\n\t\t弗洛伊德(Floyd)算法\nD矩阵:\n");
for (int i = 0; i < G.vexnum; i++){
for (int j = 0; j < G.vexnum; j++)
if (DFloyd[i][j] < INT__MAX)
printf("%d\t", DFloyd[i][j]);
else
printf("∞\t");
printf("\n");
}
printf("Path矩阵:\n");
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++)
printf("%c\t", Path[i][j]);
printf("\n");
}
printf("\n弗洛伊德(Floyd)最短路径长度与最短路径如下所示:\n");
/***************************************************************************************
** 这里输出除自己到自己的所有路径
** temp:通过Path[i][j] ---找到--> Path[Path[i][j]][j]<---判断是否相等-->j
****************************************************************************************/
for (int i = 0; i < G.vexnum; i++)
{
int temp = 0;
for (int j = 0; j < G.vexnum; j++) {
if(DFloyd[i][j] != INT__MAX)
{
if (j != i) //这里不需要输出自己到自己的路径
printf("从顶点 %c ---> %c 最短路径长度为:%d\t最短路径为: %c %c", G.vexs[i], G.vexs[j], DFloyd[i][j], G.vexs[i], Path[i][j]); //不防把起点(G.vexs[i]),和Path[i][j]先输出(Path[i][j]是路径的第一个点)
}else if (DFloyd[i][j] == INT__MAX)
{
printf("从顶点 %c ---> %c 不可到达!!!", G.vexs[i], G.vexs[j]); //不存在最短路径
}
temp = LocateVex(G, Path[i][j]);
while (temp != j) { //循环输出直到(Path[temp][j] == j)为止!!!
printf(" %c", Path[temp][j]); //输出最短路径
temp = LocateVex(G, Path[temp][j]);
}
if (j != i) //自己到自己不需要换行
printf("\n");
}
printf("\n"); //到某个点路径都显示了,换行
}
free(DFloyd); //释放DFloyd[][]空间
free(Path); //释放Path[][]空间
}
####主函数
#include "stdafx.h"
#include "dijkatra.h"
int main()
{
MGraph G; //有向图的邻接矩阵
shortestCode code; //编码--输出路径
printf("Please enter vexnum and arcnum: ");
scanf("%d %d", &G.vexnum, &G.arcnum); //输入结点数,弧数
CreatMGraph(G); //建立无向图的邻接矩阵
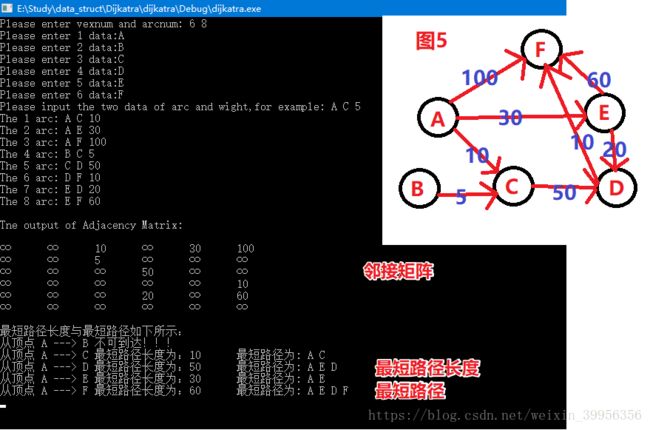
printf("\nTne output of Adjacency Matrix:\n\n");
printMatrixGraph(G); //输出邻接矩阵
ShortestPath_DIJ(G, G.vexs[0], code); //迪杰斯特拉(Dijkstra)算法--求得最短路径长度与最短路径
ShortestPath_FLOYD(G, code); //弗洛伊德(Floyd)算法--求得最短路径长度与最短路径
return 0;
}
####四:感谢与源代码(VS2017)
1:感谢一下波主文章对我的帮助,我相信他们的文章对你也会有帮助!!!
https://blog.csdn.net/qq_34374664/article/details/52261672
https://blog.csdn.net/txl199106/article/details/44980923
2:源代码(VS2017)
链接: https://pan.baidu.com/s/15kSoQhm2CTFHPN32OMez6g 提取码: w8va
3:如果你觉得本文还不错,请务必说明出处。