Coursera北大《数据结构基础》之栈与队列
本文基于Coursera北大课程《数据结构基础》,所有文中非标注图片均来自课件,侵删
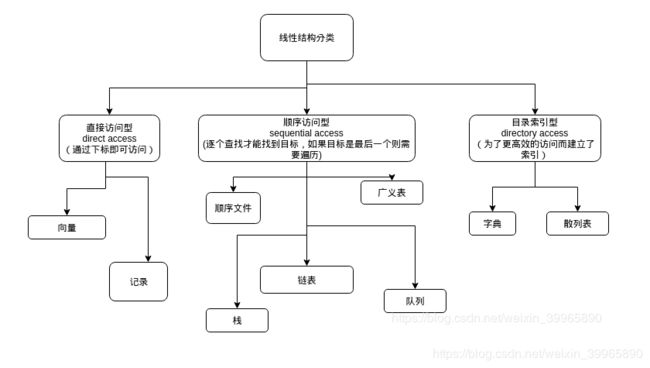
根据下图,通过访问形式划分的线性结构中,栈和队列属于顺序访问;按操作方式分,线性结构又可以划分为线性表、栈(LIFO)和队列(FIFO)三种形式,线性表在Coursera北大《数据结构基础》之线性表中已经学习过,这里进行栈和队列的学习。
目录
1. 栈(stack)
1.1 栈的实现方式
1.1.1 顺序栈(Array-based stack)
1.1.2 链式栈(linked stack)
1.1.3 顺序栈和链式栈的效率比较
2. 栈的应用
2.1 表达式求值
2.1.1 表达式的递归定义
2.1.2 中缀表达式求值
2.2 递归调用原理与递归转非递归
2.3. 函数调用
3. 队列(Queue)
3.1 队列的实现方式
3.1.1 顺序队列
3.1.2 链式队列
4. 队列的应用
参考文献
1. 栈(stack)
栈是一种后进先出(LIFO)限制访问端口的线性结构。栈的运算只在表的一端进行,主要操作包括进栈(push)和出栈(pop)。
P.S. 堆(heap)用于不符合LIFO的动态存储分配,如指针所指向空间的分配。
1.1 栈的实现方式
1.1.1 顺序栈(Array-based stack)
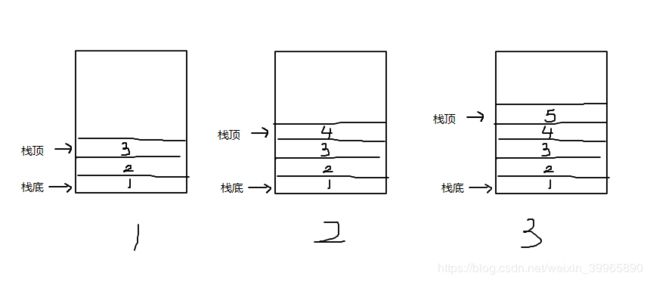
顺序栈使用向量表现,实质是简化的顺序表。使用顺序栈的关键是确定哪一端作为栈顶。如下图所示,顺序栈的栈顶是随着数据的进栈(也叫做压入栈顶)而改变的。
使用顺序栈时,要特别注意上溢和下溢问题:
- 上溢即overflow,是当栈中已经有maxsize个元素时,如果再做进栈运算,就会溢出;
- 下溢是underflow,即对空栈做出栈运算时会产生的现象。
1.1.2 链式栈(linked stack)
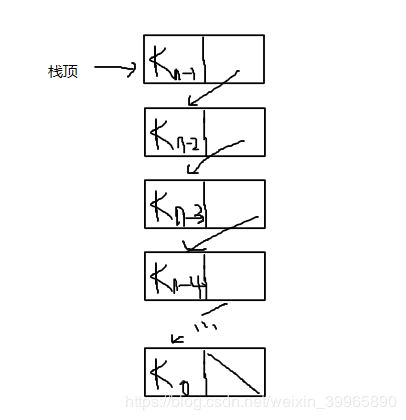
链式栈往往采用单链形式存储,指针从栈顶向下链接,如下图所示。
1.1.3 顺序栈和链式栈的效率比较
在时间效率上,顺序栈和链式栈的所有操作都只需要常数时间完成,没有明显差异;
在空间效率上,顺序栈必须声明一个固定长度,链式栈长度可变,但是增加了结构性开销。这一情况本质原因是线性表和链表的差异。
在实际应用中,顺序栈比链式栈应用更为广泛。这是因为一般来说栈不允许“读取内部元素”,只能在栈顶读,顺序栈更容易根据栈顶位置进行相对位移(读取内部元素的时间为O(1)),而链式栈需要根据指针在内部游走读取(读取内部元素时间为O(k),k为第k个要被读取的元素)。
2. 栈的应用
栈的后进先出体现了元素之间的透明性,所以常用来处理具有递归结构的数据。具体应用有:
- 表达式求值
- 消除递归
- 深度优先搜索
- 子程序/函数调用的管理
2.1 表达式求值
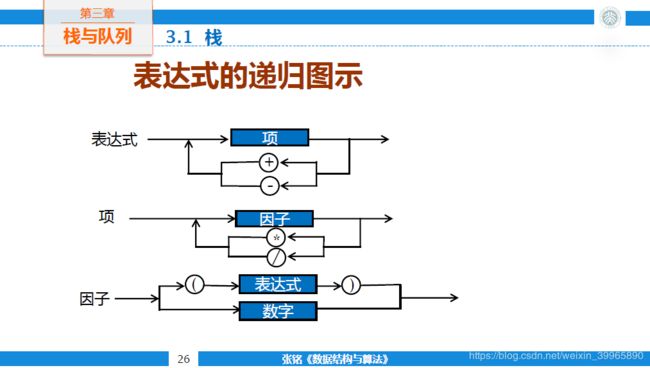
2.1.1 表达式的递归定义
(1)基本符号集
{0, 1, ..., 9, +, -, *, /, (, )}
(2)语法成分集
{<表达式>,<项>,<因子>,<常数>,<数字>}
(3)中缀表达式
中缀表达式其实就是四则运算。
前缀、中缀、后缀表达式都是对表达式的记法,因此也被称为前缀记法、中缀记法和后缀记法。
它们之间的区别在于运算符相对与操作数的位置不同:前缀表达式的运算符位于与其相关的操作数之前;中缀和后缀同理。
举例:
(3 + 4) × 5 - 6 就是中缀表达式
- × + 3 4 5 6 前缀表达式
3 4 + 5 × 6 - 后缀表达式
---------------------
作者:antineutrino
来源:CSDN
原文:https://blog.csdn.net/Antineutrino/article/details/6763722
版权声明:本文为博主原创文章,转载请附上博文链接!
与前缀表达式(例:+ 3 4)或后缀表达式(例:3 4 +)相比,中缀表达式不容易被电脑解析,但仍被许多程序语言使用,因为它符合人们的普遍用法。 与前缀或后缀记法不同的是,中缀记法中括号是必需的。 计算过程中必须用括号将操作符和对应的操作数括起来,用于指示运算的次序。
——摘自维基百科《中缀表达式》【1】
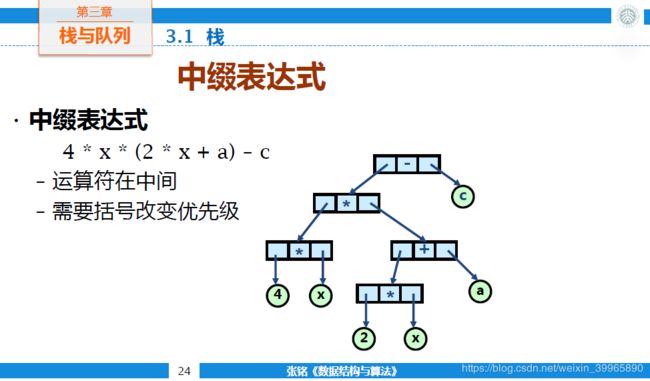
2.1.2 中缀表达式求值
其实就是二叉树的一个遍历,在后面学了二叉树之后再回来看这个例子会更清晰。
2.2 递归调用原理与递归转非递归
对于阶乘问题,使用非递归方法的代码编写是很容易的;但是对于河内塔这一类复杂问题,就比较麻烦了,需要用到深度搜索算法的思想,不断缩小问题的规模。
汉诺塔(港台:河内塔)是根据一个传说形成的数学问题:
有三根杆子A,B,C。A杆上有 N 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
提示:可将圆盘临时置于 B 杆,也可将从 A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则。
问:如何移?最少要移动多少次?
——摘自维基百科《汉诺塔》【2】
深度搜索可以概括为“退一步海阔天空”,即从第一层开始,在允许条件下进行下一层的搜索,当下一层的搜索不满足条件时,就返回上一层查看是否可以改变该层的情况让下一层符合条件,如此遍历直至所有层满足条件。
在使用递归时要注意保存上一层的内容。
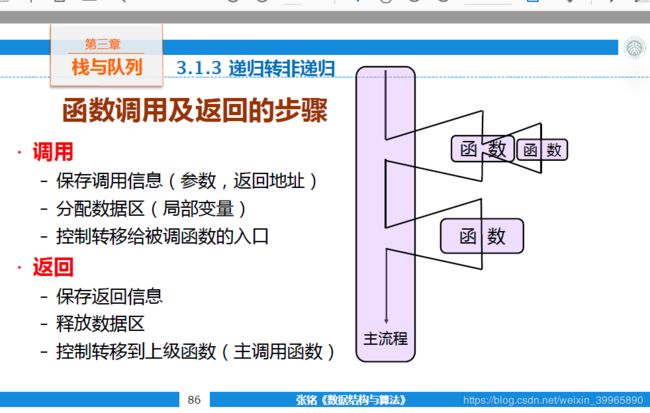
2.3. 函数调用
3. 队列(Queue)
队列是先进先出(FIFO)限制访问点的线性表。队列的运算只在表的两端进行(所有插入在表的一端进行,所有删除在另一端进行),因此其主要元素是队头和队尾(front and rear)。队列的主要操作是入队和出队(enQueue, deQueue)。
3.1 队列的实现方式
顺序队列和链式队列都不允许访问内部元素。
3.1.1 顺序队列
顺序队列可以是环形的,如下图所示。空队列对应下图左边的环,此时rear是在front前的;非空队列对应下图右边的环,元素从front开始逆时针插入,在插入到k5时该队列已满(虽然还有一格为空,但是为了区分空队列和非空队列,该格不插入元素)。
顺序队列关键是防止假溢出。
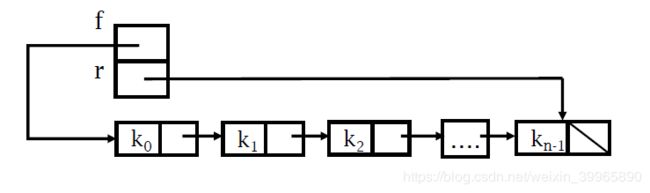
3.1.2 链式队列
链式队列也是用单链来实现,链接指针的方向是从队列的前端向尾端链接。
——摘自课程
4. 队列的应用
只要满足FIFO性质的应用都可以用队列作为其数据组织方式或中间数据结构。很多硬件通信设备都是使用队列来管理。
参考文献
【1】https://zh.wikipedia.org/wiki/%E4%B8%AD%E7%BC%80%E8%A1%A8%E7%A4%BA%E6%B3%95
【2】https://zh.wikipedia.org/wiki/%E6%B1%89%E8%AF%BA%E5%A1%94