矩阵乘法的分块优化
普通矩阵乘法一般采用3重循环完成。
void dgemm (int n, double* A, double* B, double* C)
{
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
{
double cij = C[i+j*n]; /* cij = C[i][j] */
for(int k = 0; k < n; k++ )
cij += A[i+k*n] * B[k+j*n]; /* cij += A[i][k]*B[k][j] */
C[i+j*n] = cij; /* C[i][j] = cij */
}
}
下面在以上基础探究:
1、矩阵乘法与cache容量的关系
2、分块优化
3、优化前后对比
4、分块大小与性能的关系
1、普通矩阵乘法访存时高速缓存缺失与矩阵大小n和cache容量的关系
cache不变,矩阵越大,越难装进cache中,高速缓存缺失将缺失更多
矩阵大小不变,cache越大,越容易装更多的数据,高速缓存缺失将缺失更少
2、充分利用高速缓存的局部性将矩阵乘法分块实现,优化性能
完成do_block子程序的设计和相关性能测试程序的代码
| inline void do_block (int n, double *A, double *B, double *C) { for(int i = 0; i < BLOCKSIZE; i++) { for(int j = 0; j < BLOCKSIZE; j++) { double cij = C[i*n+j]; for(int k = 0; k < BLOCKSIZE; k++ ) cij +=A[i*n+k] * B[k*n + j]; C[i*n+j] = cij; } } }
inline void dgemm_block (int n, double* A, double* B, double* C) { for ( int sj = 0; sj < n; sj += BLOCKSIZE ) for ( int si = 0; si < n; si += BLOCKSIZE ) for ( int sk = 0; sk < n; sk += BLOCKSIZE ) do_block(n, A+si*n+sk, B+sk*n+sj, C+si*n+sj); } |
分块矩阵乘法的子块计算和正常的矩阵乘法是一样的,只不过在分块的时候传给函数的矩阵起始地址会有变化,需要变化为对应块的起始地址
3、测试分块版本矩阵计算在矩阵不同大小时与未分块版本的性能对比。
L1缓存所能容纳的矩阵数组长度为 256*1024÷8÷3 = 10816
L2缓存所能容纳的矩阵数组长度为 1*1024*1024÷8÷3 = 43690
L3缓存所能容纳的矩阵数组长度为 6*1024*1024÷8÷3 = 262144
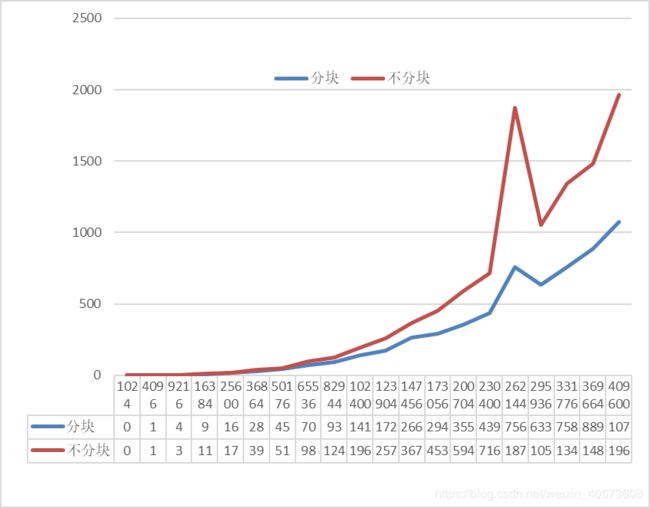
如上图,横坐标代表数组长度(即矩阵里元素的个数,从1024到409600,囊括了L1、L2、L3三个缓存的大小),纵坐标代表矩阵乘法的时间
现象:
在矩阵 小于 L1缓存的时候的时候,分块比不分块 慢
在矩阵 大于 L1缓存的时候的时候,分块比不分块 快
分析:
在矩阵大小小于L1缓存的时候的时候,矩阵可以完全装到cache中,所以2种方法速度差不多,但是由于分块有多余的函数调用开销,所以分块会比不分块慢些
在矩阵大小大于L1缓存的时候的时候,不分块矩阵没法完全装进L1缓存中,,而分块矩阵可以装进L1缓存中,所以不分块矩阵乘法会比分块矩阵乘法慢
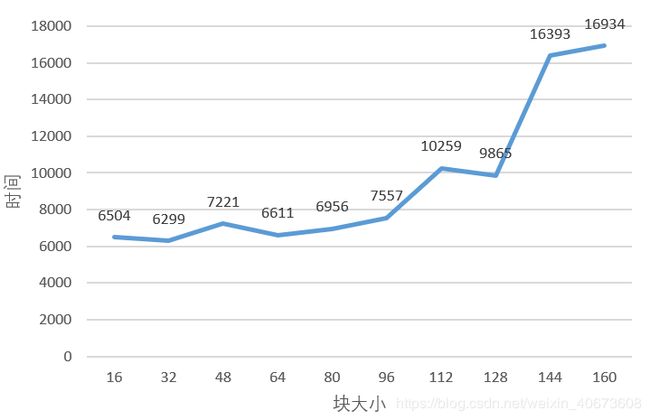
4、固定矩阵大小为足够大,调整BLOCKSIZE大小,分析BLOCKSIZE大小对性能的影响
如上图,矩阵大小固定为1024*1024(足够大),横坐标代表分块的大小,纵坐标代表矩阵乘法的时间
现象:
分块大小在100以内,矩阵乘法的时间差不多,分块大小超过100以后,矩阵乘法的时间明显变长
分析:
图中的分块大小都是可以装进L1缓存的,但不同的分块大小仍然会有差异,原因是即便数据可以装进L1缓存中,但因块的大小不同,cache命中的效率也会有所不同
当分块大小在比较小的时候,cache命中的时间基本差不多,所以矩阵乘法的时间差不多
当分块大小越来越大的时候,cache命中的时间变长,所以矩阵乘法时间会变逐渐变慢