机器学习-逻辑回归(python3代码实现)

逻辑回归（Logistic regression）

哈尔滨工程大学—537

算法原理

一、sigmoid函数

线性回归是将一组输入映射为一个输出值：
hθ(x)=θ0+θ1x1+θ1x2 h θ ( x ) = θ 0 + θ 1 x 1 + θ 1 x 2 ，其中 θ0 θ 0 是偏置项。
我们的目的是要找到最合适的 θ0，θ1，θ2， θ 0 ， θ 1 ， θ 2 ， 使对于每一组输入的特征向量 x1，x2 x 1 ， x 2 ，都能使上述函数的函数值尽可能的接近真实值。

那么逻辑回归就是在此基础上再把线性回归得到的函数值映射为一个0到1之间的概率值，如果这个概率值特别大，就说明该样本属于该类别。

那么如何能将一个 (−∞,+∞) ( − ∞ , + ∞ ) 之间的任意数值映射为一个 (0,1) ( 0 , 1 ) 之间的函数值，这里就引入了sigmoid函数：

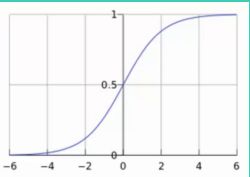
g(z)=11+e−z g ( z ) = 1 1 + e − z ， 函数图像如下。

于是每一组的 θ0,θ1,θ2 θ 0 , θ 1 , θ 2 和 1,x1,x2 1 , x 1 , x 2 结合之后的值都可以作为sigmoid函数的自变量，最后经sigmoid函数映射出一个 (0,1) ( 0 , 1 ) 区间的概率值。

于是我们可以将其整合为一个函数：
hθ(x)=g(θTx)=11+e−θTx h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x ，这个函数所表达的含义就是找到合适的 θ θ ，使其与 x x 结合再经sigmoid函数映射后得到一个 (0,1) ( 0 , 1 ) 区间的概率值。这里 θ θ 和 x x 分别是 n n 维列向量。

二、概率分类

于是我们要做的0,1分类任务可以用如下概率来表示：
P(y=1|x;θ)=hθ(x) P ( y = 1 | x ; θ ) = h θ ( x ) ①
P(y=0|x;θ)=1−hθ(x) P ( y = 0 | x ; θ ) = 1 − h θ ( x ) ②

将其整合为一个函数即：
P(y|x;θ)=(hθ(x))y(1−hθ(x))1−y P ( y | x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y
当y=0时，则为①式；y=1时，则为②式。

三、最大似然和梯度下降

于是我们通过该算法要达到的目的就是找到最合适的 θ θ ，使其与 x x 结合之后 P(y|x;θ) P ( y | x ; θ ) 这个概率值尽可能的大。

如果一共有m个样本，那么若每个样本的 P(y|x;θ) P ( y | x ; θ ) 最大，则 ∏mi=1P(y|x;θ) ∏ i = 1 m P ( y | x ; θ ) 最大，
也就是求：
L(θ)=∏mi=1(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i) L ( θ ) = ∏ i = 1 m ( h θ ( x ( i ) ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) 的最大值。

将其进行一次log函数映射变换，转化为求：
l(θ)=logL(θ)=∑mi=1(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))) l ( θ ) = log ⁡ L ( θ ) = ∑ i = 1 m ( y ( i ) log ⁡ h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ⁡ ( 1 − h θ ( x ( i ) ) ) )

这里再引入一个 J(θ) J ( θ ) 函数，叫做代价函数，将所求最大值转化为求最小值：
J(θ)=−1ml(θ) J ( θ ) = − 1 m l ( θ ) ，于是我们所要做的就是求 J(θ) J ( θ ) 的最小值。

接下来对 θ θ 求导，得到：
dJ(θ)dθj=1m∑mi=1(hθ(x(i))−y(i))x(i)j d J ( θ ) d θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

最后通过不断更新参数 θ θ 找到最小值：
θj=θj−αdJ(θ)dθj=θj−α1m∑mi=1(hθ(x(i))−y(i))x(i)j θ j = θ j − α d J ( θ ) d θ j = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )

为什么通过 θj=θj−αdJ(θ)dθj θ j = θ j − α d J ( θ ) d θ j 的方式能够找到函数的最小值呢？
如图：

当 J(θ) J ( θ ) 的导数大于0时，将 θ θ 减小一点点， J(θ) J ( θ ) 就减小一点点，同理，当 J(θ) J ( θ ) 的导数大于0时，将 θ θ 增大一点点， J(θ) J ( θ ) 就减小一点点。而这里所说的一点点就是步长 α α 。

python3代码实现

一、定义主要功能函数

1)根据上述算法，首先要将sigmoid函数定义出来：

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

2)在sigmoid函数基础上定义出 hθ(x) h θ ( x ) 函数，其中X为特征矩阵：

def model(X, theta):
    return sigmoid(np.dot(X, theta.T))

3)定义出代价函数 J(θ) J ( θ ) ，其中X为特征矩阵，y为类标签向量：

def cost(X, y, theta):
    left = np.multiply(-y,np.log(model(X, theta)))
    right = np.multiply(1 - y, np.log(1 - model(X, theta)))
    return np.sum(left - right) / X.shape[0]

4)再定义出对 θ θ 的导数，即 dJ(θ)dθj d J ( θ ) d θ j 的函数。

def gradient(X, y, theta):
    grad = np.zeros((theta.shape))
    error = (model(X, theta) - y).ravel()
    for j in range(theta.shape[1]):
        term = np.multiply(error, X[:,j])
        grad[0,j] = np.sum(term) / len(X)
    return grad

5)在寻找 J(θ) J ( θ ) 最小值的过程中，不会无限次的迭代下去，所以我们需要定义在什么时候停止迭代，这里定义了三种停止策略：

STOP_ITER = 0
STOP_COST = 1
STOP_GRAD = 2
#三种停止策略
def stopCriterion(stopType, value, threshold):
    if stopType == STOP_ITER:   return value > threshold
    elif stopType == STOP_COST:  return abs(value[-1]-value[-2]) < threshold
    elif stopType == STOP_GRAD:   return np.linalg.norm(value) < threshold

6)在实际应用中，我们的数据经常是有规律采集的，比如样本1~100是采集的女生的身高、体重、体脂比等特征，而101~200是采集的男生的相应的特征，所以我们需要将样本的顺序打乱，以保证学习效果。这里我们定义了一个样本顺序洗牌函数：

import numpy.random
#洗牌
def shuffleData(data):
    np.random.shuffle(data)
    cols = data.shape[1]
    X = data[:,0:cols-1]
    y = data[:,cols-1:cols]
    return X, y

这样我们就把几个主要的函数定义完了，接下来我们就可以根据算法的流程，依次调用各个函数，最终实现我们的目标。

7)接下来开始编写实现主体功能的函数：

import time
def descent(data, theta, batchSize, stopType, threshold, alpha):
    #梯度下降求解

    init_time = time.time()
    i = 0  #迭代次数
    k = 0  #batch，一次进行求导的样本个数
    X, y = shuffleData(data)
    grad = np.zeros((theta.shape))  #计算的梯度，初始值为0向量
    costs = [cost(X, y, theta)]   #损失函数值

    while True:
        grad = gradient(X[k:k+batchSize], y[k:k+batchSize], theta)
        k += batchSize   #取batch数量个数据
        if k >= X.shape[0]:
            k = 0
            X, y = shuffleData(data)     #重新洗牌
        theta = theta - alpha*grad       #参数更新
        costs.append(cost(X, y, theta))  #计算新的损失值
        i += 1

        if stopType == STOP_ITER:   value = i
        elif stopType == STOP_COST:  value = costs
        elif stopType == STOP_GRAD:  value = grad
        if stopCriterion(stopType, value, threshold): break

    return theta, i, costs, grad, time.time() - init_time    

8)最后分别用 theta,i,costs,grad,time t h e t a , i , c o s t s , g r a d , t i m e 变量来接收 descent d e s c e n t 函数的返回值。（这里 descent d e s c e n t 函数的实参分别为：原始数据， θ θ 初始值，每次选50个样本进行求导，停止策略为STOP_INTER，迭代一万次，学习步长 α α 为0.00001）：

theta, i, costs, grad, time = descent(orig_data, theta, 50, STOP_ITER, 10000, 0.00001)
print(theta, time)

9)最后利用 matplotlib m a t p l o t l i b 库下的 pyplot p y p l o t 绘制一下 cost c o s t 函数值的下降曲线，即 J(θ) J ( θ ) 的下降曲线：

fig, ax = plt.subplots(figsize=(12,4))
ax.plot(np.arange(len(costs)), costs, "r")

于是得到如下图像：

这里的横坐标为迭代次数，纵坐标为损失函数值。可以看到，损失函数值随着迭代次数的增加不断减小。当迭代次数达到10000次时，损失函数值接近最小值0.60。

以上就是逻辑回归算法的基本原理，此致敬礼。