机器学习面试点杂记
本文用于自己整理机器学习相关概念与原理,如有错误欢迎在评论里指正!~
文章目录
- 熵
- 参数模型与非参数模型
- SVM
- 1. 原始问题
- 2. 拉格朗日函数
- 3. 对偶问题
- 4. 转化为对偶问题的好处
- 5. 合页损失函数
- 6. 多分类SVM
- 7. 高斯核函数
- LR
- 1. 二项逻辑回归
- 2. 多项逻辑回归(K项)
- 3. 损失函数
- 4. LR与SVM区别
- 树模型
- 1. 损失函数、树的剪枝
- 2. ID3、C4.5、CART
- 3. 剪枝
- 4. 连续值与缺失值处理
- 降维
- 1. PCA
- 2. LDA
- 集成学习
- 1. Boosting和Bagging(Bootstrap Aggregating),偏差与方差
- 2. GBDT与XGBoost
- KNN
- 聚类算法
- 性能度量
- DBSCAN
- ROC与AUC
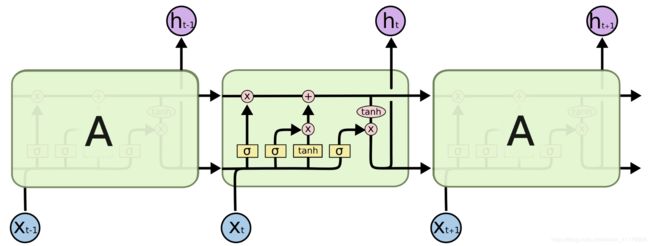
- LSTM
- 结构图
熵
- 信息量: I ( x i ) = − l o g ( p ( x i ) ) I(x_i)=-log(p(x_i)) I(xi)=−log(p(xi))
- 熵: H ( x ) = − ∑ i n p ( x i ) l o g ( p ( x i ) ) H(x)=-\sum_i^np(x_i)log(p(x_i)) H(x)=−∑inp(xi)log(p(xi))
- KL散度(相对熵): D K L ( p ∣ ∣ q ) = ∑ i n p ( x i ) ( I q ( x i ) − I p ( x i ) ) ) = ∑ i n p ( x i ) l o g p ( x i ) q ( x i ) = − H ( x ) + [ − ∑ i n p ( x i ) l o g ( q ( x i ) ) ] D_{KL}(p||q)=\sum_i^np(x_i)(I_q(x_i)-I_p(x_i)))=\sum_i^np(x_i)log\frac{p(x_i)}{q(x_i)}=-H(x)+[-\sum_i^np(x_i)log(q(x_i))] DKL(p∣∣q)=∑inp(xi)(Iq(xi)−Ip(xi)))=∑inp(xi)logq(xi)p(xi)=−H(x)+[−∑inp(xi)log(q(xi))]
- 交叉熵: H ( p , q ) = − ∑ i n p ( x i ) l o g ( q ( x i ) ) H(p,q)=-\sum_i^np(x_i)log(q(x_i)) H(p,q)=−∑inp(xi)log(q(xi))
- 互信息: g ( Y ∣ X ) = H ( Y ) − H ( Y ∣ X ) g(Y|X)=H(Y)-H(Y|X) g(Y∣X)=H(Y)−H(Y∣X)
- 信息增益: g ( D ∣ A ) = H ( D ) − H ( D ∣ A ) g(D|A)=H(D)-H(D|A) g(D∣A)=H(D)−H(D∣A)
- 信息增益比: g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A)=\frac{g(D,A)}{H_A(D)} gR(D,A)=HA(D)g(D,A),其中 H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ H_A(D)=-\sum_{i=1}^n\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|} HA(D)=−∑i=1n∣D∣∣Di∣log2∣D∣∣Di∣为数据集 D D D关于特征 A A A的熵
参数模型与非参数模型
参考博客
SVM
几何间隔: γ = 2 ∣ ∣ ω ∣ ∣ \gamma=\frac{2}{||\omega||} γ=∣∣ω∣∣2
约束条件: y i ( ω T x i + b ) ≥ 1 , ( i = 1 , 2 , . . . , m ) y_i(\omega^Tx_i+b)\geq1, ( i=1,2,...,m) yi(ωTxi+b)≥1,(i=1,2,...,m)
1. 原始问题
硬间隔(结构风险):
- min ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 \min_{\omega,b} \frac{1}{2}||\omega||^2 minω,b21∣∣ω∣∣2
- y i ( ω T x i + b ) ≥ 1 , ( i = 1 , 2 , . . . , m ) y_i(\omega^Tx_i+b)\geq1, ( i=1,2,...,m) yi(ωTxi+b)≥1,(i=1,2,...,m)
软间隔(结构风险+经验风险):
- min ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 m ξ i \min_{\omega,b} \frac{1}{2}||\omega||^2+C\sum_{i=1}^m\xi_i minω,b21∣∣ω∣∣2+C∑i=1mξi
- y i ( ω T x i + b ) ≥ 1 − ξ i , ( i = 1 , 2 , . . . , m ) y_i(\omega^Tx_i+b)\geq1-\xi_i, ( i=1,2,...,m) yi(ωTxi+b)≥1−ξi,(i=1,2,...,m)
2. 拉格朗日函数
拉格朗日函数: L ( ω , b , α ) = 1 2 ∣ ∣ ω ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( ω T x i + b ) ) L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^Tx_i+b)) L(ω,b,α)=21∣∣ω∣∣2+∑i=1mαi(1−yi(ωTxi+b))
拉格朗日原始问题: min ω , b max α L ( ω , b , α ) \min_{\omega,b}\max_\alpha L(\omega,b,\alpha) minω,bmaxαL(ω,b,α)
拉格朗日对偶问题: max α min ω , b L ( ω , b , α ) \max_\alpha\min_{\omega,b} L(\omega,b,\alpha) maxαminω,bL(ω,b,α)
3. 对偶问题
L ( ω , b , α ) L(\omega,b,\alpha) L(ω,b,α)分别对 ω \omega ω和 b b b求偏导:
ω = ∑ i = 1 m α i y i x i \omega=\sum_{i=1}^m\alpha_iy_ix_i ω=∑i=1mαiyixi
0 = ∑ i = 1 m α i y i 0=\sum_{i=1}^m\alpha_iy_i 0=∑i=1mαiyi
硬间隔对偶问题即为:
- max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m α i α j y i y j x i T x j \max_{\alpha} \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j maxα∑i=1mαi−21∑i=1mαiαjyiyjxiTxj
- 对于 i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m:
- ∑ i = 1 m α i y i = 0 \sum_{i=1}^m\alpha_iy_i=0 ∑i=1mαiyi=0
- α i ≥ 0 \alpha_i\geq 0 αi≥0
软间隔对偶问题即为:
- max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m α i α j y i y j x i T x j \max_{\alpha} \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j maxα∑i=1mαi−21∑i=1mαiαjyiyjxiTxj
- 对于 i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m:
- ∑ i = 1 m α i y i = 0 \sum_{i=1}^m\alpha_iy_i=0 ∑i=1mαiyi=0
- C ≥ α i ≥ 0 C\geq \alpha_i\geq 0 C≥αi≥0
4. 转化为对偶问题的好处
- 不等式约束转化为等式约束
- 方便引入核函数
- 降低问题复杂度:
a. 原始问题中,复杂度与样本的维度 ω \omega ω有关;对偶问题中,复杂度只与样本数量 m m m有关。
b. 系数 α \alpha α仅在支持向量中非0,其它全部为0。
5. 合页损失函数
软间隔最大化,则有合页损失函数: L ( y ( ω x + b ) ) = [ 1 − y ( ω x + b ) ] + L(y(\omega x+b))=[1-y(\omega x+b)]_+ L(y(ωx+b))=[1−y(ωx+b)]+
优化目标为: min ∑ i = i m [ 1 − y i ( ω x i + b ) ] + + λ ∣ ∣ ω ∣ ∣ 2 \min \sum_{i=i}^m[1-y_i(\omega x_i+b)]_++\lambda||\omega||^2 min∑i=im[1−yi(ωxi+b)]++λ∣∣ω∣∣2
6. 多分类SVM
- ovr:训练 k k k个分类器,总体速度较快
- 训练单个模型时,相对速度较慢
- 类别不对称,可采用较大的惩罚因子C
- 当有新的类别加进来时,需要对所有的模型进行重新训练
- ovo:训练 k ( k − 1 ) 2 \frac{k(k-1)}{2} 2k(k−1)个分类器,总体速度较慢
- 在训练单个模型时,相对速度较快
- 当有新的类别加进来时,不需要重新训练所有的模型
7. 高斯核函数
参考博客
LR
1. 二项逻辑回归
对数几率为输入 x x x的线性函数: l o g i t ( P ( Y = 1 ∣ x ) ) = P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = ω x logit(P(Y=1|x))=\frac{P(Y=1|x)}{1-P(Y=1|x)}=\omega x logit(P(Y=1∣x))=1−P(Y=1∣x)P(Y=1∣x)=ωx
条件概率分布为:
- l o g i t ( P ( Y = 1 ∣ x ) ) = e ω x 1 + e ω x logit(P(Y=1|x))=\frac{e^{\omega x}}{1+e^{\omega x}} logit(P(Y=1∣x))=1+eωxeωx
- l o g i t ( P ( Y = 0 ∣ x ) ) = 1 1 + e ω x logit(P(Y=0|x))=\frac{1}{1+e^{\omega x}} logit(P(Y=0∣x))=1+eωx1
2. 多项逻辑回归(K项)
第 i i i项与第 K K K项的对数概率比: P ( Y = i ∣ x ) P ( Y = K ∣ x ) = ω i x \frac{P(Y=i|x)}{P(Y=K|x)}=\omega_i x P(Y=K∣x)P(Y=i∣x)=ωix
再根据总概率和为1,多项逻辑回归的条件概率分布为:
- l o g i t ( P ( Y = i ∣ x ) ) = e ω i x 1 + ∑ i = 1 K − 1 e ω x logit(P(Y=i|x))=\frac{e^{\omega_i x}}{1+\sum_{i=1}^{K-1}e^{\omega x}} logit(P(Y=i∣x))=1+∑i=1K−1eωxeωix
- l o g i t ( P ( Y = K ∣ x ) ) = 1 1 + ∑ i = 1 K − 1 e ω x logit(P(Y=K|x))=\frac{1}{1+\sum_{i=1}^{K-1}e^{\omega x}} logit(P(Y=K∣x))=1+∑i=1K−1eωx1
3. 损失函数
似然函数: ∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} ∏i=1N[π(xi)]yi[1−π(xi)]1−yi
对数似然: L ( ω ) = ∑ i = 1 N [ y i l n π ( x i ) + ( 1 − y i ) l n ( 1 − π ( x i ) ) ] L(\omega)=\sum_{i=1}^N[y_iln\pi(x_i)+(1-y_i)ln(1-\pi(x_i))] L(ω)=∑i=1N[yilnπ(xi)+(1−yi)ln(1−π(xi))]
损失函数: J ( ω ) = − 1 N ∑ i = 1 N [ y i l n π ( x i ) + ( 1 − y i ) l n ( 1 − π ( x i ) ) ] J(\omega)=-\frac{1}{N}\sum_{i=1}^N[y_iln\pi(x_i)+(1-y_i)ln(1-\pi(x_i))] J(ω)=−N1∑i=1N[yilnπ(xi)+(1−yi)ln(1−π(xi))],本质上就是衡量真实分布和预测分布之间的交叉熵
4. LR与SVM区别
- LR是参数模型,SVM是非参数模型。
- 从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss.这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
- SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
- 逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
- logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
树模型
- 信息增益: g ( D ∣ A ) = H ( D ) − H ( D ∣ A ) g(D|A)=H(D)-H(D|A) g(D∣A)=H(D)−H(D∣A)
- 信息增益比: g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A)=\frac{g(D,A)}{H_A(D)} gR(D,A)=HA(D)g(D,A),其中 H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ H_A(D)=-\sum_{i=1}^n\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|} HA(D)=−∑i=1n∣D∣∣Di∣log2∣D∣∣Di∣为数据集 D D D关于特征 A A A的熵
- 基尼指数: G i n i ( D ) = 1 − ∑ k = 1 K ( ∣ C k ∣ D ) 2 Gini(D)=1-\sum_{k=1}^K(\frac{|C_k|}{D})^2 Gini(D)=1−∑k=1K(D∣Ck∣)2, G i n i ( D , A ) = ∣ D 1 ∣ D G i n i ( D 1 ) + ∣ D 2 ∣ D G i n i ( D 2 ) Gini(D,A)=\frac{|D_1|}{D}Gini(D_1)+\frac{|D_2|}{D}Gini(D_2) Gini(D,A)=D∣D1∣Gini(D1)+D∣D2∣Gini(D2),越小越纯分类能力越好
1. 损失函数、树的剪枝
无修建的决策树损失函数: C ( T ) = ∑ t − 1 ∣ T ∣ N t H t ( T ) C(T)=\sum_{t-1}^{|T|}N_tH_t(T) C(T)=∑t−1∣T∣NtHt(T),其中 N t N_t Nt表示叶节点 t t t包含的样本点数, H t ( T ) H_t(T) Ht(T)为该叶节点的经验熵
修剪后的决策树的损失函数: C α ( T ) = C ( T ) + α ∣ T ∣ C_{\alpha}(T)=C(T)+\alpha|T| Cα(T)=C(T)+α∣T∣,其中 ∣ T ∣ |T| ∣T∣为叶节点个数, α \alpha α相当于正则化系数
2. ID3、C4.5、CART
ID3:根据信息增益从根结点开始递归选取,直至信息增益很小或特征用完,相当于一个极大似然过程。
C4.5:使用信息增益比进行特征选择
CART:(分类)使用基尼指数进行特征筛选,采用剪枝策略减少过拟合风险;(回归)最小二乘法迭代寻找最优划分特征的最优划分点,回归树参考博客
| 树模型 | 启发式函数 | 特征类型 | 任务类型 | 节点分支 | 特征复用 |
|---|---|---|---|---|---|
| ID3 | 信息增益 | 离散 | 分类 | 多分叉 | 否 |
| C4.5 | 信息增益比 | 离散/连续 | 分类 | 多分叉 | 否 |
| CART | 基尼指数 | 离散/连续 | 分类/回归 | 二分叉 | 是 |
3. 剪枝
- 预剪枝:欠拟合风险,何时停止需要根据数据特征经验判断(层数过多;节点样本数量过小;对测试集准确率提升过小)
- 后剪枝:CART剪枝方法CCP(代价复杂度剪枝,Cost Complexity Pruning),详见《百面机器学习》P68
- 在节点 t t t处剪枝后的误差增加率 α = R ( t ) − R ( T t ) ∣ L ( T t ) − 1 ∣ \alpha=\frac{R(t)-R(T_t)}{|L(T_t)-1|} α=∣L(Tt)−1∣R(t)−R(Tt)
- 从完整决策树 T 0 T_0 T0开始,每一步剪去带来最小误差增加率的节点,依次生成一系列子树 { T 0 , T 1 , . . . , T n } \{T_0,T_1,...,T_n\} {T0,T1,...,Tn},其中 T n T_n Tn为根节点
- 在所有子树序列中,进行 k k k折交叉验证,重复 N N N次,选取最优子树
4. 连续值与缺失值处理
连续值:某一连续值特征在样本 D D D上有 n n n种取值,选取 n − 1 n-1 n−1个中位数作为划分 n n n个区间
缺失值:未缺失值数据直接分类,权重为1;缺失值数据根据未缺失值每类的数量比例按照权重进入下一级的所有类中
降维
1. PCA
-
主成分分析(Principle Components Analysis):最大化投影方差 = 最小化平方误差
- 中心化处理
- 求协方差矩阵
- 特征值分解,从大到小排序
- 特征值即为投影后的方差;对应的特征向量即为投影方向
-
最大化方差推导如下:
- 原始m个样本的坐标: X = [ x 1 . . . x i . . . x m ] X=[x_1...x_i...x_m] X=[x1...xi...xm], x i x_i xi为第 i i i个样本
- 投影矩阵: W = [ w 1 . . . w j . . . w d ] W=[w_1...w_j...w_d] W=[w1...wj...wd], w j T x i w_j^Tx_i wjTxi表示 x i x_i xi在新坐标下第 j j j维的值
- 则投影后方差为: ∑ i W T x i x i T W \sum_iW^Tx_ix_i^TW ∑iWTxixiTW
- 优化目标为: max W t r ( W T X i X i T W ) \max_W tr(W^TX_iX_i^TW) maxWtr(WTXiXiTW)
- 约束条件: W T W = 0 W^TW=0 WTW=0
- 根据拉格朗日乘子法: X X T W = λ W XX^TW=\lambda W XXTW=λW
- 而 X X T XX^T XXT又为
2. LDA
- 线性判别分析(Linear Discriminant Analysis):最大化类间间距 + 最小化类内间距
集成学习
1. Boosting和Bagging(Bootstrap Aggregating),偏差与方差
Boosting串行(基分类器间强相关,不能减小方差)逐步聚焦误分类的样本,减小偏差
Bagging并行训练不完全相同的模型并多数投票,减小方差(基分类器最好采用不稳定的敏感模型,而非KNN、线性分类器等)
2. GBDT与XGBoost
| 名称 | 性质 | 正则化 | 损失函数 | 基分类器 | 数据范围 |
|---|---|---|---|---|---|
| GBDT | 机器学习算法 | 构建完决策树后进行剪枝 | 一阶导 | CART | 每轮迭代使用完整数据集 |
| XGBoost | 工程实现 | 构建阶段显式加入正则项 | 二阶泰勒展开 | 多种类型基分类器 | 可对数据采样 |
KNN
kd树的最近邻搜索步骤:
- 构造平衡kd树
- 从根节点出发,根据
待划分点的坐标范围搜索到叶节点,记为当前最近点 - 递归:
- 若
当前节点比当前最近点距离待划分点距离更小,则将当前最近点更新为当前节点 - 检查
当前节点的父节点的另一侧是否存在更近的点(即当前节点的父节点对应的超矩形是否与当前最近点表示的超球体相交):
a. 若存在,则从另一侧递归
b. 若不存在,则向父节点回退
- 若
- 直至根节点,搜索结束;此时
当前最近点即为待划分点的最近邻
聚类算法
性能度量
外部指标:与实际或者经验进行对比
内部指标:DB指数(Davies-Bouldin Index,DBI): D B I = 1 k ∑ i = 1 k max j ≠ i ( a v g ( C i + a v g ( C j ) ) d c e n ( C i , C j ) ) DBI=\frac{1}{k}\sum_{i=1}^k\max_{j\ne i}(\frac{avg(C_i+avg(C_j))}{d_{cen}(C_i,C_j)}) DBI=k1∑i=1kmaxj̸=i(dcen(Ci,Cj)avg(Ci+avg(Cj)))
DBSCAN
ϵ \epsilon ϵ-邻域、核心对象、密度直达、密度可达、密度相连
- 算法过程:
- 给定邻域参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts),找出所有核心对象
- 以任意核心对象出发,有密度可达条件找出聚类蔟,直至所有核心对象均被访问
ROC与AUC
- ROC(Receiver Operating Characteristic,受试者工作特征)
- 横坐标:假正例率 F P F P + T N = F P N \frac{FP}{FP+TN}=\frac{FP}{N} FP+TNFP=NFP,即反例中被预测为正样本的比例
- 纵坐标:真正例率 T P T P + F N = T P P \frac{TP}{TP+FN}=\frac{TP}{P} TP+FNTP=PTP,即正例中被预测为正样本的比例
- AUC(Area Under ROC Curve,ROC曲线下面积)