左倾红黑树（Left-Leaning Red-Black Trees：LLRBT）解析

左倾红黑树（LLRBT）

1.用普通的平衡二叉树（BST）表示2-3-4树

2.用内部的红边表示3-节点和4-节点（红边指入的节点为红节点）

所以我们可以用红黑树来表示2-3-4树。如下：

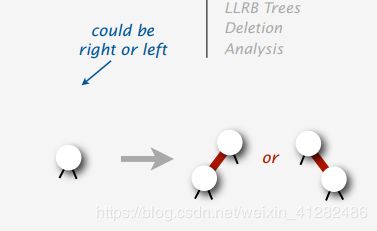
注意：对应关系不是唯一的（3个节点可以任意倾斜），对于一棵2-3-4树可能有多种不同的红黑树表示，这是因为对于3-node的表示，红色的边可以向左倾，也可以向右倾。

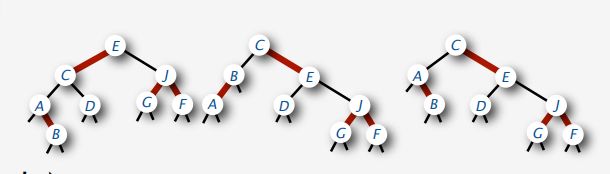
所以要考虑很多情况。但是我们只考虑左倾的情况很大大简化实现。
这种树叫做左倾红黑树。
这样任何一颗2-3-4树都可以得到唯一的左倾红黑树。

以下情况是不允许的：

1.既然是左倾就不能出现右倾3-节点(虽然在标准的红黑树中是允许的，但是这里是左倾红黑树)

2.连续两个红节点（左倾树的原始版本使用此4节点表示形式，但是新版不允许这四种情况出现，如果出现了就要通过旋转调整）

红黑树的查找实现与基本BST相同

BST（和LLRB树）搜索实现：

public Value get(Key key)
{
Node x = root;
while (x != null)
{
int cmp = key.compareTo(x.key);
if (cmp == 0) return x.val;
else if (cmp < 0) x = x.left;
else if (cmp > 0) x = x.right;
}
return null;
}

找一棵树中找最小key

public Key min(){
	Node x = root;
	if(x == null){
		return null;
	}
	if(x.left == null){
		return x.key;
	}
	return min(x.left);
}

左倾红黑树的插入

插入的难点：不仅要插入还要维持红黑颜色。
接下来要介绍以下旋转操作
左旋：

private Node rotateLeft(Node h) {
        // assert (h != null) && isRed(h.right);
        Node x = h.right;
        h.right = x.left;
        x.left = h;
        x.color = x.left.color;
        x.left.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

右旋：

 private Node rotateRight(Node h) {
        // assert (h != null) && isRed(h.left);
        Node x = h.left;
        h.left = x.right;
        x.right = h;
        x.color = x.right.color;
        x.right.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

下面我们来具体分析插入操作
当我们要向红黑树的底部插入一个节点的时候，就可能出现多种情况

如果我们向2-node的节点插入的话，有两种情况，如果插入左孩子，那么直接插入就可以，但如果插入的是右孩子，为了保持左倾，插入之后，我们需要进行一个左旋操作

我们可以看到这种情况对应于2-3-4树就是想2-node插入变成3-node

下面一种情况，就是我们向3-node插入一个节点，那么我们就需要将它变成2-3-4树中对应的树节点
这也是为什么我们之前定义的不允许的情况中的第二种，不允许两条红边连在一起，也就是不允许两个红节点互为父子节点，因为插入的节点一定是红节点。

向3-node插入有三种情况：

向4-node插入：

根据我们之前在2-3-4树中学习的可以知道，我们需要对4-node进行切分，切分的方法就是将4-node的中间节点向上移动到父节点中。

首先，当父节点是2-node时候：

有两种情况

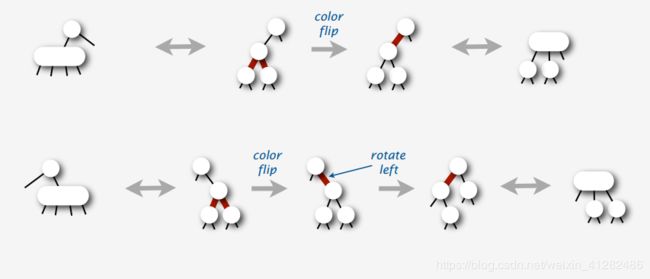
我们发现在红黑树中进行切分工作很简单，只要将两个红节点变成黑，然后父节点变成红就可以了。这个变换的过程，我们叫做 colorflip。

private Node colorFlip(Node h)
{
x.color = !x.color;
x.left.color = !x.left.color;
x.right.color = !x.right.color;
return x;
}

如下图

对于父节点为3-node的情况：

观察这五种情况，我们发现首先都是先进行color flip操作，然后就变成了之前的操作，左旋和右旋。

我们可以把上面这些插入操作总结，然后实现一个统一适用的插入算法

1.在底部插入一个新节点

if (h == null)
return new Node(key, value, RED);

2.分割一个4节点

if (isRed(h.left) && isRed(h.right))
colorFlip(h);

3.强制左倾状态

if (isRed(h.right))
h = rotateLeft(h);

4. Balance a 4-node.
   

if (isRed(h.left) && isRed(h.left.left))
h = rotateRight(h);

完整的插入算法：

private Node put(Node h, Key key, Value val) {
        if (h == null) return new Node(key, val, RED, 1);
	
		if (isRed(h.left)  &&  isRed(h.right))     flipColors(h);
	
        int cmp = key.compareTo(h.key);
        if      (cmp < 0) h.left  = put(h.left,  key, val);
        else if (cmp > 0) h.right = put(h.right, key, val);
        else              h.val   = val;

        // fix-up any right-leaning links
        if (isRed(h.right) && !isRed(h.left))      h = rotateLeft(h);
        if (isRed(h.left)  &&  isRed(h.left.left)) h = rotateRight(h);
        
        h.size = size(h.left) + size(h.right) + 1;

        return h;
    }

如图：

左倾红黑树的删除

1.颜色调整和旋转可保持完美的黑色链接平衡
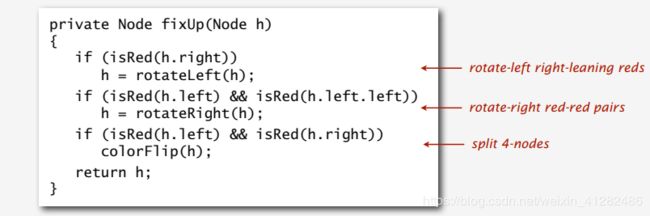
2.向上修复右倾红节点消除4-节点

private Node fixUp(Node h)
{
if (isRed(h.right))
h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left))
h = rotateRight(h);
if (isRed(h.left) && isRed(h.right))
colorFlip(h);
return h;
}

删除策略（适用于2-3和2-3-4树）
•不变量：当前节点不是2节点
•必要时引入4个节点
•从底部取出钥匙
•消除上行中的4个节点

1.删除最大节点

显然最大节点一定是在最右边
如果我们删除的节点在3-node或者4-node中，直接删除掉。

移除2节点会破坏平衡
•在搜索路径的下方变换树
•不变式：当前节点不是2节点

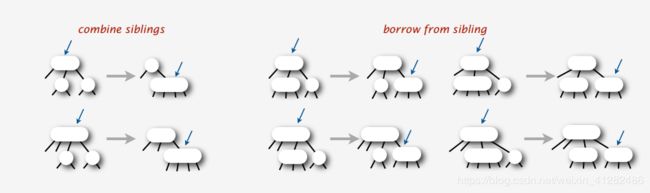
根据父节点的不同。3-node或者4-node和兄弟节点的不同可以分为六种情况，但其中又可以分为两类
第一种处理方法就是兄弟节点不是2-node，就可以直接从兄弟节点借一个节点过来
第二种处理方法兄弟节点是2-node，则从父节点中借一个过来，然后和兄弟节点合并成一个4-node
这六种情况的条件根据2-3-4树转换成红黑树，就是h.right和h.right.left均为黑色。
但其中有需要分为两种
对于上述提到的第二种处理方法，处理比较简单，直接color flip即可

其中这种情况的条件就是左子节点为2-node，也就是h.left.left为黑。

对于h.left.left为红的情况，就对应上述的第一种处理方法，首先color filp，然后还要借一个节点过来

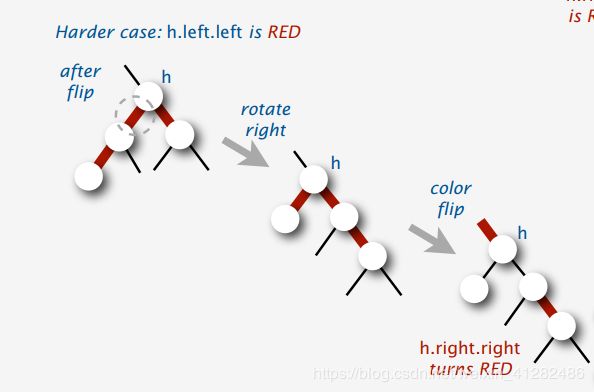
所以将上面两种方法合并：

private Node moveRedRight(Node h)
{
colorFlip(h);
if (isRed(h.left.left))
{
h = rotateRight(h);
colorFlip(h);
}
return h;
}

然后我们就可以得到删除最大节点的算法：

public void deleteMax()
{
	root = deleteMax(root);
	root.color = BLACK;
}
private Node deleteMax(Node h)
{
	if (isRed(h.left))
	h = rotateRight(h);
	if (h.right == null){
		return null;
	}
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
h.right = deleteMax(h.right);
return fixUp(h);
}

流程就是：

首先如果左旋则变为右旋，因为找最大节点在最右边
如果，已经到了最底部，那么直接移除就行，移除的要求是最底部的节点一定是red
如果遇到了2-node就借一个节点
继续往下递归查找
删除完毕，就恢复红黑树
我们下面看两个例子

我们下面看两个例子

2.删除左倾红黑树最小节点

最小节点的方法与最大节点的类似，只不过是从最右边变成了最左边

思想还是一样的

首先，不变量，就是h或者h的left一定是红色的。遇到底部的红节点，就直接删除了。

然后就是对于2-node需要从兄弟节点中借一个节点变成3-node或者4-node
2-node的条件就是，h.left和h.left.left均为黑色的。
然后其中又有两种情况，如果h.right.left为黑，则说明兄弟节点也是2-node，就从父节点借节点，直接color flip即可

如果h.right.left为红，则可以直接从兄弟节点借一个节点过来。

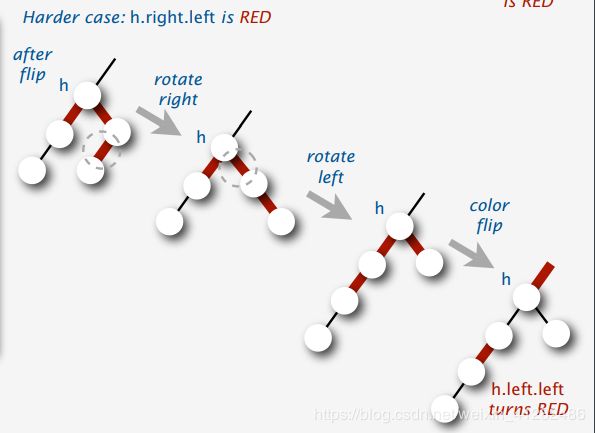
代码是:

private Node moveRedLeft(Node h)
{
colorFlip(h);
if (isRed(h.right.left))
{
h.right = rotateRight(h.right);
h = rotateLeft(h);
colorFlip(h);
}
return h;
}

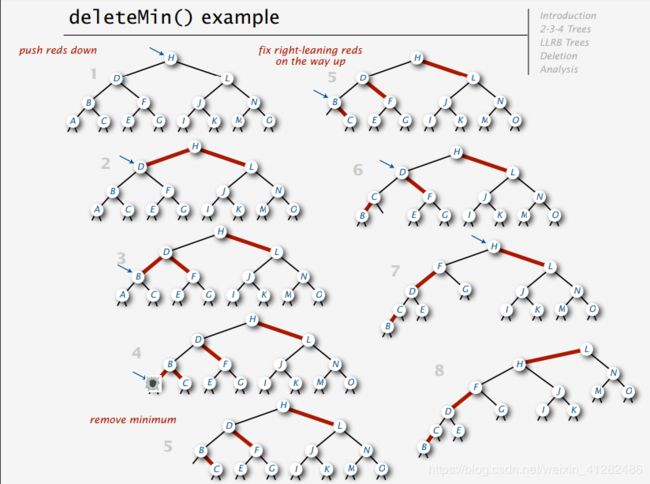
最后归纳得到删除最小节点的代码

public void deleteMin()
{
root = deleteMin(root);
root.color = BLACK;
}
private Node deleteMin(Node h)
{
if (h.left == null)
return null;
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = deleteMin(h.left);
return fixUp(h);
}

如图：

两个删除最小节点的例子：

3.删除任意节点

我们学习了怎么删除最大节点和最小节点，下面我们开始研究最复杂的情况，就是删除任意节点
其实思路是一样的，如果所要删除的节点在3-node或者4-node中，根据2-3-4树的性质直接删除就可以了。
最复杂的情况是如果是2-node，那么删除就会引起不平衡。所以就得从兄弟节点中借一个节点，但由于是任意节点，不像删除最大最小的情况，确定是左边或者右边，而是有很多种情况。

我们变换想法，类似于堆，我们如果要删除一个节点，把要删除的那个节点和最底部的节点交换，然后就变成删除最底部的节点，就可以转换成删除最大节点或者最小节点了。这也就是我们为什么要先讲最大节点和最小节点。同时这样也把问题简化了，因为删除最大和最小节点的方法我们已经分析出来了。

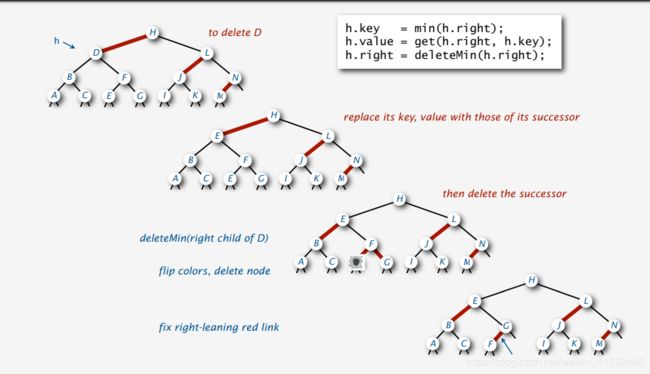
代码如下：

h.key = min(h.right);
h.value = get(h.right, h.key);
h.right = deleteMin(h.right);

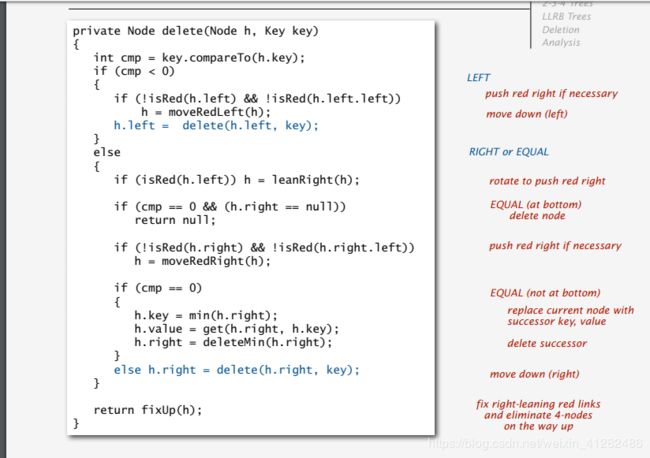
红黑树删除任意节点的代码：

private Node delete(Node h, Key key)
{
int cmp = key.compareTo(h.key);
if (cmp < 0)
{
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = delete(h.left, key);
}
else
{
if (isRed(h.left)) h = leanRight(h);
if (cmp == 0 && (h.right == null))
return null;
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
if (cmp == 0)
{
h.key = min(h.right);
h.value = get(h.right, h.key);
h.right = deleteMin(h.right);
}
else h.right = delete(h.right, key);
}
return fixUp(h);
}

如图：