吴恩达机器学习课后习题ex5偏差与方差（python实现）

实现

在前半部分的练习中，你将实现正则化线性回归，以预测水库中的水位变化，从而预测大坝流出的水量。在下半部分中，您将通过一些调试学习算法的诊断，并检查偏差 v.s. 方差的影响。

import numpy as mp
import pandas as pd
import matplotlib .pyplot as plt
from scipy.io import loadmat
data=loadmat('ex5data1.mat')
data

数据被分为训练集、验证集和测试集。
训练集用来训练，验证集用来进行模型（参数）的选择，测试集用来看模型的泛化能力。

X=data['X'] #(12,1)
y=data['y'] 
X_val=data['Xval'] #(21,1)
y_val=data['yval']
X_test=data['Xtest'] #(21,1)
y_test=data['ytest']
X=np.insert(X,0,1,axis=1)
X_val=np.insert(X_val,0,1,axis=1)
X_test=np.insert(X_test,0,1,axis=1)
#作图观察
fig,ax=plt.subplots(figsize(12,8))
ax.scatter(data['X'],data['y'],label='training data')
ax.set_xlabel('change in water level x')
ax.set_ylabel('water flowing out of the dam y')
plt.show()

使用一个正则化线性回归函数来拟合它

def reg_cost(theta,X,y,lambd):
  error=X@theta-y.flatten()
  first=np.sum(np.power(error,2))
  reg=lambd*(np.power(theta[1:],2))
  return first+reg/(2*len(X))
def reg_gradient(theta,X,y,lambd):
  error=X@theta-y.flatten()
  first=(X.T@error)/len(X)
  reg=(lambd/len(X))*theta
  reg[0]=0
  return first+reg

from scipy.optimize import minimize
def train(X,y,lambd):
  theta=np.ones(X.shape[1])
  res=minimize(fun=reg_cost,x0=theta,args=(X,y,lambd),method='TNC',jac=reg_gradient)
  return res.x

theta_final=train(X,y,lambd=0)
theta_final

array([13.08790348, 0.36777923])
画出拟合曲线

x=np.linspace(-50,50,100)
f=theta_final[0]+theta_final[1]*x
fig,ax=plt.subplots(figsize(12,8))
ax.scatter(data['X'],data['y'],label='training data')
ax.plot(x,f,'r')
ax.set_xlabel('change in water level x')
ax.set_ylabel('water flowing out of the dam y')
plt.show()

从图中可以看出，存在欠拟合的状态，bisa偏差很大。

画出训练集和验证集的学习曲线来观察偏差、方差情况

训练样本X从1开始逐渐增加，训练出不同的参数向量θ。接着通过交叉验证样本Xval计算验证误差。

1、使用训练集的子集来训练模型，得到不同的theta。
2、通过theta计算训练代价和交叉验证代价，切记此时不要使用正则化，将 λ=0。
3、计算交叉验证代价时记得整个交叉验证集来计算，无需分为子集。

def plot_learningcurve(X,y,X_val,y_val,lambd):
  x=range(1,X.shape[0]+1)
  traingcosts=[]
  valcosts=[]
  for i in x:
    theta_s=train(X[:i,:],y[:i,:],lambd)
    traingcost=reg_cost(theta_s,X[:i,:],y[:i,:],lambd)
    valcost=reg_cost(theta_s,X_val,y_val,lambd)
    traingcosts.append(traingcost)
    valcosts.append(valcost)

  plt.plot(x,traingcosts,label='trainging cost')
  plt.plot(x,valcosts,label='val cost')
  plt.legend()
  plt.xlabel('number of training examples')
  plt.ylabel('error')
  plt.show()

lambd=0
plot_learningcurve(X,y,X_val,y_val,lambd)

随着训练集增大后，误差不再有太大的改观，高偏差问题。

对于高偏差问题，可以采取：
1、采用多项式特征
2、减小正则化参数
这里我们采用增加多项式特征
$y={\theta }_0+{\theta }_1\ast x+{\theta }_2\ast x^2+...+{\theta }_n\ast x^n$

def feature(X,power):
  for i in range(2,power+1):
    X=np.insert(X,X.shape[1],np.power(X[:,1],power),axis=1)
  return X

为了防止特征的量纲不一致，对x进行归一化

不同特征具有不同量级时会导致：a.数量级的差异将导致数量级大的特征占据主导地位；b.数量级的差异将导致迭代收敛速度变慢。

关于归一化，所有数据集应该都用训练集的均值和样本标准差处理！！！否则数据分布不一致，具体可以参考https://www.zhihu.com/question/312639136

def get_mean_std(X):
  means=np.mean(X,axis=0) #按列求均值 (1,power+1)
  stds=np.std(X,axis=0)  #(1,7)
  return means,stds

def feature_normalize(X,means,stds):
  
  X[:,1:]=(X[:,1:]-means[1:])/stds[1:]
  return X

power=6
X_poly=feature(X,power)
X_val_poly=feature(X_val,power)
X_test_poly=feature(X_test,power)
train_means,train_stds=get_mean_std(X_poly)
train_means,train_stds

从train_means,train_stds的值我们可以知道为什么feature_normalize要去掉第一列，否则会遇到(1-1)/0

RuntimeWarning: invalid value encountered in true_divide

X_norm=feature_normalize(X_poly,means,stds)
X_val_norm=feature_normalize(X_val_poly,means,stds)
X_test_norm=feature_normalize(X_test_poly,means,stds)
theta_fit=train(X_norm,y,lambd=0)

#画拟合曲线
def plot_ploy_fit():
  x=np.linspace(-50,50,100)
  xx=x.reshape(100,1)
  xx=np.insert(xx,0,1,axis=1)
  xx=feature(xx,power)
  xx=feature_normalize(xx,train_means,train_stds)
  fig, ax = plt.subplots(figsize=(12,8))
  ax.scatter(data['X'], data['y'], label='Traning Data')
  ax.plot(x,xx@theta_fit,'r--')
  ax.set_xlabel('Change in water level x')
  ax.set_ylabel('Water flowing out of the dam y')
  plt.show()

plot_poly_fit()

#调用学习曲线函数
plot_learningcurve(X_norm,y,X_val_norm,y_val,lambd=0)

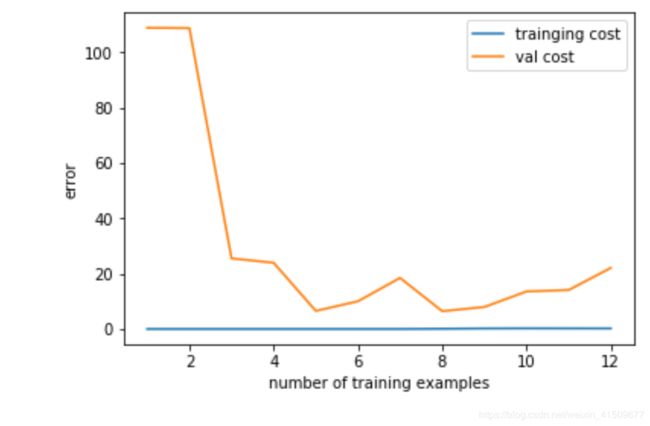
从图中可以看出，训练集误差为0，验证集误差仍然比较大，处于过拟合状态。
可以通过选择合适的lambd的值来改善欠拟合

lambds=[0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
training_cost=[]
cv_cost=[]
for lambd in lambds:
  theta=train(X_norm,y,lambd) #计算对应的theta值
  #计算代价函数时，不需要lambd
  tc=reg_cost(theta,X_norm,y,lambd=0)
  cv=reg_cost(theta,X_val_norm,y,lambd=0)
  training_cost.append(tc)
  cv_cost.append(cv)

plt.plot(lambds,training_cost,label='trainingcost')
plt.plot(lambds,cv_cost,label='cvcost')
plt.show()

从图中可以看出，当lambd=3时，cvcost最小。

i=np.argmin(cv_cost)  #i=8
lambds[i]

结果是3
计算得到的模型在测试集上的代价函数值

res=train(X_norm,y,lambd=3)
cost=reg_cost(res.x,X_test_norm,y_test,lambd=0)
print(cost)

结果是4.3976161577441975